Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła matematycznego
Wahadłem matematycznym nazywamy punkt masowy zaczepiony na nieważkiej nici. Dla małego wychylenia można przyjąć, iż wahadło matematyczne porusza się ruchem harmonicznym. Wtedy jego okres opisujemy wzorem
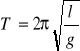
gdzie l - długość nici. Stąd:
![]()
Dla zwiększenia dokładności mierzymy czas dziesięciu okresów.
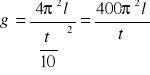
W doświadczeniu użyjemy kulki żelaznej zawieszonej na lekkiej żyłce, co w przybliżeniu odpowiada wahadłu matematycznemu.
Dokładność pomiaru długości wahadła wynosi Δl = 0,001 [m], a dokładność pomiaru czasu wynosi Δt = 0,001 [s].
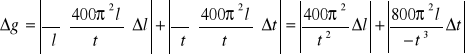
|
l [m] |
t = 10 T [s] |
g [m/s2] |
Δg [m/s2] |
1 |
0,50 |
14,131 |
9,8754 |
0,02322 |
2 |
0,45 |
13,298 |
10,0364 |
0,02609 |
3 |
0,40 |
12,692 |
9,7934 |
0,03439 |
4 |
0,30 |
10,869 |
10,01567 |
0,02395 |
Policzmy wartość średnią g:
![]()
Następnie liczymy odchylenie standardowe stosując współczynnik Studenta - Fishera dla 4 prób tn=1,3:
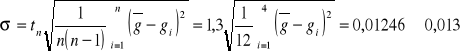
Ostatecznie, po zaokrągleniu: g = 9,96± 0,013 [m/s2]
Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
Wahadło fizyczne - każde ciało sztywne mogące się wahać wokół osi poziomej. Po wychyleniu z położenia równowagi na ciało działa moment siły ciężkości . Stosując do tej sytuacji II zasadę dynamiki Newtona otrzymujemy równanie:
gdzie: oznacza moment bezwładności ciała względem punktu zawieszenia, - kąt wychylenia od położenia równowagi, - odległość od punktu zawieszenia do środka ciężkości wahadła. Ujemna wartość wyrażenia wskazuje, że moment siły dąży do zmniejszenia wychylenia ciała od punktu równowagi.
Z równania wynika, że przyspieszenie kątowe jest proporcjonalne do sinusa kąta wychylenia, a nie do samego kąta, więc ruch wahadła nie jest ruchem harmonicznym. Jeżeli ograniczymy się do małych wychyleń, to![]()
![]()
Porównując to z ogólnym równaniem ruchu harmonicznego otrzymujemy:
gdzie - prędkość kątowa.
Przyrównując powyższe wzory otrzymujemy wzór na okres drgań wahadła fizycznego:
Mając dane wahadło matematyczne i fizyczne możemy dobrać długość pierwszego, aby okresy drgań obu wahadeł były równe. W ten sposób otrzymujemy długość zredukowaną wahadła fizycznego. Jest ona równa długości posiadającego taki sam okres wahadła matematycznego. Jeżeli znamy długość zredukowaną wahadła fizycznego, wtedy jego okres drgań możemy znaleźć z równania:
Do wyznaczenia długości zredukowanej wykorzystujemy własność wahadła fizycznego: Wahadło zawieszone w punkcie A, a następnie w punkcie B posiada taki sam okres, jeżeli odległość między punktami zawieszenia jest długością zredukowaną. Aby dowieść słuszności twierdzenia wystarczy wyznaczyć warunki równości okresów i dla dowolnej odległości między punktami A i B.
Specjalną postacią wahadła fizycznego ułatwiającą wyznaczenie długości zredukowanej, jest wahadło rewersyjne lub odwracalne. Na długim pręcie znajdują się dwa ciężarki, które mogą być przesuwane wzdłuż pręta. Osie obrotu A i B znajdują się przy przeciwnych końcach pręta.
Mocując jeden ciężarek na stałe i zmieniając położenie drugiego, zmieniamy moment bezwładności wahadła. Pozwala nam to dobrać moment bezwładności, by odległość między punktami A i B była długością zredukowaną, a następnie obliczyć przyspieszenie ziemskie według wzoru:
![]()
Dla zwiększenia dokładności pomiaru mierzymy czas równy 10 okresom: t = 10T
ls - odległość ciężarka jego położenia przy pomiarze 1.
L.p. |
ls [m] |
tA=10 TA [s] |
tB=10 TB [s] |
1 |
1 |
19,7537 |
20,202 |
2 |
0,9 |
19,3517 |
19,4613 |
3 |
0,8 |
19,093 |
18,8643 |
4 |
0,7 |
18,9747 |
18,4003 |
5 |
0,6 |
18,9853 |
18,1763 |
6 |
0,5 |
19,0897 |
18,3997 |
7 |
0,4 |
19,2827 |
19,4737 |
Punkt przecięcia krzywych: t = 19,3 [s]
![]()
![]()
Przyjmujemy dokładności pomiarów: Δl = 0,02 [m] i Δt = 0,001 [s]
Porównanie wyników
ćwiczenie |
g [m/s2] |
Δg [m/s2] |
wahadło matematyczne |
9,96 |
0,013 |
wahadło rewersyjne |
9,8 |
0,2 |
wartość z tablic |
9,80665 |
- |
Wnioski:
Wyniki obu pomiarów z błędami są zgodne z wartością z tablic.
W przypadku wahadła rewersyjnego błąd jest trudny do oszacowania, gdyż nie wiadomo jak na niego wpłynęło zastosowanie ekstrapolacji.
Wpływ na dokładność pomiaru przyspieszenia za pomocą wahadła rewersyjnego ma duża niedokładność miary wyskalowanej na pręcie.
Wyniki obu pomiarów znacznie polepsza dokładne urządzenie mierzące okres.
Podsumowując - dokładniejszy wynik uzyskuje się za pomocą wahadła matematycznego.
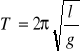
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Lab fiz 302, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
Lab fiz 104, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
Lab fiz 206, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
Lab fiz 303, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
204pl, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 prac
teoria do 109, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria
Ćw109mmm, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 p
302, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z 1 pracow
Tabelka 303, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
305przyklad, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, wszystkie laboratoria z
lab 1, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza
206e, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka -
104, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka -
104e, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka -
100, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fizyka -
więcej podobnych podstron