Rozwi─ůzanie zestawu E:
Zadanie 1:
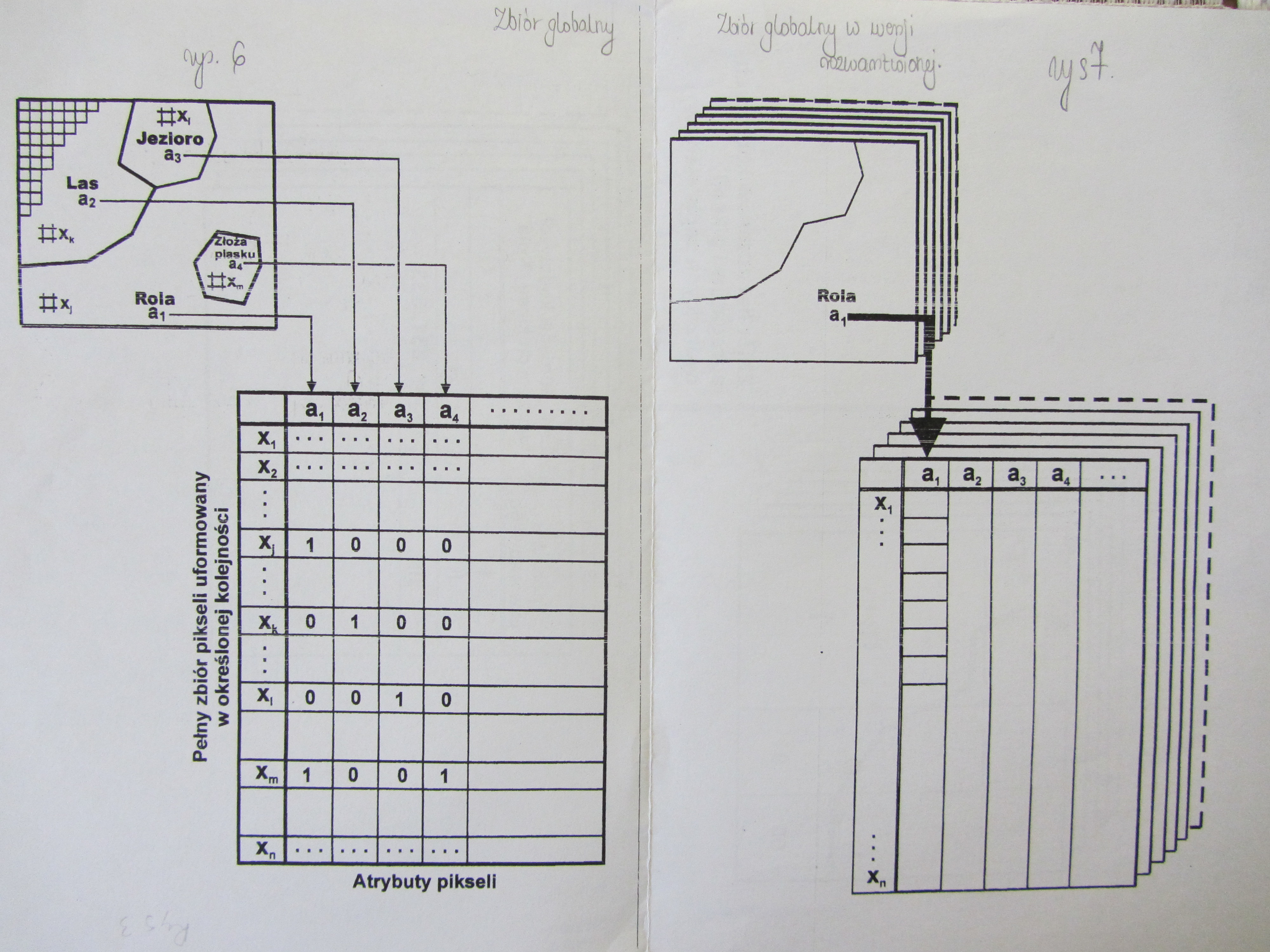
Rastrowy zbi├│r globalny
Model rastrowy (mozaikowy). - ziarniste widzenie przestrzeni, polega na arbitralnym podzieleniu obrazu na ma┼ée elementy - piksele. Dzielenie to nazywamy teselacj─ů.
1.Zbi├│r globalny
Je┼╝eli na obraz mapy na┼éo┼╝ymy siatk─Ö rastra to wszystkie obiekty wyra┼╝one b─Öd─ů za pomoc─ů piksela.
Struktura i cechy zbioru globalnego:
Zbi├│r globalny ma struktur─Ö tablicy. Ma tyle wierszy ile jest pikseli. Ma tyle kolumn ile jest atrybut├│w.
Wymiar tej tablicy jest bardzo du┼╝y. Cechy dla pojedynczego piksela mog─ů si─Ö powtarza─ç. Zbi├│r globalny jest zbiorem binarnym a w rzeczywisto┼Ťci mo┼╝e zawiera─ç dowolne warto┼Ťci (kolory, barwy). Zbi├│r globalny jest zbiorem kompletnym. Zapisuje ca┼éy przegl─ůd sytuacji. Przyjmuje ┼╝e co┼Ť istnieje albo nie. Mo┼╝emy wpisywa─ç warto┼Ť─ç dowolnych dziedzin.
Jest uniwersalnym zapisem. Wady: jest
bardzo du┼╝y, jest nieoszcz─Ödny, musimy go selekcjonowa─ç.
Zaleta: pe┼ény zapis ┼Ťwiata realnego (┼╝eby wygenerowa─ç warstw─Ö trzeba przeprowadzi─ç selekcj─Ö).
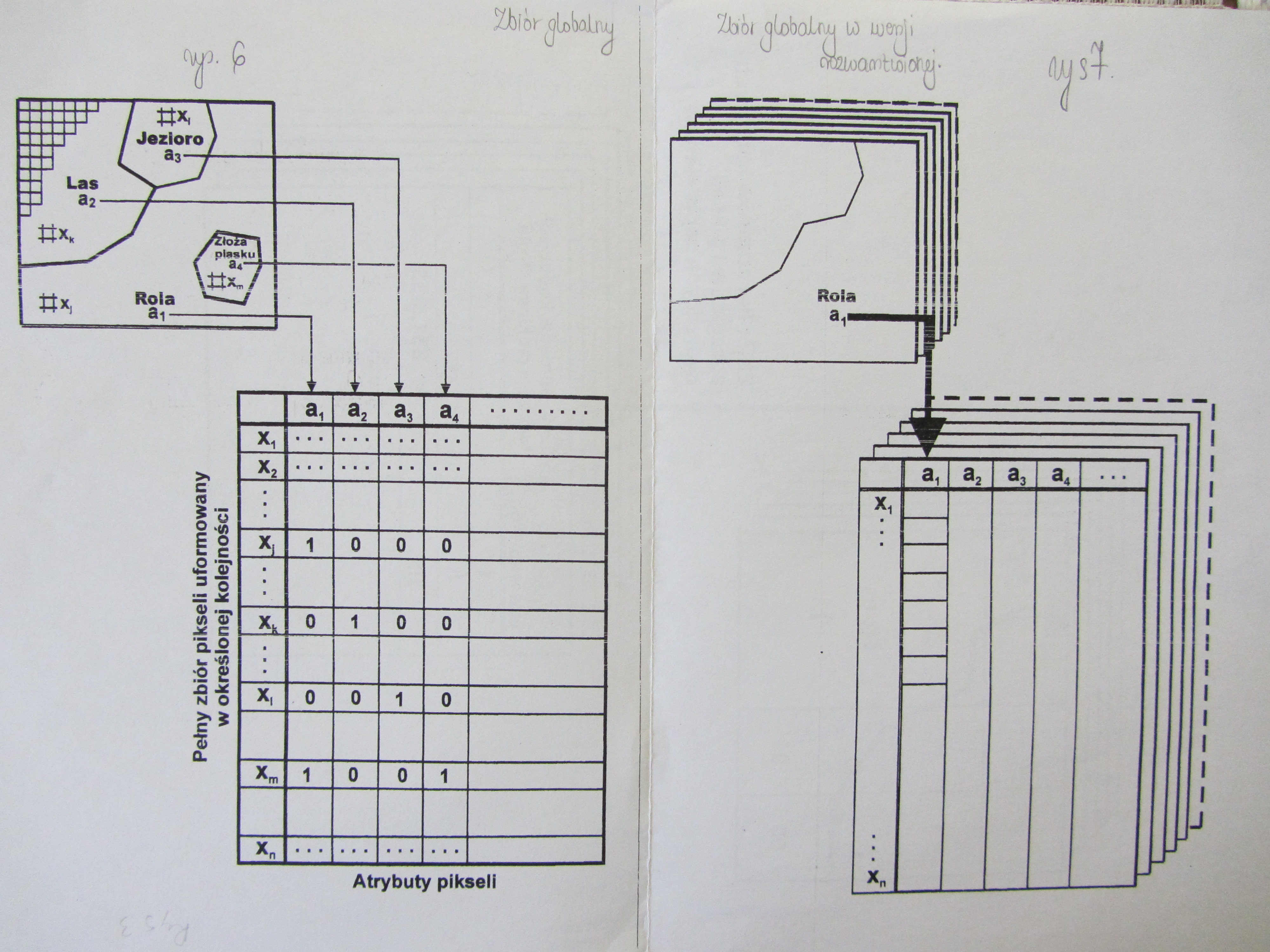
2.Zbi├│r globalny w wersji rozwarstwionej- zbi├│r tablic
(ka┼╝da kolejna tablica to kolejny atrybut.) Z jednej tablicy powstaje tyle tablic ile atrybut├│w. Nadal ma du┼╝o zer. Generowanie zestaw├│w tematycznych musi by─ç zawi─ůzane z selekcja. Zbiory warstw tematycznych zespalaj─ů potrzeby generowania zestawie┼ä tematycznych. Takie zbiory powinny by─ç kompresowane.
Kompresja obrazu- pozbycie si─Ö zer:
Pocz─ůtkowy + liczba powt├│rze┼ä
Pocz─ůtkowy + ko┼äcowy i co tam jest
Zbi├│r globalny w wersji rozwarstwionej jest w dalszym ci─ůgu wielki i nieoszcz─Ödny, dlatego te┼╝ powsta┼é trzeci spos├│b zapisu.
3.Zbiory warstwy tematycznej w oparciu o hierarchiczne rozwini─Öcie obrazu
Sporz─ůdza list─Ö agregat├│w (blok) kt├│re ca┼ékowicie mieszcz─ů si─Ö w danych obiektach od najwi─Ökszego do najmniejszego agregatu - wynikiem jest lista kod├│w agregat├│w, kt├│re nie dziel─ů si─Ö dalej bo kolejne elementy maj─ů takie same atrybuty
┼╗eby zbudowa─ç ka┼╝d─ů klas─Ö musimy sporz─ůdzi─ç list─Ö kod├│w drzewa czw├│rkowego. Podzia┼é przestrzeni jest wi─Öc zgodny z drzewem czw├│rkowym, a zbi├│r warstw tematycznych ma struktur─Ö listy.
|
|
|
|||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
|
|
|
|||
Kolejno┼Ť─ç narastania kod├│w w schemacie drzewa czw├│rkowego pokrywa si─Ö z kierunkiem przebiegania zgodnym z lini─ů Peana.
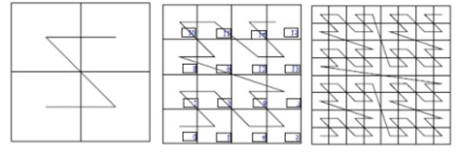
linia fraktalna Peana umo┼╝liwia budow─Ö zwi─ůzk├│w hierarchicznych (blok├│w pikseli), dalsze stopnie o identycznym kszta┼écie, wykonuje kr├│tkie przebiegi w lokalnej przestrzeni, oscyluje w lokalnej przestrzeni, minimalna liczba skok├│w. Niezmiernie oszcz─Ödny zapis.
Ka┼╝dy kolejny powstaje z 4 poprzednich
Zalety: - oszcz─Ödny zapis przy u┼╝yciu stopni podzia┼éu. - obszar reprezentowany przez max agregaty -regularno┼Ť─ç -┼éatwo┼Ť─ç zamiany na wsp├│┼érz─Ödne -pola b─Öd─ůce s─ůsiadami maj─ů podobne kody, -hierarchiczna struktura, -wy┼╝szy stopie┼ä organizacji.
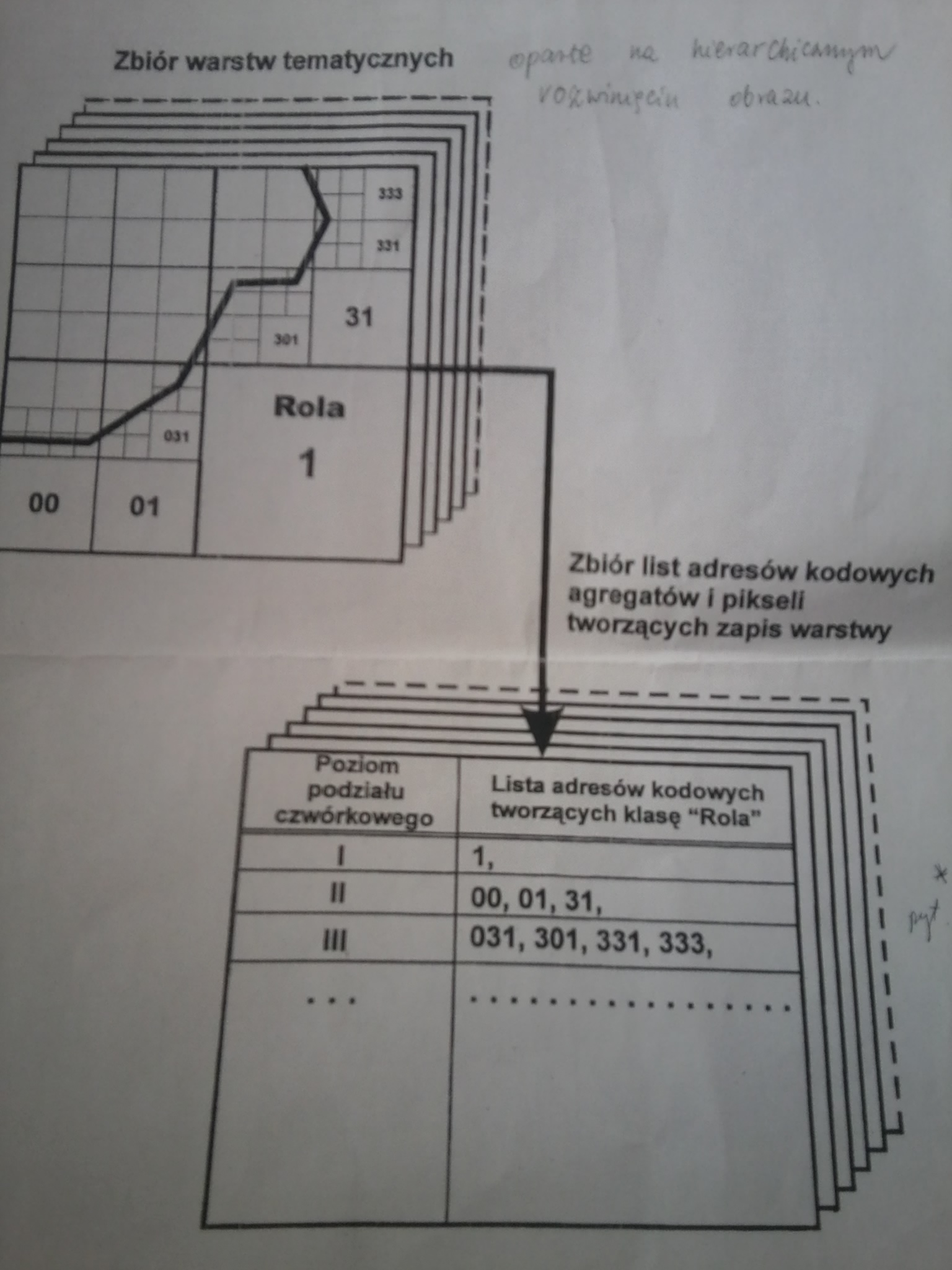
Opis przebiegu zapisu warstwy:
Poszukujemy pe┼énych agregat├│w, rejestrujemy kolejne maksymalne agregaty na poszczeg├│lnych poziomach podzia┼éu, kt├│re mieszcz─ů si─Ö ca┼ékowicie w konturach obiektu danej klasy. Kody tych agregat├│w zapisujemy w postaci listy. Takie agregaty nie podlegaj─ů ju┼╝ dalszemu podzia┼éowi, poniewa┼╝ posiadaj─ů ten sam atrybut. To daje znaczn─ů oszcz─Ödno┼Ť─ç zapisu, poniewa┼╝ du┼╝e obszary s─ů reprezentowane przez agregaty o maksymalnej wielko┼Ťci. W miar─Ö dopasowywania si─Ö granic obiektu, tworzymy zapis coraz mniejszych agregat├│w. Lista si─Ö powi─Öksza ale i tak ten zapis jest o wiele bardziej oszcz─Ödny, ni┼╝ zbi├│r globalny lub zbi├│r globalny w wersji rozwarstwionej.
Zadanie 2:
Spos├│b (model rastrowy) - model w kt├│rym zapis przestrzeni 2D jest ukierunkowany na elementy sk┼éadowe obrazu - regularna siatka p├│l elementarnych jest rozwijana do postaci liniowej, a z chwil─ů uformowania siatki p├│l (zwanej rastrem) ka┼╝dy obraz mo┼╝e by─ç wyra┼╝ony wy┼é─ůcznie poprzez geometri─Ö element├│w siatki;
Wyb├│r sposob├│w przebiegania:
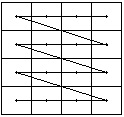
a) wierszowe-
du┼╝e skoki
i wiele skok├│w
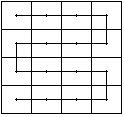
b) serpentynowy
-eliminuje skoki
ale zaburza kolejno┼Ť─ç
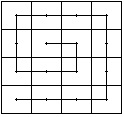
c)spiralny-usuwa skoki, jest zawsze
w tych samych kierunkach, s─ů tu
martwe przebiegi, została
wprowadzona asymetria: g─Östo┼Ť─ç
przebiegania na zewn─ůtrz jest inna
ni┼╝ g─Östo┼Ť─ç w ┼Ťrodku.
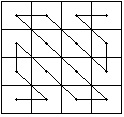
d)diagonalny Cantora (usuwa skoki ale zaburza kolejno┼Ť─ç,
wprowadza dezintegracj─Ö,
s─ů tu martwe przebiegi,
s─ů du┼╝e przebiegi).
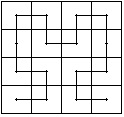
sposoby hierarchiczne:
e) przebieganie Hilberta-kierunek umo┼╝liwia
budow─Ö zwi─ůzk├│w hierarchicznych, oscyluje
w lokalnej przestrzeni, symetryczny
wzgl─Ödem linii p┼én-p┼éd, wad─ů jest to ┼╝e
hierarchia jest oparta o obracanie o 90O
f) linia fraktalna Peana-umo┼╝liwia budow─Ö zwi─ůzk├│w hierarchicznych (blok├│w pikseli), dalsze stopnie o identycznym kszta┼écie, wykonuje kr├│tkie przebiegi w lokalnej przestrzeni, oscyluje w lokalnej przestrzeni, minimalna liczba skok├│w. Niezmiernie oszcz─Ödny zapis.
Ka┼╝dy kolejny powstaje z 4 poprzednich
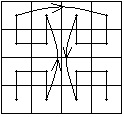
g)kody Gray'a- eliminuje
duże błędy, symetryczny
w kierunku linii płn-płd
Zadanie 3:
Nieregularna sie─ç tr├│jk─ůt├│w powstaje g┼éownie jako efekt bezpo┼Ťrednich pomiar├│w terenowych, gdzie ca┼éy zakres opracowania zape┼énia si─Ö tr├│jk─ůtami opartymi o punkty pomiarowe. Poniewa┼╝ w tych modelach wykorzystywane s─ů wszystkie punkty charakterystyczne model jest stosunkowo dok┼éadny.
a) triangulacja Delaunay'a
Tr├│jk─ůty tworzone s─ů w ten spos├│b aby ┼╝aden z punkt├│w nie nale┼╝─ůcych do niego nie by┼é
po┼éo┼╝ony wewn─ůtrz okr─Ögu opisanego na tr├│jk─ůcie
b) Obszar Thiessena stanowi zbi├│r wszystkich punkt├│w p┼éaszczyzny, dla kt├│rych odleg┼éo┼Ť─ç do punktu centralnego jest mniejsza od odleg┼éo┼Ťci do pozosta┼éychpunkt├│w. Ograniczenia tego obszaru stanowi─ů odcinki symetralnych do bok├│w triangulacji Delaunay'a.
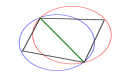
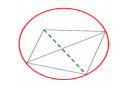
Triangulacja Delaunaya maksymalizuje warto┼Ť─ç minimalnego k─ůta w tr├│jk─ůcie.( z spo┼Ťr├│d wszystkich wyselekcjonowanych punkt├│w w kole do polaczenia pkt centralny zostanie polaczony z tymi punktami kt├│rych symetralne utworzy┼éy wielobok thiessen
Najcz─Ö┼Ťciej stosowany jest algorytm Delaunay'a w kt├│rym wykorzystywane s─ů poligony Thiessena. Triangulacja powinna by─ç tak wykonana ┼╝eby: - tworzone tr├│jk─ůty by┼éy mo┼╝liwie zbli┼╝one do r├│wnobocznych i mo┼╝liwie ma┼ée; - ka┼╝dy punkt ze zbioru punkt├│w rozproszonych musi by─ç uwzgl─Ödniony; -procedura post─Öpowania musi by─ç jednoznaczn─ů
Gdy nie s─ů znane sposoby po┼é─ůczenia punkt├│w stosuje sie triangulacje Delaunay'a z wykorzystaniem wielobok├│w Thiessena (mamy jak po┼é─ůczy─ç punkty rozproszone)
-tr├│jk─ůty zbli┼╝one do r├│wnobocznych
-ka┼╝dy punkt musi by─ç wykorzystany
-procedura musi by─ç jednoznaczna
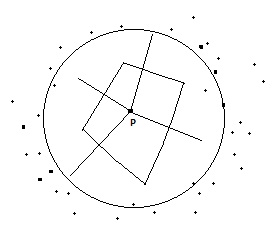
Przebieg tworzenia:
1. obieramy jak─ů┼Ť odleg┼éo┼Ť─ç R, r├│wn─ů lub wi─Öksz─ů ni┼╝ ┼Ťrednia odl mi─Ödzy pkt
2. zakre┼Ťlamy okr─ůg o promieniu R na ka┼╝dym punkcie, w tym okr─Ögu znajda si─Ö punkty kandyduj─ůce do po┼é─ůczenia z tym punktem.
3. ┼é─ůczymy pkt P ze wszystkimi punktami kandyduj─ůcymi i kre┼Ťlimy symetralne tych odcink├│w
4. Z tych symetralnych budujemy najmniejszy wielobok. wielobok ten to wielobok Thiessena. Ka┼╝dy punkt zawarty wewn─ůtrz tego wieloboku jest bli┼╝ej punktu P ni┼╝ innego punktu.
5. Spo┼Ťr├│d wszystkich pkt wyselekcjonowanych w okr─Ögu punkt P b─Ödzie po┼é─ůczony tylko z tymi punktami, kt├│rych symetralne utworzy┼éy wielobok Thissena, te pkt b─Öd─ů tworzy┼éy fragment przysz┼éej siatki.
6. Resztę punktów które nie utworzyły wieloboku się odrzuca.
7. Powy┼╝sza procedura powtarza si─Ö dalej dla wszystkich punkt├│w rozproszonych
Matematycznie: budujemy ostrosłup i zakładamy, że V=0
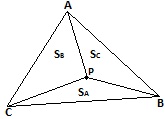
Wysoko┼Ť─ç punktu P jest ┼Ťredni─ů wa┼╝on─ů z wysoko┼Ťci trzech punkt├│w, gdzie wagami s─ů pola tr├│jk─ůt├│w le┼╝─ůcych naprzeciwko.
Zadanie 4:
4.1). S=(PRACOWNICY [NAZWISKOPRAC] + STUDENCI [NAZWISKOSTUD]) x LISTACZYTELN [NAZWISKOCZYT]
Komentarz: Najpierw musimy wykona─ç dwie projekcje: tabeli PRACOWNICY, tak aby pozosta┼é jedynie atrybut z nazwiskiem pracownika (NAZWISKOPRAC), oraz tabeli STUDENCI, tak aby pozosta┼é atrybut z nazwiskiem studenta (NAZWISKOSTUD). Projekcja jest to przekszta┼écenie usuwaj─ůce r├│┼╝norodno┼Ťci, jest skre┼Ťlaniem atrybut├│w i wybieraniem tylko tych, kt├│re nas interesuj─ů. Nast─Öpnie przetworzone tablice po projekcji dodajemy do siebie. Dodawanie daje w wyniku relacje zawieraj─ůce wszystkie krotki, a powt├│rzenia s─ů usuwane. W dodawaniu wszystkie operanty musz─ů mie─ç takie same atrybuty, dlatego wykonano projekcj─Ö, aby obie dodawane tablice mia┼éy takie same atrybuty NAZWISKO. Niewa┼╝ne tu jest, ┼╝e nag┼é├│wki s─ů r├│┼╝ne (NAZWISKOPRAC i NAZWISKOSTUD), mo┼╝emy wykonywa─ç operacje na tych tablicach relacji, poniewa┼╝ maj─ů atrybuty tego samego typu (nazwisko). Kolejnym krokiem by┼éo wykonanie projekcji tabeli LISTACZYTELN, tak aby pozosta┼é tylko atrybut z nazwiskiem (NAZWISKOCZYT). Na koniec wykonano mno┼╝enie pomi─Ödzy wynikow─ů tabel─ů z dodawania i wynikow─ů tabel─ů po projekcji. By┼éo to mo┼╝liwe, poniewa┼╝ posiada┼éy one takie same atrybuty. Wynikiem mno┼╝enia jest obszar wsp├│lny - krotki, kt├│re wyst─Öpuj─ů jednocze┼Ťnie w obu relacjach. Jako wynik otrzymali┼Ťmy nazwiska student├│w i pracownik├│w, kt├│rzy cho─ç raz w tym semestrze byli w czytelni.
4.2). S={(PRACOWNICY + STUDENCI) / LISTACZYTELN} [NAZWISKO]
Komentarz: Logiczne jest, ┼╝e b─Ödziemy te nazwiska poszukiwa─ç na og├│lnych listach nazwisk PRACOWNICY i STUDENCI. Musimy wi─Öc stworzy─ç tak─ů zsumowan─ů list─Ö, a p├│┼║niej wykre┼Ťli─ç z niej te nazwiska, kt├│re wyst─Öpuj─ů w zbiorze czytelnik├│w: LISTACZYTELN. Aby tego dokona─ç, najpierw wykonujemy dodawanie dw├│ch tablic relacji: PRACOWNICY i STUDENCI, a nast─Öpnie od tablicy wynikowej odejmujemy list─Ö czytelnik├│w (LISTACZYTELN), aby dowiedzie─ç si─Ö kogo na tej li┼Ťcie nie by┼éo. Musimy w tym przypadku by─ç bardzo ostro┼╝ni i nie wykonywa─ç projekcji wcze┼Ťniej, tylko na samym ko┼äcu, poniewa┼╝ gdy w dzia┼éaniach na tablicach relacji wyst─Öpuje odejmowanie, to nie mo┼╝emy robi─ç wcze┼Ťniej projekcji, bo to zlikwidowa┼éoby r├│┼╝norodno┼Ť─ç. Dlatego te┼╝ ostatnim krokiem by┼éo wykonanie projekcji wzgl─Ödem NAZWISKA (mimo i┼╝ nag┼é├│wki w ka┼╝dej z tablic by┼éy r├│┼╝ne NAZWISKOSTUD, -PRAC, -CZYT, to dzia┼éania na tych tablicach by┼éy mo┼╝liwe, poniewa┼╝ atrybuty by┼éy takie same). W wyniku otrzymali┼Ťmy tabel─Ö z nazwiskami student├│w i pracownik├│w, kt├│rzy w tym semestrze ani razu nie byli w czytelni.
Wyszukiwarka
Podobne podstrony:
Zadania-rozwiazane zestaw6
Rozwi─ůzanie zestawu D
Rozwi─ůzanie zestawu C
Chemia ─ćwiczenia zestawy rozwi─ůzane, Zestaw nr 7 rozwiazany, Zestaw 7
Rozwi─ůzanie zestawu E
Rozwi─ůzane zestawy Viola Milas
rozwi─ůzania zestawu 8,9
Matematyka Zestaw 2 Rozwi─ůzany
zestaw B, C rozwiazane (2)
zestaw 07 rozwiazania
Zestaw1 PR rozwiazania id 58873 Nieznany
planimetria zestawy 13 i 14 rozwi─ůzane- Aksjomat Toru─╣ÔÇ×
wi─Öcej podobnych podstron