Zestaw C:

Zadanie 1:

Zbiór segmentów można traktować jako jedną strukturę: ŁAŃCUCH. Łańcuch posiada następujące cechy: -oznaczenie Li, -rozpoczyna się i kończy w węźle, -ma kierunek wyznaczony przez węzeł początkowy i końcowy, -pomiędzy węzłem początkowym a końcowym łańcuch ma dowolną liczbę punktów pośrednich, które nadają mu kształt, -na całej swojej rozciągłości łańcuch posiada niezmienny obszar po lewej stronie i po prawej stronie. Topologia obszarów w modelu łańcuchowym polega na zestawieniu obszarów uporządkowanej listy łańcuchów, który ten obszar tworzą. Przebiegamy te łańcuchy tak, żeby ten obszar był po prawej stronie.

Oznaczenie obszaru	Uporządkowana lista łańcuchów tworzących obszar
P1 (łąka)	+L1, +L4, +L6, +L3
P2 (las)	+L5, -L4, -L2, -L3
P3 (woda)	-L6, -L5, Ǿ, +L7, -L8
P4 (zamek)	+L8, -L7, Ǿ, -L9
P5 (dziedziniec)	+L9
P0 (nieskończona przestrzeń)	+L2, -L1

Znak Ǿ oznacza, że jest to obszar z wyspą wewnętrzną, która również musi zostać ujęta po tym właśnie znaku. ZASADA KONTROLI: każdy łańcuch występuje dwukrotnie, ale z przeciwnym znakiem. W powyższym przykładzie kontrola została przeprowadzona (poprzez zaznaczenie par łańcuchów odpowiadającymi sobie kolorami) i zakończona pozytywnie.

Zadanie 2:

hierarchiczne rozwinięcie obrazu -podział zgodny z drzewem 4kowym - przebieg linii fraktalnej Peana.

Linia fraktalna Peana umożliwia budowę związków hierarchicznych (bloków pikseli), dalsze stopnie o identycznym kształcie, wykonuje krótkie przebiegi w lokalnej przestrzeni, oscyluje w lokalnej przestrzeni, minimalna liczba skoków, małe skoki, niezmiernie oszczędny zapis. Każdy kolejny powstaje z 4 poprzednich. Linię fraktalną rysujemy na zasadzie odwróconej litery „Z”. Linia fraktalna składa się z 3 stopni:

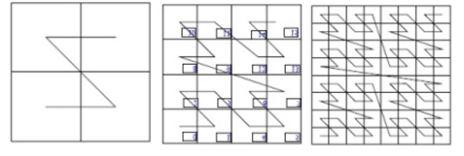
Drzewo czwórkowe:

Przykład drzewa czwórkowego: każde dziecko dostaje nazwisko ojca i swoje jedno, niepowtarzalne imię.

Zalety takiego podziału: -regularność, -łatwość zamiany na współrzędne, -obiekty o podobnych kodach zlokalizowane są po sąsiedzku, -kolejność narastania kodów w schemacie drzewa czwórkowego pokrywa się z kierunkiem przebiegania zgodnym z linią fraktalną Peana. Linia fraktalna jest konsekwencją podziału zgodnego z drzewem czwórkowym. Przy takim sposobie kodowania linia fraktalna ma 3 stopnie.

Drzewo czwórkowe jest zbiorem warstw tematycznych, ma strukturę listy.

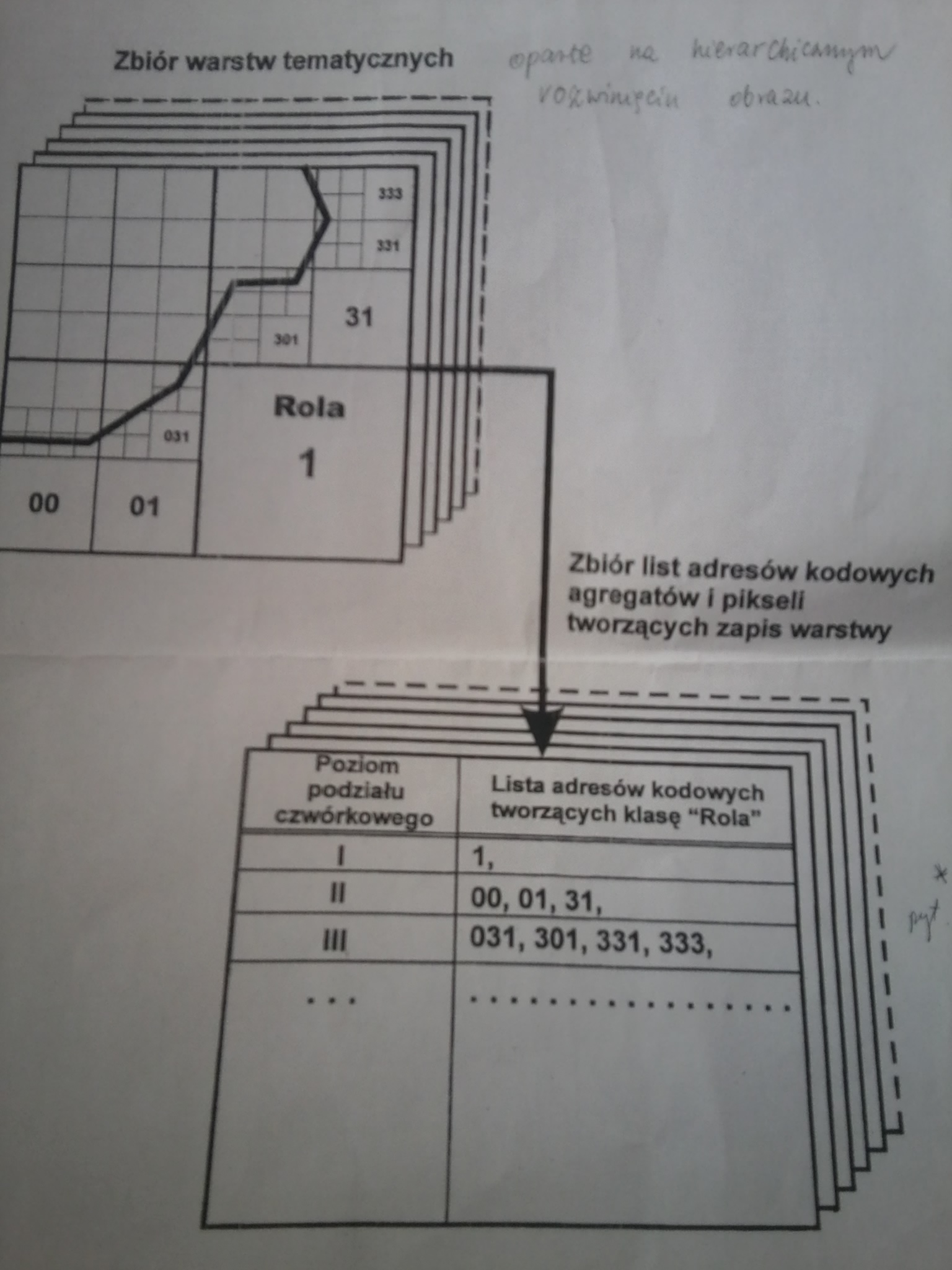
Opis przebiegu zapisu warstwy:

Poszukujemy pełnych agregatów, rejestrujemy kolejne maksymalne agregaty na poszczególnych poziomach podziału, które mieszczą się całkowicie w konturach obiektu danej klasy. Kody tych agregatów zapisujemy w postaci listy. Takie agregaty nie podlegają już dalszemu podziałowi, ponieważ posiadają ten sam atrybut. To daje znaczną oszczędność zapisu, ponieważ duże obszary są reprezentowane przez agregaty o maksymalnej wielkości. W miarę dopasowywania się granic obiektu, tworzymy zapis coraz mniejszych agregatów. Lista się powiększa ale i tak ten zapis jest o wiele bardziej oszczędny, niż zbiór globalny lub zbiór globalny w wersji rozwarstwionej.

Zadanie 3:

Nieregularna sieć trójkątów powstaje głownie jako efekt bezpośrednich pomiarów terenowych, gdzie cały zakres opracowania zapełnia się trójkątami opartymi o punkty pomiarowe. Ponieważ w tych modelach wykorzystywane są wszystkie punkty charakterystyczne model jest stosunkowo dokładny.

a) triangulacja Delaunay'a

Trójkąty tworzone są w ten sposób aby żaden z punktów nie należących do niego nie był

położony wewnątrz okręgu opisanego na trójkącie

b) Obszar Thiessena stanowi zbiór wszystkich punktów płaszczyzny, dla których odległość do punktu centralnego jest mniejsza od odległości do pozostałychpunktów. Ograniczenia tego obszaru stanowią odcinki symetralnych do boków triangulacji Delaunay'a.

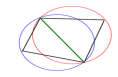
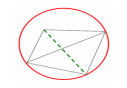
Triangulacja Delaunaya maksymalizuje wartość minimalnego kąta w trójkącie.( z spośród wszystkich wyselekcjonowanych punktów w kole do polaczenia pkt centralny zostanie polaczony z tymi punktami których symetralne utworzyły wielobok thiessen

Najczęściej stosowany jest algorytm Delaunay'a w którym wykorzystywane są poligony Thiessena. Triangulacja powinna być tak wykonana żeby: - tworzone trójkąty były możliwie zbliżone do równobocznych i możliwie małe; - każdy punkt ze zbioru punktów rozproszonych musi być uwzględniony; -procedura postępowania musi być jednoznaczną

Gdy nie są znane sposoby połączenia punktów stosuje sie triangulacje Delaunay'a z wykorzystaniem wieloboków Thiessena (mamy jak połączyć punkty rozproszone)

-trójkąty zbliżone do równobocznych

-każdy punkt musi być wykorzystany

-procedura musi być jednoznaczna

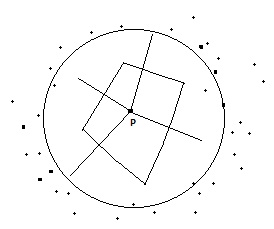
Przebieg tworzenia:

1. obieramy jakąś odległość R, równą lub większą niż średnia odl między pkt

2. zakreślamy okrąg o promieniu R na każdym punkcie, w tym okręgu znajda się punkty kandydujące do połączenia z tym punktem.

3. łączymy pkt P ze wszystkimi punktami kandydującymi i kreślimy symetralne tych odcinków

4. Z tych symetralnych budujemy najmniejszy wielobok. wielobok ten to wielobok Thiessena. Każdy punkt zawarty wewnątrz tego wieloboku jest bliżej punktu P niż innego punktu.

5. Spośród wszystkich pkt wyselekcjonowanych w okręgu punkt P będzie połączony tylko z tymi punktami, których symetralne utworzyły wielobok Thissena, te pkt będą tworzyły fragment przyszłej siatki.

6. Resztę punktów które nie utworzyły wieloboku się odrzuca.

7. Powyższa procedura powtarza się dalej dla wszystkich punktów rozproszonych

Matematycznie: budujemy ostrosłup i zakładamy, że V=0

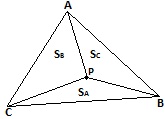
Wysokość punktu P jest średnią ważoną z wysokości trzech punktów, gdzie wagami są pola trójkątów leżących naprzeciwko.

Zadanie 4:

4.1). S=(R1 [A1] + R2 [A5]) x R3 [A8]

Komentarz: Najpierw musimy wykonać dwie projekcje: tabeli R1 zawierającej zbiór pracowników, tak aby pozostał jedynie atrybut z nazwiskiem pracownika (NAZWISKOPRAC), oraz tabeli R2 będącej zbiorem studentów, tak aby pozostał atrybut z nazwiskiem studenta (NAZWISKOSTUD). Projekcja jest to przekształcenie usuwające różnorodności, jest skreślaniem atrybutów i wybieraniem tylko tych, które nas interesują. Następnie przetworzone tablice po projekcji dodajemy do siebie. Dodawanie daje w wyniku relacje zawierające wszystkie krotki, a powtórzenia są usuwane. W dodawaniu wszystkie operanty muszą mieć takie same atrybuty, dlatego wykonano projekcję, aby obie dodawane tablice miały takie same atrybuty NAZWISKO. Nieważne tu jest, że nagłówki są różne (NAZWISKOPRAC i NAZWISKOSTUD), możemy wykonywać operacje na tych tablicach relacji, ponieważ mają atrybuty tego samego typu (nazwisko). Kolejnym krokiem było wykonanie projekcji tablicy relacji R3, tak aby pozostał tylko atrybut z nazwiskiem (NAZWISKOUZYT). Na koniec wykonano mnożenie pomiędzy wynikową tabelą z dodawania i wynikową tabelą po projekcji. Było to możliwe, ponieważ posiadały one takie same atrybuty. Wynikiem mnożenia jest obszar wspólny - krotki, które występują jednocześnie w obu relacjach. Jako wynik otrzymaliśmy nazwiska studentów i pracowników, którzy choć raz w tym semestrze wypożyczali sprzęt z instrumentarium.

4.2). S={(R1+R2) / R3} [NAZWISKO]

Komentarz: Logiczne jest, że będziemy te nazwiska poszukiwać na ogólnych listach nazwisk pracowników i studentów. Musimy więc stworzyć taką zsumowaną listę, a później wykreślić z niej te nazwiska, które występują w zbiorze R3, czyli wypożyczających sprzęt. Aby tego dokonać, najpierw wykonujemy dodawanie dwóch tablic relacji: R1i R2, a następnie od tablicy wynikowej odejmujemy listę korzystających z instrumentarium R3, aby dowiedzieć się kogo na tej liście nie było. Musimy w tym przypadku być bardzo ostrożni i nie wykonywać projekcji wcześniej, tylko na samym końcu, ponieważ gdy w działaniach na tablicach relacji występuje odejmowanie, to nie możemy robić wcześniej projekcji, bo to zlikwidowałoby różnorodność. Dlatego też ostatnim krokiem było wykonanie projekcji względem NAZWISKA (mimo iż nagłówki w każdej z tablic były różne NAZWISKOSTUD, -PRAC, -UZYT, to działania na tych tablicach były możliwe, ponieważ atrybuty były takie same). W wyniku otrzymaliśmy tabelę z nazwiskami studentów i pracowników, którzy w tym semestrze ani razu nie wypożyczyli sprzętu z instrumentarium.

---