Nr ćw. 310	Data 07.06.01	Jakacki Zbigniew	Wydział Elektryczny	Semestr II	Grupa E-3
mgr B. Jazurek				Przygotowanie	Wykonanie	Ocena

Temat: Wyznaczanie współczynnika załamania światła z pomiaru pozornej i rzeczywistej grubości płytek.

1. Część teoretyczna.

Światło, które po drodze do naszego oka przechodzi przez jedną lub więcej po­wierzchni załamujących, ma na ogól inny kierunek, niż gdyby biegło po linii pro­stej, w ośrodku jednorodnym. Z tego powodu obserwator odnosi wrażenie, że światło wychodzi z innego źródła niż to jest w rzeczywistości. Obserwowane źró­dło jest obrazem źródła rzeczywistego lub źródłem pozornym.

Spoglądając na przedmioty leżące na dnie naczynia z wodą wydaje nam się, że leżą one bliżej powierzchni niż w rzeczywistości. Przeciwnie, nurek spoglądający w górę na, powiedzmy, zwisającą gałąź drzewa będzie sądzić, że jest ona wyżej niż w rzeczywistości. W obu przypadkach mamy do czynienia z pozorną zmianą odległości wynikającą z załamania światła na granicy dwóch ośrodków.

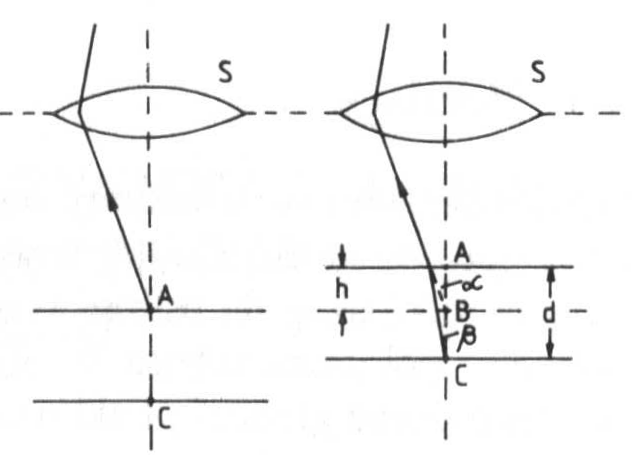
Przykład zjawiska, w którym występuje pozorna zmiana grubości, a także zasa­dę pomiaru tej grubości ilustruje poniższy rysunek. W lewej części rysunku widzimy soczewkę S (może nią być okular mi­kroskopu) ustawioną w ten sposób, że w ustalonym miejscu, niewidocznym na rysunku, powstaje ostry obraz punktu A znajdującego się na górnej powierzchni płytki.

Chcąc uzyskać ostry obraz punktu C znajdującego się na dolnej powierzchni płytki (prawa część rysunku), musimy całą płytkę przesunąć ku górze o odległość h. W tym położeniu promień wybiegający z punktu C „widziany jest" przez so­czewkę, jakoby wychodził z punktu B. W tym samym miejscu co poprzednio powstaje obraz pozornego źródła B. czyli rzeczywistego źródła C.

Według prawa załamania światła stosunek sinusów kąta padania α i kąta za­łamania β jest dla danej pary ośrodków wielkością stalą, równą stosunkowi bez­względnych współczynników załamania obu ośrodków.

Wartość bezwzględnego współczynnika załamania otrzymujemy z powyższego równania. Gdy jednym z ośrodków jest próżnia (n₁= l). Prawo załamania światła na granicy próżnia - ośrodek, a także w przybliżeniu na granicy powietrze - ośro­dek przyjmuje wtedy postać:

gdzie n oznacza bezwzględny współczynnik załamania dowolnego ośrodka.

W celu obliczenia pozornej grubości h zakładamy, że promienie biegnące w płytce tworzą bardzo mały kąt z prostopadłą padania. W tej sytuacji możemy zastąpić sinusy kątów samymi kątami

Wstawiając powyższe wartości do poprzedniego równania, otrzymujemy związek między grubością pozorną h i rzeczywistą d.

Grubość rzeczywistą mierzymy mikromierzem, grubość pozorną - za pomocą mikroskopu. Na górnej i dolnej powierzchni badanej płytki znajdują się rysy. Na­stawiamy mikroskop na ostrość widzenia rysy górnej, a następnie dolnej. Jeżeli oznaczymy położenia tubusa w obu przypadkach odpowiednio przez a_g i a_d wówczas pozorna grubość płytki wynosi h = a_d - a_g.

2. Przebieg ćwiczenia.

Na początku ćwiczenia należy pomierzyć grubości rzeczywiste za pomocą mikrometru. Następnie należy przystąpić do mierzenia grubości pozornej za pomocą mikroskopu, ustawiając mierzoną płytkę na stoliku mikroskopu, poczym znaleźć położenie a_d, przy którym wyraźnie widać dolną rysę na płytce, a następnie położenie a_g, przy którym powstaje wyraźny obraz rysy górnej. Powtarzać tą czynność kilka razy dla upewnienia się prawidłowości pomiaru.

3. Pomiary i obliczenia.

Grubości rzeczywiste badanych płytek wynoszą odpowiednio:

d₁ = 1,46 ± 0,01 mm

d₂ = 2,45 ± 0,01 mm

d₃ = 4,10 ± 0,01 mm

d₄ = 4,15 ± 0,01 mm

Natomiast grubości pozorne wynoszą odpowiednio:

Lp.	Płytka 1			Płytka 2			Płytka 3			Płytka 4
		ag	ad	h3	ag	ad	h3	ag	ad	h3	ag	ad	h4
1	3,4	4,25	0,85	0,6	3,18	2,58	0,63	4,72	4,09	0,6	4,77	4,17
2	4,4	5,52	1,12	0,75	3,26	2,51	1,02	4,97	3,95	0,65	4,9	4,25
3	4,46	5,51	1,05	0,56	3,14	2,58	0,93	4,97	4,04	0,73	4,92	4,19
4	3,3	4,73	1,43	0,81	3,34	2,53	1	5	4	0,6	4,78	4,18
5	3,34	4,39	1,05	0,66	3,15	2,49	1,03	5,03	4	0,34	4,5	4,16
Średnia h1			1,1	Średnia h1		2,538	Średnia h1		4,016	Średnia h1		4,19
Odch. Stan. σh1			0,210238	Odch. Stan. σh1		0,040866	Odch. Stan. σh1		0,052249	Odch. Stan. σh1		0,035355
h1=1,1±0,21				h2 =2,53±0,04			h2 =4,016±0,052			h2 =4,19±0,035

Obliczam współczynnik załamania oraz błąd przy pomocy różniczki logarytmicznej:

δ


n₁ = 0,242

δ


n₂ = 0,124

δn₃ = 0,156

δn₄ = 0,123

Czyli ostateczne wyniki wynoszą:

n₁ = 1,318 ± 0,242

n₂ = 0,965 ± 0,124

n₃ = 1,02 ± 0,156

n₄ = 0,990 ± 0,123

4. 
   Wnioski.

Otrzymane wyniki podczas ćwiczenia nie są zgodne z tablicowymi. Choć wykonanie jego odbyło się prawidłowo. Znaczna odchyłka mogła być spowodowana znacznymi luzami w mikroskopie a także mikrometrem służącym do pomiaru górnej i dolnej kreski. Powstanie błędu paralaksy mogło wpłynąć także na zniekształcenia ostatecznego wyniku.

---