Nr ćwicz. 310	Data		Wydział	Semestr	Grupa
Prowadzący:			Przygotowanie	Wykonanie	Ocena

Pomiar grubości płytek mikroskopem

1. Wstęp teoretyczny

Światło wpadające do oka ludzkiego, w wyniku załamania na granicy różnych ośrodków, ma na ogół inny kierunek, niż gdyby biegło po linii prostej w jednorodnym ośrodku. Widzimy zatem nie źródło rzeczywiste, ale jedynie jego obraz, zwany również źródłem pozornym. Typowym przykładem może być złudzenie, któremu ulegamy patrząc na dno jeziora przez czystą wodę. Wydaje się ono być na wyciągnięcie ręki, podczas gdy w rzeczywistości woda ma w danym miejscu nawet do kilku metrów głębokości. Jest to empiryczny dowód na pozorną zmianę odległości, wynikającą z załamania światła na granicy dwóch ośrodków - wody i powietrza.

Podobne zjawisko można zaobserwować, jeśli rozważymy przezroczystą płytkę i będziemy obserwować jej górną i dolną płaszczyznę. Przesunięcie płytki od położenia, w którym wyraźnie widać górną krawędź do położenia, w którym uzyskamy ostry obraz dolnej krawędzi, nie jest wcale grubością płytki.

Wykorzystując prawo Snella, mówiące o zależnościach pomiędzy kątami padania światła w dwóch ośrodkach a ich współczynnikami załamania:

,

w przypadku, gdy jednym z ośrodków jest powietrze (dla którego można przyjąć z dużym przybliżeniem n=1) a drugim płytka, w której kąty pomiędzy promieniami, a prostopadłą padania są małe (czyli sinα ≈ α), możemy obliczyć pozorną grubość płytki. Po podstawieniu kątów załamania światła źródła pozornego i rzeczywistego oraz n=1 dla powietrza, otrzymujemy z prawa Snella wartość bezwzględnego współczynnika załamania światła ze wzoru:

2. Opis ćwiczenia

Ćwiczenie przeprowadzałem dwuetapowo, badając 6 płytek, na początku oznaczając je odpowiednio numerami. Pierwszym krokiem było zmierzenie za pomocą mikromierza ich rzeczywistej grubości. Te pomiary wykonywałem trzykrotnie. Drugim etapem było badanie pozornej grubości płytek za pomocą mikroskopu, mierząc przesunięcie stolika od punktu, w którym widoczna była jedna płaszczyzna płytki do punktu, w którym widziałem drugą jej płaszczyznę. Tutaj wykonałem po 6 pomiarów dla każdej z badanych płytek, badając kolejno grubość pozorną każdej z nich, po każdym pomiarze „psując” ostrość obrazu w okularze mikroskopu.

3. 
   Schemat ćwiczenia

1. Pomiar rzeczywistej grubości płytek

2. 
   Pomiar pozornej grubości płytek

4. Dane eksperymentalne

1. Pomiar rzeczywistej grubości płytek (w mm) mikromierzem

	numer płytki
Pomiar	1	2	3	4	5	6
1.	1,46	3,75	4,14	5,86	4,03	1,46
2.	1,46	3,76	4,14	5,86	4,03	1,45
3.	1,46	3,76	4,13	5,86	4,03	1,46

2. Pomiar pozornej grubości płytek - wskazy pozycji wyjściowej (w_w) i końcowej (w_k) przyrządu mierniczego.

nr pomiaru
nr płytki	ww	wk	ww	wk	ww	wk	ww	wk	ww	wk	ww	wk
1.	3,86	4,58	3,65	4,45	3,62	4,60	3,41	4,56	3,61	4,62	3,50	4,51
2.	1,21	3,60	1,35	3,89	1,40	3,80	1,36	3,79	1,31	3,85	1,37	3,89
3.	0,94	3,33	0,92	3,37	0,91	3,30	0,96	3,32	0,98	3,40	0,95	3,37
4.	0,23	3,25	0,24	3,05	0,24	3,06	0,23	3,03	0,25	2,95	0,24	3,12
5.	1,15	3,83	1,19	3,83	1,08	3,78	0,95	3,90	0,94	3,83	1,13	3,79
6.	3,57	4,45	3,84	4,65	3,60	4,50	3,58	4,44	3,57	4,63	3,49	4,64

5. Dyskusja błędów

1. Błędy systematyczne

Błędy systematyczne mikromierza i przesuwu stolika mikroskopu wynosiły ± 0,005 mm.

2. Błędy przypadkowe

Błędy pojawiające się w początkowych etapach ćwiczenia wynikały z nieznajomości praktycznej techniki pomiarowej, dodatkowo później odczuwalne było zmęczenie wzroku i więcej czasu wymagało ustawienie mikroskopu tak, aby ostro widoczna była odpowiednia płaszczyzna płytki. Gdybym dysponował większą ilością czasu przeprowadziłbym pojedyncze pomiary dla wszystkich płytek od 1 do 6, za każdym razem zmieniając badaną płytkę. W ten sposób również wykonałbym 6 pomiarów, ale każda z płytek byłaby badana wraz z pozostałymi w odpowiednich chwilach trwania ćwiczenia, co umożliwiłoby zobiektywizowanie czynników mogących fałszować wyniki, jakimi były właśnie nieznajomość techniki pomiarowej i zmęczenie wzroku.

Drugim źródłem błędów była ograniczona dokładność przyrządów pomiarowych, zwłaszcza mikroskopu, którego stolik bardzo trudno się przesuwał i w związku z tym czasem niemożliwe było ustawienie najlepszej ostrości.

3. Obliczenie średnich grubości rzeczywistych d płytek

nr płytki	grubość rzeczywista średnia di [mm]	błąd średniej (odchylenie standardowe x współczynnik Studenta-Fishera)
1.	d1 = 1,460	0 x 1,3 = 0
2.	d2 = 3,757	0,006 x 1,3 = 0,008
3.	d3 = 4,137	0,006 x 1,3 = 0,008
4.	d4 = 5,860	0 x 1,3 = 0
5.	d5 = 4,030	0 x 1,3 = 0
6.	d6 = 1,457	0,006 x 1,3 = 0,008

Obliczone rzeczywiste grubości średnie są obciążone błędem mniejszym od najmniejszej podziałki mikromierza (0,01 mm), ale większy od jej połowy. Ta niedokładność pomiaru wynikała z dużej dokładności przyrządu i mimo wszystko subiektywności pomiaru (kwestia dociśnięcia śruby mikromierza i grubości konkretnego badanego miejsca na płytce).

4. Obliczenie średnich grubości pozornych h płytek

h_i = w_ki - w_wi

płytka	grubość pozorna hj (gdzie j jest numerem pomiaru) [mm]						hi średnia	błąd średniej^*
1.	h1 = 0,72	h2 = 0,80	h3 = 0,98	h4 = 1,15	h5 = 1,01	h6 = 1,01	h1=0,945	0,192
2.	h1 = 2,39	h2 = 2,54	h3 = 2,40	h4 = 2,43	h5 = 2,54	h6 = 2,52	h2=2,470	0,084
3.	h1 = 2,39	h2 = 2,45	h3 = 2,39	h4 = 2,36	h5 = 2,42	h6 = 2,42	h3=2,405	0,037
4.	h1 = 3,02	h2 = 2,81	h3 = 2,82	h4 = 2,80	h5 = 2,70	h6 = 2,88	h4=2,838	0,128
5.	h1 = 2,68	h2 = 2,64	h3 = 2,70	h4 = 2,95	h5 = 2,89	h6 = 2,66	h5=2,753	0,158
6.	h1 = 0,88	h2 = 0,81	h3 = 0,90	h4 = 0,86	h5 = 1,06	h6 = 1,15	h6=0,943	0,158

^* - odchylenie standardowe x współczynnik Studenta-Fishera dla 6 pomiarów ( = 1,2).

Największym błędem charakteryzuje się pierwszy pomiar, co wynika z omówionej już niedoskonałości techniki pomiarowej. Po trzecim pomiarze następuje zmniejszenie dokładności, spowodowane zmęczeniem wzroku, którego nie zniwelowała wprawa nabyta w trakcie ćwiczenia.

6. Zestawienie wyników

Współczynniki załamania światła n_i dla poszczególnych płytek:




n₁ = 1,545 ± 0,192 n₂ = 1,521 ± 0,092 n₃ = 1,720 ± 0,045

n₄ = 2,065 ± 0,128 n₅ = 1,464 ± 0,158 n₆ = 1,545 ± 0,166

7. Wnioski końcowe

Wziąwszy pod uwagę błędy obliczonych bezwzględnych współczynników załamania światła można wysnuć wniosek, iż rosną one wraz ze wzrostem grubości płytki. Po zestawieniu obliczeń z wynikami poprzedniego ćwiczenia (dotyczącego współczynników załamania światła dla cieczy) można stwierdzić, że współczynnik załamania światła rośnie wraz ze wzrostem gęstości ośrodka. Dla danych uzyskanych w toku ćwiczenia obrazuje to wykres zamieszczony poniżej.


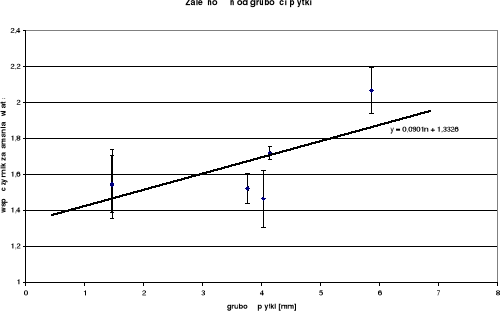
Rozważając wyniki wszystkich etapów pomiarów płytek 1 i 6 oraz 3 i 4 można również zauważyć, że obliczenie współczynnika załamania przez pomiar względnej grubości płytek jest mniej dokładne przy cienkich obiektach. Wynika to ze stosunku błędu pomiaru do grubości samej płytki.

laboratorium optyczne sprawozdanie z ćw. nr 310 strona nr 1




---