Nr ćwicz. 302	Data		Wydział	Semestr	Grupa
Prowadzący:			Przygotowanie	Wykonanie	Ocena

Badanie siatki dyfrakcyjnej

1. Wstęp teoretyczny

Światło jest falą elektromagnetyczną, tzn. rozchodzącą się w przestrzenie zmianą pół elektrycznego i magnetycznego. Dla zjawisk optycznych decydującą rolę odgrywa wektor natężenia pola elektrycznego E - wektor elektryczny. Do przedstawienia fali świetlnej wystarczy zatem określenie wektora E w funkcji czasu i współrzędnych przestrzennych. Przyjmując, że fala o okresie T, długości fali λ i fazie początkowej ϕ₀ biegnie w kierunku osi X układu, możemy zapisać funkcję falową w postaci:

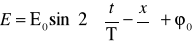
Każda fala może podlegać dyfrakcji - ugięciu (np. przy przechodzeniu przez szczelinę) i interferencji - nałożeniu się na inne fale. Wynika to z zasady Huygensa, w myśl której każdy punkt w przestrzeni, do którego dochodzi fala, staje się źródłem nowej fali kulistej.

Aby można zaobserwować interferencję, potrzeba nie tylko więcej niż jednej fali - fale te dodatkowo muszą być koherentne, czyli mieć stałą (niezmienną w czasie) różnicę faz
Δϕ = ϕ₁ - ϕ₀. Jednak jeśli fale te wychodzą z dwóch różnych źródeł w przestrzeni, nałożenie się fal spowoduje w jednych miejscach wzmocnienie, a w innych osłabienie fali wynikowej. Maksima powstaną w miejscach, gdzie Δϕ = 2kπ a różnica dróg ΔS = kλ, minima natomiast przy Δϕ = (2k+1)π i ΔS = (k+0,5)λ dla k = 0, 1, 2, …

Jeśli światło spotka na swojej drodze siatkę dyfrakcyjną, czyli większą szczelin o tej samej szerokości, równoległych do siebie i równo odległych, których wielkość będzie zbliżona do długości fali, to obraz otrzymany po przejściu przez nie będzie wynikiem dyfrakcji na każdej ze szczelin i interferencji wszystkich nowopowstałych, zgodnie z zasadą Huygensa, fal. Maksima interferencyjne wystąpią zgodnie z podanymi powyżej warunkami, czyli dla przebytej drogi równej wielokrotności fali. Centralne maksimum wystąpi zatem dla zerowego kąta padania ϑ₀ oraz dla kątów, które spełniają związek:

dsinϑ = mλ,

gdzie d jest odległością między środkami sąsiednich szczelin, zwaną stałą siatki dyfrakcyjnej, a m = 1, 2, 3, …

Powyższy wzór, po przekształceniu do postaci:

może służyć do wyznaczenia stałej siatki dyfrakcyjnej, pod warunkiem, że zastosujemy światło o określonej długości fali i spektrometr, umożliwiający dokładny pomiar wartości kątów ϑ dla poszczególnych maksimów.

2. Opis ćwiczenia

Ćwiczenie przeprowadzałem dla dwóch siatek dyfrakcyjnych: A i B. Dla obu siatek wykonałem po 3 pomiary, badając najpierw położenie prążka zerowego rzędu a potem kolejno maksima 1, 2 i 3 rzędu lewostronne i później prawostronne siatki A i siatki B.

3. Schemat ćwiczenia

1. Schemat jednej serii pomiarów prążków interferencyjnych

2. Obliczenie kątów ugięcia ϑ dla każdego rzędu prążków w każdym pomiarze.

3. Obliczenie stałej siatki dla każdego pomiaru.

4. Obliczenie wartości średniej stałej siatki dyfrakcyjnej.

4. Dane eksperymentalne

1. Kąty odpowiadające położeniu prążka zerowego dla poszczególnych pomiarów

	siatka
Pomiar	A		B
1.	153^o07,0'		153^o07,0'
2.	153^o11,0'		153^o11,0'
3.	153^o08,0'		153^o10,0'

2. Siatka A

	numer rzędu i strona
Pomiar	1l	2l	3l	1p	2p	3p
1.	146^o37,5'	139^o37,5'	132^o37,0'	160^o02,0'	167^o06,0'	174^o31,0'
2.	146^o22,5'	139^o30,0'	132^o19,5'	160^o00,0'	166^o49,0'	174^o00,0'
3.	146^o22,5'	139^o30,0'	132^o30,0'	160^o00,0'	166^o55,0'	174^o12,0'

3. Siatka B

	numer rzędu i strona
Pomiar	1l	2l	3l	1p	2p	3p
1.	146^o22,5'	139^o30,0'	132^o21,5'	160^o00,0'	166^o51,5'	173^o52,0'
2.	146^o22,5'	139^o34,5'	132^o30,0'	160^o00,0'	166^o52,5'	174^o04,0'
3.	146^o22,5'	139^o34,5'	132^o30,0'	160^o00,0'	166^o55,0'	174^o09,5'

5. Obliczenie wyników i dyskusja błędów

1. Błędy systematyczne

Każdy pomiar spektroskopem był obarczony błędem wynikającym z dokładności urządzenia,
tj. ±0,5'

2. Obliczenie kątów ugięcia dla każdego rzędu i pomiaru

1. Siatka A

	wartości bezwzględne kątów ugięcia
Pomiar	1l	2l	3l	1p	2p	3p
1.	6^o29,5'	13^o29,5'	20^o30,0'	6^o55,0'	13^o59,0'	21^o24,0'
2.	6^o48,5'	13^o41,0'	20^o51,5'	6^o49,0'	13^o38,0'	20^o49,0'
3.	6^o45,5'	13^o38,0'	20^o38,0'	6^o52,0'	13^o47,0'	21^o04,0'

2. Siatka B

	wartości bezwzględne kątów ugięcia
Pomiar	1l	2l	3l	1p	2p	3p
1.	6^o44,5'	13^o37,0'	20^o45,5'	6^o53,0'	13^o44,5'	20^o45,0'
2.	6^o48,5'	13^o36,5'	20^o41,0'	6^o49,0'	13^o41,5'	20^o53,0'
3.	6^o47,5'	13^o35,5'	20^o40,0'	6^o50,0'	13^o45,0'	20^o59,5'

Każda z wartości bezwzględnych kątów ugięcia jest obarczona błędem wynikającym ze sposobu liczenia kąta ugięcia: ϑ = |ϑ₀ - ϑ_i|, gdzie i jest rzędem maksimum. Po obliczeniu różniczki zupełnej otrzymujemy błąd Δϑ = ± 1'

3. Obliczenie stałej siatki z każdego pomiaru (dla λ = 589,6 nm; wyniki w μm)




Rachunek jednostek:


Obliczenie błędu (metodą różniczki logarytmicznej):







1. Siatka A




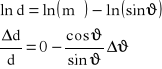
Rząd 1 z 1 pomiaru:

strona	stała siatki [μm]	błąd [μm]
lewa	5,215	± 0,764
prawa	4,896	± 0,673

Rząd 1 z 2 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	4,974	± 0,694
prawa	4,967	± 0,693

Rząd 1 z 3 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	5,010	± 0,705
prawa	4,932	± 0,683

Rząd 2 z 1 pomiaru:

strona	stała siatki [μm]	błąd [μm]
lewa	5,054	± 0,351
prawa	4,880	± 0,327

Rząd 2 z 2 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	4,985	± 0,341
prawa	5,003	± 0,344

Rząd 2 z 3 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	5,003	± 0,344
prawa	4,949	± 0,336

Rząd 3 z 1 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	5,051	± 0,225
prawa	5,074	± 0,222

Rząd 3 z 2 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	4,968	± 0,217
prawa	4,977	± 0,218

Rząd 3 z 3 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	5,020	± 0,222
prawa	4,921	± 0,213




2. Siatka B




Rząd 1 z 1 pomiaru:

strona	stała siatki [μm]	błąd [μm]
lewa	5,023	± 0,708
prawa	4,920	± 0,679

Rząd 1 z 2 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	4,975	± 0,695
prawa	4,968	± 0,693

Rząd 1 z 3 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	4,986	± 0,698
prawa	4,955	± 0,689

Rząd 2 z 1 pomiaru:

strona	stała siatki [μm]	błąd [μm]
lewa	5,009	± 0,345
prawa	4,964	± 0,338

Rząd 2 z 2 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	5,012	± 0,345
prawa	4,982	± 0,341

Rząd 2 z 3 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	5,018	± 0,346
prawa	4,961	± 0,338

Rząd 3 z 1 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	4,991	± 0,220
prawa	4,993	± 0,220

Rząd 3 z 2 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	5,008	± 0,221
prawa	4,962	± 0,217

Rząd 3 z 3 pomiaru

strona	stała siatki [μm]	błąd [μm]
lewa	5,012	± 0,222
prawa	4,938	± 0,215




4. Obliczenie średniej stałej siatki dyfrakcyjnej i błędu średniej

Ponieważ średnia jest liczona z 18 wyników dla każdej z siatek, współczynnik
Studenta-Fishera = 1. Porównanie średniej z wartościami błędów uzyskanymi za pomocą metody różniczki logarytmicznej wskazuje na poprawność rozumowania (obliczona za pomocą średniej stała siatki mieści się w granicach błędów pojedynczych pomiarów).

1. Siatka A

d_A = 4,993 [μm]

błąd średniej =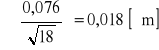


2. Siatka B

d_B = 4,982 [μm]

błąd średniej =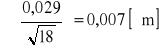


6. Zestawienie wyników

Na podstawie błędów obliczonych ze średniej otrzymujemy:

d_A = 4,993 ± 0,4% (0,018) [μm]

d_B = 4,982 ± 0,1% (0,007) [μm]

Można zatem uznać, że badane siatki miały stałe d różniące się o 10 [nm] (0,01 [μm])

7. Wnioski końcowe

Za szczególnie zadowalające można uznać wyniki błędów statystycznych obliczeń, mieszczące się w granicach 4 ‰.

Wziąwszy pod uwagę błędy pojedynczych pomiarów wyznaczone metodą różniczki logarytmicznej można stwierdzić, że błąd pomiaru maleje wraz ze wzrostem rzędu badanych maksimów, można by zatem pominąć pomiary maksimów pierwszego rzędu bez nadmiernego wpływu na dokładność wyznaczenia stałej siatki dyfrakcyjnej.

Dla siatki B uwzględniając jedynie wyniki pomiarów maksimów 2 i 3 rzędu otrzymujemy
d_B = 4,988 ± 0,16% (0,008) [μm], czyli wzrost błędu statystycznego o 0,6 ‰ (dla 12 pomiarów współczynniki Studenta-Fishera nadal wynoszą 1).

laboratorium optyczne sprawozdanie z ćw. nr 308 strona nr 1

Wojciech Kasprzak I rok ET grupa E-4

laboratorium optyczne sprawozdanie z ćw. nr 308 strona nr 7

---