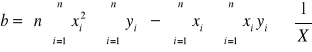I Logistyka	Katarzyna Szewczyk	Data wykonania ćwiczenia: 26.02.2009
	Temat: Pomiar długości fali świetlnej na podstawie interferencji w układzie optycznym do otrzymywania pierścieni Newtona

1. Wprowadzenie

1. opis teoretyczny:

Rozdzielenie wiązki światła na dwie wiązki zawierające po jednej części każdego ciągu falowego uzyskuje się m.in. w układzie do otrzymania pierścieni Newtona. Obraz interferencyjny w postaci prążków w kształcie współśrodkowych okręgów uzyskuje się tu przez umieszczenie soczewki płasko-wypukłej o dużym promieniu krzywizny na płaskiej płytce szklanej, pomiędzy którymi istnieje cienka warstwa powietrza o stopniowo rosnącej grubości w miarę oddalania się od punktu centralnego (styczności). Monochromatyczne promienie równoległe, padające prostopadle na płaską powierzchnię soczewki przechodzą przez szkło i częściowo ulegają odbiciu od powietrza (na drugiej powierzchni granicznej soczewki), a częściowo przechodzą dalej przez warstwę powietrza, ulegają odbiciu od płytki szklanej i wracają do obserwatora. Część wiązki odbita i ta, która dwukrotnie przeszła przez warstwę powietrza o grubości d odbijając się interferują ze sobą. Różnica ich dróg optycznych wynosi:

Wielkość
wynika ze zmiany fazy na przeciwną przy odbiciu od ośrodka optycznie gęstszego na powierzchni płytki.

Rys. 1 Geometryczna interpretacja warunku interferencji.

W celu ustalenia zależności między promieniami pierścieni jasnych lub ciemnych i długością fali przeprowadzamy analizę geometryczną:

Ponieważ d jest bardzo małe w porównaniu z 2R, można ostatnią zależność wyrazić:

skąd

Gdy różnica dróg optycznych równa się nieparzystej wielokrotności połówek długości fali, powstaje pierścień ciemny o promieniu r_n:

Podstawiając kolejno za n 1,2,3, . . ., a następnie odejmując stronami dowolną parę równań otrzymujemy:

gdzie: r_m - promień pierścienia kolejnego,

r_n - promień pierścienia wcześniejszego,

R - promień krzywizny soczewki,

m, n - rzędy pierścieni ciemnych.

1. przebieg ćwiczenia:

W ćwiczeniu należy dokonać pomiaru jest długości fali światła monochromatycznego, które uzyskuje się przez wydzielenie z wiązki światła białego, wąskiego przedziału długości fal przy użyciu filtrów interferencyjnych.

Ćwiczenie dzieli się na dwie części:

• Wyznaczenie promienia krzywizny soczewki:

Promienie kolejnych pierścieni należy mierzyć w dwie strony od środka w celu uśrednienia wartości. Promień ten wyznaczamy przy oświetleniu monochromatyczną wiązką światła o znanej długości fali, otrzymaną z palnika sodowego przystawionego do oświetlacza. Po ustawieniu ostrości mikroskopu, naprowadzić punkt centralny pierścieni tak, aby pokrywał się z przecięciem krzyża na okularze mikroskopu. Promienie krzywizny soczewki wyliczmy przekształcając wzór na λ :

gdzie r_m i r_n - wartości średnie promieni niezbyt odległych od siebie

λ_Na - długość fali równa 589^. 10 ^-9 m.

• Wyznaczanie długości fali światła monochromatycznego otrzymanego przy użyciu filtrów interferencyjnych:

W tej części ćwiczenia należy użyć lampki mikroskopowej z żarowym źródłem światła, a następnie między nią a oświetlaczem umieścić filtr interferencyjny. Pomiar promieni przeprowadzamy w sposób podobny jak w pierwszej części ćwiczenia. Następnie obliczamy długość fali.

Pomiary i obliczenia umieszczone zostały w poniższej tabeli.

Rodzaj światła	Rząd pierścieni ciemnych n	Odczyt z mikrometru		Średnia wartość pierścienia	Promień krzywizny soczewki	Długość fali
							W przód	W tył
	Sodowe	1	0,53	0,52	0,53		477	589
		5	1,32	1,29	1,31		609
		10	1,77	1,64	1,71		410
		15	2,14	2,09	2,12		533
		20	2,43	2,40	2,42		462
		25	2,70	2,61	2,66		414
		30	2,94	2,85	2,90		453
	Filtr 1 (czerwone)	1	0,48	0,45	0,47		480
		4	1,22	1,12	1,17
		8	1,64	1,53	1,59
		12	1,97	1,86	1,92
		16	2,24	2,15	2,20
		20	2,50	2,40	2,45
	Filtr 2 (pomarań-czowe)	1	0,52	0,45	0,49			480
		4	1,18	1,08	1,13
		8	1,56	1,46	1,51
		12	1,86	1,77	1,82
		16	2,13	2,03	2,08
		20	2,35	2,26	2,31
	Filtr 3 (zielone)	1	0,56	0,47	0,52			480
		4	1,23	1,09	1,16
		8	1,57	1,47	1,52
		12	1,87	1,85	1,86
		16	2,12	2,00	2,06
		20	2,34	2,29	2,32
	Filtr 4 (niebieskie)	1	0,56	0,46	0,51			480
		4	1,18	1,05	1,12
		8	1,53	1,40	1,47
		12	1,78	1,81	1,80
		16	1,99	2,01	2,00
		20	2,13	2,23	2,18

Niepewności pomiarów promienia r:

• niepewność wzorcowania: Δ_dr = 0,01 mm

• niepewność eksperymentatora: Δ_er = 0,1 mm

2. Obliczenia

Promień krzywizny R soczewki wyliczam z przekształcenia zależności
, tj.
. Zatem podstawiając kolejne zmierzone dane do wzoru otrzymam:

,

,

wyniki pozostałych obliczeń promienia krzywizny soczewki zamieszczone są w tabeli powyżej.

Średni promień krzywizny wynosi zatem: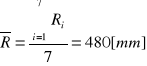

Niepewność standardową u(r_n) wyznaczam metodą typu B:

.

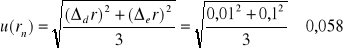
Niepewność złożoną
wyliczam z prawa przenoszenia niepewności:

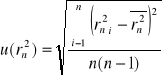
, zatem

i
1	0,53	0,28	-4,11	16,92
2	1,31	1,72	-2,68	7,17
3	1,71	2,92	-1,47	2,16
4	2,12	4,49	0,10	0,01
5	2,42	5,86	1,46	2,14
6	2,66	7,08	2,68	7,19
7	2,90	8,41	4,02	16,13

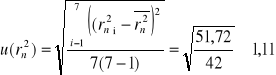
Metodą regresji liniowej wyznaczam współczynnik kierunkowy a prostej f(n) = r_n²:

-->
[Author:K.S]

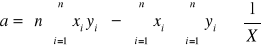
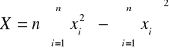
Podstawiając wielkości do wzorów otrzymam:

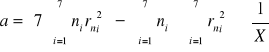
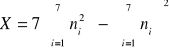
i	ni	ni^2
1	1	1	0,28	0,2809
2	5	25	1,72	8,5805
3	10	100	2,92	29,241
4	15	225	4,49	67,416
5	20	400	5,86	117,128
6	25	625	7,08	176,89
7	30	900	8,41	252,3
	Σ = 106	Σ = 2276	Σ = 30,76	Σ = 651,84

stąd współczynnik kierunkowy a = 0,28.

Dla wyliczenia niepewności standardowej korzystam ze wzorów:

, gdzie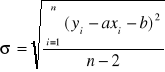
,

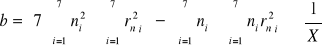
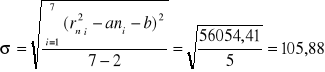
	ni	ani
0,28	1	0,28	8035,17
1,72	5	1,4	7978,76
2,92	10	2,8	8013,10
4,49	15	4,2	7982,64
5,86	20	5,6	7989,43
7,08	25	7	8021,78
8,41	30	8,4	8033,54
			Σ = 56054,41

Z zależności
obliczam promień krzywizny soczewki:
mm oraz niepewność standardową u(R):

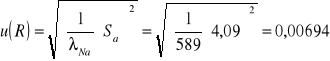
Wyznaczanie długości fali światła monochromatycznego otrzymanego przy użyciu filtrów interferencyjnych

Długość fali

1. filtr I (światło czerwone)

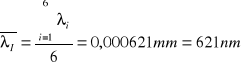
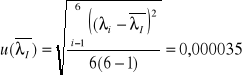
3. filtr II (światło pomarańczowe)

λ₁ = 0,000500

λ₂ = 0,000665

λ₃ = 0,000594

λ₄ = 0,000575

λ₅ = 0,000563

λ₆ = 0,000556

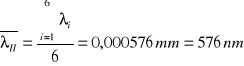
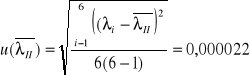
4. filtr III (światło zielone)

λ₁ = 0,000563

λ₂ = 0,000701

λ₃ = 0,000602

λ₄ = 0,000601

λ₅ = 0,000553

λ₆ = 0,000561

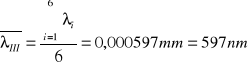
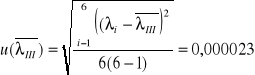
5. filtr IV (światło niebieskie)

λ₁ = 0,000542

λ₂ = 0,000653

λ₃ = 0,000563

λ₄ = 0,000563

λ₅ = 0,000521

λ₆ = 0,000495

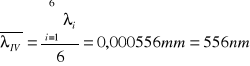
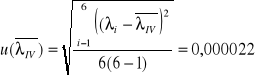
Współczynnik kierunkowy a oraz niepewność standardowa dla:

• filtra I

i	ni	ni^2	rn^2i	ni rn^2i
1	1	1	0,22	0,22
2	4	16	1,37	5,48
3	8	64	2,53	20,22
4	12	144	3,69	44,24
5	16	256	4,84	77,44
6	20	400	6,00	120,05
		Σ = 881	Σ = 18,65	Σ = 267,65

X = 1565

a = 0,30

b = 52,55

σ = 64,29

S_a = 3,98

• filtra II

i	ni	ni^2	rn^2i	ni rn^2i
1	1	1	0,24	0,24
2	4	16	1,28	5,11
3	8	64	2,28	18,24
4	12	144	3,31	39,75
5	16	256	4,33	69,22
6	20	400	5,34	106,72
		Σ = 881	Σ = 16,77	Σ = 239,28

X = 1565

a = 0,26

b = 47,32

σ = 57,77

S_a = 3,58

• filtra III

i	ni	ni^2	rn^2i	ni rn^2i
1	1	1	0,27	0,27
2	4	16	1,35	5,38
3	8	64	2,31	18,48
4	12	144	3,46	41,52
5	16	256	4,24	67,90
6	20	400	5,38	107,65
		Σ = 881	Σ = 17,01	Σ = 241,20

X = 1565

a = 0,26

b = 48,06

σ = 58,63

S_a = 3,63

• filtra IV

i	ni	ni^2	rn^2i	ni rn^2i
1	1	1	0,26	0,26
2	4	16	1,25	5,02
3	8	64	2,16	17,29
4	12	144	3,24	38,88
5	16	256	4,00	64,00
6	20	400	4,75	95,05
		Σ = 881	Σ = 15,67	Σ = 220,49

X = 1565

a = 0,23

b = 44,33

σ = 53,95

S_a = 3,34

WNIOSKI:

W ćwiczeniu oprócz wyznaczenia długości fali dla poszczególnych filtrów należało także wyznaczyć promień krzywizny soczewki oraz współczynnik kierunkowy „a” prostej. Współczynnik należało wyznaczyć metodą regresji liniowej.

Długości fal światła monochromatycznego:

- filtr nr 1 : λ_Śr = 621 nm (± 35 )

- filtr nr 2 : λ_Śr = 575 nm (± 22 )

- filtr nr 3 : λ_Śr = 597 nm (± 23)

- filtr nr 4 : λ_Śr = 556 nm (± 22)

Uzyskana wartość współczynnika jest równa:

• dla lampy sodowej a = 0,28

• dla filtra 1 a = 0,30

• dla filtra 2 a = 0,26

• dla filtra 3 a = 0,26

• dla filtra 4 a = 0,23

Doświadczenie to trzeba prowadzić bardzo starannie, ponieważ polegało na bardzo dużej dokładności i precyzji. Najmniejsze nawet szturchnięcie mogło spowodować różnice w odczycie pierścieni.

Na błędy pomiarów miały wpływ między innymi takie czynniki jak :

- niedokładny odczyt z mikrometra,

- błędne ustawienia mikroskopu,

- niemożność dokładnego określenia środka pierścieni,

- duża trudność w odróżnieniu pierścieni o rzędzie n > 15,

- duża czułość układu na wpływ czynników zewnętrznych.

W tym wzorze podobno ma nie być tego n w pierwszym nawiasie… Ale nie sprawdzałam tego w necie i innych książkach - po prostu zrobiłam tak jak było w skrypcie







---