1/IV Cząstka wykonuje drgania harmoniczne. W odległości x1 i x2 od położenia równowagi jej prędkości wynoszą v1 i v2 (x2>x1 i v1>v2). Znaleźć amplitudę i częstość kołową drgań.
Wychylenie i prędkość w ruchu harmonicznym wyrażają wzory:
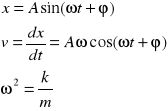
związek między x i v
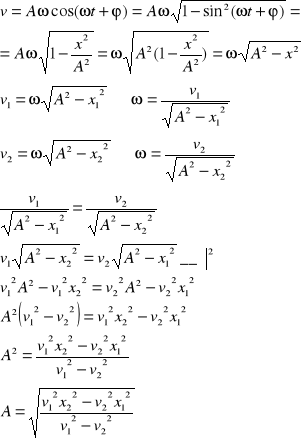
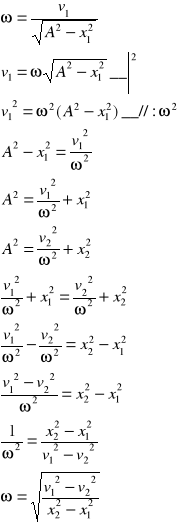
2/IV obliczyć okres małych drgań wahadła matematycznego o długości l=20cm. Kulka wahadła zanurzona jest w idealnej cieczy o gęstości 3 razy mniejszej od gęstości kulki.

3/IV jaki jest stosunek energii kinetycznej punktu drgającego harmonicznie do jego energii potencjalnej w chwilach czasu ![]()
(T-okres drgań). Faza początkowa drgania równa się zero.
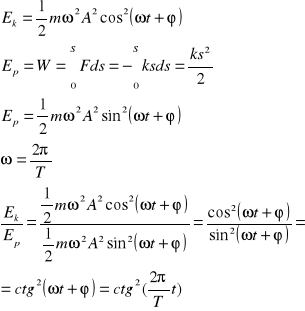
4/IV na gładkiej powierzchni znajduje się ciało o masie M. zamocowane do poziomo ustawionej sprężyny o masie m. i współczynniku sprężystości k. Sprężyna drugim końcem przymocowana jest do pionowej ściany. Obliczyć okres małych drgań.
Faza (ωt+φ) jest równa dla wszystkich punktów sprężyny i klocka. Różna jest natomiast amplituda A.
![]()
obliczamy energie ruchu harmonicznego dla elementu dx
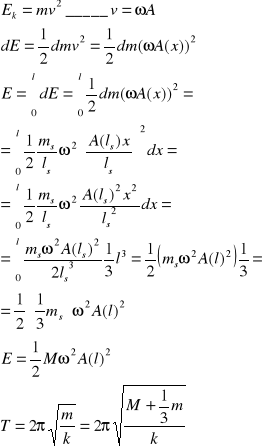
5/IV znaleźć okres drgań półkuli o promieniu R względem osi leżącej w środku płaskiej części i prostopadłej do promienia kuli.
Podzielimy półkulę na bardzo cienkie warstewki będące walcami o promieniu x i wysokości dy. Oś y układu współrzędnych przechodzi przez środki tych walców.
Masa pojedynczej warstewki wynosi:
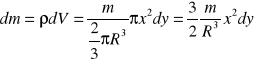
środek masy rozpatrywanej bryły można wyznaczyć z:
S(x0,y0,z0)
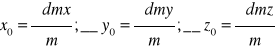
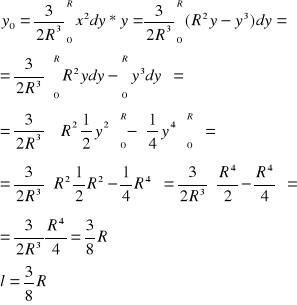
moment bezwładności kuli
![]()
po scałkowaniu
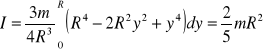
układ stanowi wahadło fizyczne o okresie:
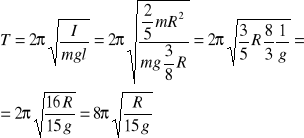
6/IV Na szalkę o masie M zawieszoną na sprężynie o współczynniku sprężystości k z wysokości h spada ciężarek o masie m i pozostaje na niej, wskutek czego szalka wraz z ciężarkiem zaczyna drgać ruchem harmonicznym. Znaleźć amplitudę tych drgań. Rozpatrzyć też przypadek, gdy masę szalki zaniedbujemy.
W przypadku, gdy szalka jest nieważka, wystarczy skorzystać z zasady zach. Energii. Jeśli oznaczyć przez d - dynamiczne odkształcenie sprężyny to mamy:

w celu otrzymania A drgań należy od d odjąć statyczne odkształcenie sprężyny s (gdyż położenie równowagi szalki obciążonej znajduje się o s niżej szalki nieobciążonej)
odkształcenie statyczne ![]()
poszukiwanie amplitudy drgań szalki z ciężarkiem oraz jej okres
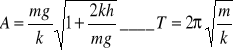
w przypadku o masie m należy skorzystać z zasady zachowania pędu, gdyż zderzenia są niesprężyste.
Jeśli oznaczyć prędkość odważnika w chwili uderzenia o szalkę ![]()
to na podstawie tej zasady:
![]()
po zderzeniu można skorzystać z zasady zachowania energii mech.
![]()
![]()
- odkształcenie sprężyny pod ciężarem szalki
dynamiczne odkształcenie sprężyny wynosi:
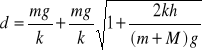
poszukiwana amplituda drgań i okres
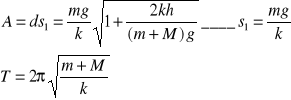
7/IV Aerometr w kształcie walca o powierzchni przekroju S i masie m. jest zanurzony w dwóch niemieszających się cieczach o gęstościach ρ1 i ρ2 w taki sposób, że w stanie równowagi w każdej cieczy znajduje się połowa aerometru. Obliczyć okres drgań aerometru.
W stanie równowagi: x=0
FW1=ρ1ρsa
FW2=ρ2ρsa
Z prawa Archimedesa
Fw=ρρV
Fw=Fw1+FW2
Fw=ρ1ρsa+ ρ2ρsa
II zasada Newtona
mg= ρ1ρsa+ ρ2ρsa
mg=saρ(ρ1+ ρ2)=0
w pozycji wychylenia
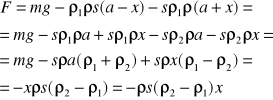
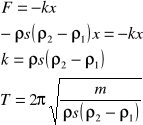
8/IV na trzech nieważkich gumkach o stałych sprężystości k1,k2,k3, połączonych jak na rysunku wisi ciężarek o masie m. ciężarek wytrącono z położenia równowagi tak, iż drga ruchem harmonicznym w kierunku pionowym. Obliczyć okres tych drgań.
Gumki połączone równolegle: k2,3=k2+k3
Gumki połączone szeregowo
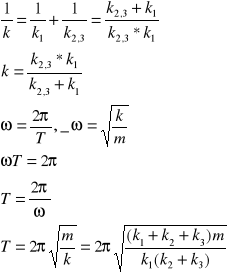
Wyszukiwarka
Podobne podstrony:
ZESTAW 3, Księgozbiór, Studia, Fizyka
ZESTAW 5, Księgozbiór, Studia, Fizyka
06 Badanie zaleznosci sily, Księgozbiór, Studia, Fizyka
metoda Bragga, Księgozbiór, Studia, Fizyka
Kopia cechowanie termopary, Księgozbiór, Studia, Fizyka, Biofizyka
Drgania har. -Aga, Księgozbiór, Studia, Fizyka
Wyznaczanie energii maksymalnej promieniowania beta, Księgozbiór, Studia, Fizyka
IS1, Księgozbiór, Studia, Fizyka
Analiza spr, Księgozbiór, Studia, Fizyka
LABFIZ08, Księgozbiór, Studia, Fizyka
bragg, Księgozbiór, Studia, Fizyka
Kopia hematokryt, Księgozbiór, Studia, Fizyka, Biofizyka
rezyst, Księgozbiór, Studia, Fizyka
więcej podobnych podstron