Grupowanie wariancyjne
W tej metodzie należy zbudować dla badanej cechy schemat klasyfikacyjny o równych co do rozpiętości przedziałach klasowych a następnie przyporządkować poszczególnym klasom jednostki danej zbiorowości.
Procedura grupowania:
Sporządź wykaz wariantów badanej cechy,
Uporządkuj warianty cechy rosnąco (lub malejąco),
Ustal obszar zmienności (rozstęp) badanej cechy:
![]()
Określ liczbę klas (przedziałów klasowych) z jakiej składać się ma schemat klasyfikacyjny dla badanej cechy - k
Liczba ta zawiera się najczęściej w przedziale: ![]()
.
Można ją ustalić w oparciu o następujące zestawienie:
N |
k |
do 30 30 - 40 40 - 60 60 - 100 100 - 200 200 - 500 powyżej 500 |
4 4 - 5 4 - 6 5 - 8 7 - 10 9 - 12 10 - 15 |
Są również podejścia inne, bardziej sformalizowane
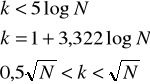
Oblicz rozpiętość przedziału klasowego - h:
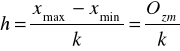
Określ granice przedziałów klasowych
dolna granica pierwszego przedziału powinna być mniejsza od minimalnego poziomu cechy, czyli
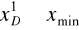
górna granica ostatniego (k - tego) przedziału powinna być wyższa od maksymalnego poziomu cechy, czyli
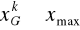
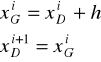
gdzie: i = 1, 2, ..., kprzyporządkowanie poszczególnych wariantów cechy do określonego przedziału musi być jednoznaczne.
Są trzy sposoby określania granic przedziałów:
sposób klasyczny (matematyczny)
przedziały otwarte górą (zamknięte dołem)
przedziały otwarte dołem (zamknięte górą)
Wykonaj część techniczną - przyporządkuj poszczególnym klasom jednostki statystyczne
Opisz skonstruowany szereg statystyczny:
podaj tytuł szeregu,
podaj tytuły kolumn,
pod szeregiem zapisz źródło danych.
Oceń poprawność zbudowanego szeregu statystycznego.
jednomodalność (jedno maksimum) i brak skrajnej asymetrii,
brak klas pustych,
możliwie najbliższy symetryczności,
minimalizacja różnicy między średnią arytmetyczną wyliczoną z danych jednostkowych i średnią arytmetyczną wyliczoną w oparciu o zbudowany szereg.
Zbudowany szereg przedstaw graficznie - histogram (wykres kolumnowy).
Ustalamy obszar zmienności badanej cechy:
Proponujemy k = 6
Ustalamy rozpiętość przedziałów klasowych
Określamy granice przedziałów klasowych, przykładowo:
Kolejne jednostki przyporządkujemy do właściwych przedziałów klasowych zgodnie z zasadą, że jeżeli jednostka ma poziom cechy równy granicy, to należy do
Zbudowany szereg opisujemy i ostatecznie otrzymujemy:
Szereg spełnia warunki wymienione w przedstawionej wcześniej procedurze.
jest jednomodalny, nie jest skrajnie asymetryczny,
nie ma klas pustych,
jest zbliżony do symetrycznego
średnia wyliczona z danych jednostkowych wynosi 202,21 godz.,
nazwa cechy |
środki przedziałów
|
10 - 20 20 - 30 30 - 40 itd. |
15 25 35 .. |
W tym przypadku:
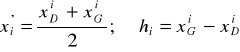
nazwa cechy |
środki przedziałów
|
10 - 19 20 - 29 30 - 39 itd. |
15 25 35 .. |
W tym przypadku:
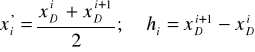
nazwa cechy |
środki przedziałów
|
11 - 20 21 - 30 31 - 40 itd. |
15 25 35 .. |
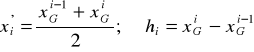
Warunki, które musi taki szereg spełniać:
Przykład :
W przedsiębiorstwie „A” w Poznaniu w październiku 2008 r. przeprowadzono badanie pracowników według czasu pracy przepracowanego we wrześniu w godz.
186 207 202 198 198 191 223 204 196 194 187 203 208 200 192 201 212 206 190 227 203 199 203 217 212 200 214 189 209 197 194 224 206 200 187 204 214 192 220 183 189 219 197 223 210 172 213 210 204 234 180 206 199 190 207 221 195 210 195 192 169 186 203 220 197 191 176 189 230 210 199 206 227 172 202 194 184 200 223 175 188 215 225 182 198 205 234 179 204 195 208 218 180 216 214 230 210 190 211 208
Zbuduj szereg prezentujący strukturę pracowników tego przedsiębiorstwa według czasu pracy przepracowanego we wrześniu (w godz.) stosując grupowanie wariancyjne.
1. Porządkujemy warianty badanej cechy rosnąco:
169 172 172 175 176 179 180 180 182 183 184 186 186 187 187 188 189 189 189 190 190 190 191 191 192 192 192 194 194 194 195 195 195 196 197 197 197 198 198 198 199 199 199 200 200 200 200 201 202 202 203 203 203 203 204 204 204 204 205 206 206 206 206 207 207 208 208 208 209 210 210 210 210 210 211 212 212 213 214 214 214 215 216 217 218 219 220 220 221 223 223 223 224 225 227 227 230 230 234 234
N = |
100 |
|
xmax = |
234 |
|
xmin = |
169 |
|
Ozm = |
234 - 169 = 65 |
|
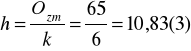
; przyjmijmy więc h = 10
160 - 170 |
170 - 180 |
180 - 190 |
190 - 200 |
200 - 210 |
210 - 220 |
220 - 230 |
230 - 240 |
tego przedziału, którego to jest granica górna (taka zasada przyjęta jest w Excellu)
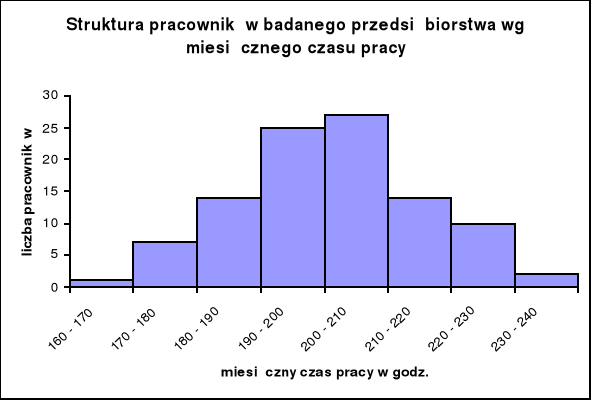
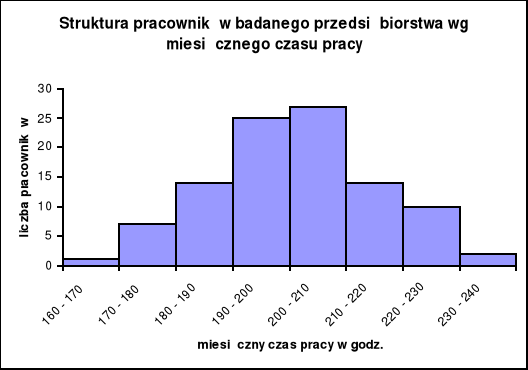
Struktura pracowników badanego przedsiębiorstwa wg miesięcznego
czasu pracy w godzinach przepracowanego we wrześniu 2008 r.
Miesięczny czas pracy w godz. |
Liczba pracowników |
160 - 170 170 - 180 180 - 190 190 - 200 200 - 210 210 - 220 220 - 230 230 - 240 |
1 7 14 25 27 14 10 2 |
Ogółem |
100 |
Źródło: Dane z zadania 1.
średnia wyliczona w oparciu o zbudowany szereg wynosi 201,20 godz.
9. Sporządzamy wykres szeregu:
Wyszukiwarka
Podobne podstrony:
Grupowanie, UG - wzr, I semestr Zarządzanie rok akademicki 11 12, I sem. - Statystyka Opisowa i Ekon
STATYSTYKA OPISOWA '
1 Statystyka opisowa Wprowadze Nieznany (2)
Gorgol I Elementy statystyki opisowej
egzamin ze statystyki, Statystyka opisowa
ROZDZIAŁ 4, Statystyka opisowa
Parametry stosowane w statystyce opisowej, Płyta farmacja Bydgoszcz, statystyka, pozostałe
STATYSTYKA OPISOWA 6 11 2010
Statystyka opisowa wykład interpretacje
1 2 statystyka opisowaid 10222 Nieznany
Przykłady do rozwiązania - tablica korelacyjna, Informatyka i Ekonometria SGGW, Semestr 2, Statystyk
WZORY(1), UEP lata 2014-2019, Statystyka opisowa
więcej podobnych podstron