Ćwiczenia 14. Twierdzenie Koeniga ![]()
(a) - 55 -
Przykład 53
Jednorodny krążek kołowy o masie m = 22 kg i promieniu r = 0.35 m obraca się wokół swej osi geometrycznej ze stałą prędkością kątową, wykonując n = 10 obr/s. Wyznaczyć energią kinetyczną krążka.
r
C ω
Rys. 53
Rozwiązanie
Dla VC = 0 wzór (a) ma postać ![]()
gdzie l jest osią obrotu krążka
a Il momentem bezwładności krążka względem osi l ![]()
![]()
![]()
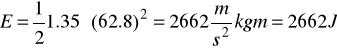
Odpowiedz: Energia krążka wynosi 2662 dżuli
Przykład 54
Jednorodny krążek o promieniu r = 20 cm i masie m = 2 kg toczy się bez poślizgu po poziomej prostej, przy czym prędkość jego środka C równa jest VC = 20 cm/s (rys.54).
Wyznaczyć wartość energii kinetycznej krążka.
C VC ω
Rys. 54
A
Rozwiązanie
![]()
stąd ![]()
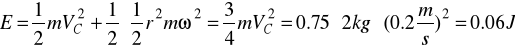
Przykład 55 - 56 -
Na bęben, który może obracać się bez tarcia wokół poziomej osi, nawinięto wiotką i nierozciągliwą linę, na której końcu zawieszono ciało o masie m = 8 kg (rys.55). Należy obliczyć prędkość tego ciała, gdy opuści się ono z wysokości równej h = 0.3m. Promień bębna r = 5 cm, masa bębna M = 2 kg. Masę liny pominąć.
r
C ω
Rys. 55
V = 0
mg h
V = ωr
Rozwiązanie
![]()
gdzie ![]()
jest przyrostem energii układu, W jest pracą sił zewnętrznych
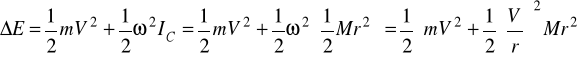
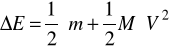
; ![]()
stąd
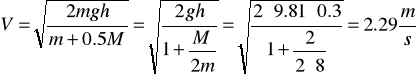
Przykład 56
Cienki jednorodny pręt OA o długości l i masie m może obracać się bez tarcia wokół poziomej osi prostopadłej do osi pręta i przechodzącej przez jego koniec O. Pręt wychylono z położenia równowagi i ustawiono w ten sposób, że jego oś zajmowała położenie poziome i następnie oswobodzono. Obliczyć jaką będzie miał prędkość koniec A pręta w chwili gdy oś pręta będzie tworzyła z poziomem kąt α (rys.56).
Rozwiązanie
A
0 C V = 0 h =0.5 lsinα
h W = mgh =0.5 mglsinα
α 0A = l
mg 0C = CA = 0.5l
V Rys.56
![]()
; ![]()
; ![]()
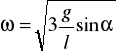
![]()
Wyszukiwarka
Podobne podstrony:
cwiczeniadynamika12, MBM PWr W10, I stopień, mechanika
cwiczeniadynamika13, MBM PWr W10, I stopień, mechanika
cwiczeniadynamika9, MBM PWr W10, I stopień, mechanika
dynamikawyklad12, MBM PWr W10, I stopień, mechanika
dynamikawyklad15, MBM PWr W10, I stopień, mechanika
sciagi z automatow, MBM PWr W10, I stopień, podstawy automatyki
chemia 23, MBM PWr W10, I stopień, chemia
Fiz 1, MBM PWr W10, I stopień, fizyka
Elektr L-ca zal og, MBM PWr W10, I stopień, elektrotechnika
Projekt-z-hartowania-stali-1, MBM PWr W10, II stopień, projektowanie materiałów inżynierskich
projekt 3, MBM PWR, Magisterskie, Synteza mechanizmów, Projekty, projekty inne2
Koła 2010, pwr, air, semestr 3, Mechanika analityczna, KOŁO ĆWICZENIA (matek sp)
więcej podobnych podstron