1. Cel ćwiczenia

Wyznaczenie zależności współczynnika złamania światła od stężenia roztworu za pomocą refraktometru Abbego.

Przy pomocy refraktometru Abbego należało wyznaczyć współczynnik załamania światła dla ośmiu roztworów gliceryny o różnych stężeniach.. Pomiar dokonywany był trzykrotnie dla każdego roztworu a następnie była obliczana średnia wartość owych pomiarów. Kolejnym etapem było wyznaczenie kąta granicznego dla każdego roztworu przy pomocy wzoru sin α= 1/n. Dzięki tablicom matematycznym odczytywany był wynik, czyli wielkość kąta granicznego dla poszczególnych wartości otrzymywanych z wzoru. Ostatnią czynnością było sporządzenie wykresu zależności współczynnika załamania światła od stężenia roztworu i na jego podstawie odczytanie stężenia roztworu „cx” dla wartości współczynnika n =1,346.

2. Wstęp teoretyczny.

Refraktometr Abbego

Refraktometr Abbego w najprostszym wykonaniu składa się z dwóch prostokątnych, pryzmatów ze szkła o dużym współczynniku załamania. Między te pryzmaty wprowadzamy kilka kropel badanej cieczy, której współczynnik załamania powinien być mniejszy niż współczynnik załamania szkła. Ciecz tworzy między przeciwprostokątnymi powierzchniami obu pryzmatów cienką, płasko-równoległą warstewkę, na którą padają pod różnymi kątami promienie wychodzące z pryzmatu P1. Część tych promieni ulega całkowitemu odbiciu na powierzchni cieczy, część zaś przechodzi dalej, przenika pryzmat P2 i opuszcza go nie zmieniając pierwotnego kierunku. Wszystkie promienie padające pod kątem, większym od granicznego ulegają całkowitemu odbiciu. Dzięki takiemu biegowi promieni pole widzenia lunetki podzielone jest na dwie części -- jasną i ciemną, oddzielone od siebie ostrą linią graniczną (oczywiście pod warunkiem użycia światła monochromatycznego). Przez ustawienie lunetki tak, aby umieszczony w płaszczyźnie ogniskowej obiektywu krzyż znalazł się na linii granicznej, odczytać możemy wartość kąta granicznego a następnie obliczyć współczynnik załamania światła badanej cieczy. Posługiwanie się zwykłym refraktometrem Abbego wymaga stosowania światła monochromatycznego (zwykle żółtego światła sodu), gdyż przy stosowaniu światła białego występuje zjawisko rozszczepienia światła, czyli dyspersji. Kąt graniczny jest dla każdej długości fali inny; dlatego to przy użyciu światła niejednorodnego mielibyśmy nie ostrą linię graniczną, lecz rozmytą smugę o barwach tęczy.
      Uniwersalny refraktometr Abbego, pozwala na użycie światła białego- dzięki dodatkowym kompensującym dyspersję urządzeniom. Za jego pomocą mierzy się współczynniki załamania substancji.

Przykładowy schemat refraktometru Abbego przedstawia rysunek.

Dyspersja to zjawisko polegające na rozszczepieniu wiązki światła składającej się z fal o różnych częstotliwościach na wyraźnie oddzielone od siebie fale. Przyczyną rozszczepienia światła jest zależność współczynnika załamania światła od częstotliwości fali świetlnej. Każdej barwie odpowiada inna częstotliwość fali. Ponieważ każda barwa ma inną częstotliwość fali, to każda załamuje się pod innym kątem, dzięki czemu mogą się rozdzielić. Strumień światła zawierający fale o takiej samej częstotliwości nazywamy światłem monochromatycznym (jednobarwnym). Dla światła monochromatycznego zjawisko dyspersji nie występuje.

Zachowanie się promieni świetlnych na granicy dwóch ośrodków opisują prawa odbicia i załamania światła .

1. Promień padający , odbity i załamany oraz normalna

do powierzchni granicznej leżą w jednej płaszczyźnie .

2. Kąt padania
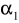
   jest równy kątowi odbicia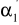
   .

3. Stosunek sinusa kąta padania do sinusa kąta

załamania jest wielkością stała :

gdzie n jest współczynnikiem załamania światła ośrodka 2 do którego promień wchodzi, względem ośrodka 1, z którego wychodzi .

Udowodniono dodatkowo, że współczynnik załamania wyraża się stosunkiem prędkości światła w obu ośrodkach .

n_1,2 = v₁ / v₂

v₁ - prędkość światła w ośrodku 1 , v₂ - prędkość światła w ośrodku 2 .

3. Obliczenia

Roztwór: Woda destylowana

Stężenie: 0 g/cm³

Średni współczynnik załamania (n): (1,332+1,332+1,332)/3= 1,332

Kąt graniczny: sin α_g= 1/n

Sin α_g= 1/1,332= 0,751 sin 0,751≈ 48^o42'

Roztwór:1

Stężenie: 0,05 g/cm³

Średni współczynnik załamania (n): (1,339+1,339+1,339)/3= 1,339

Kąt graniczny: sin α_g= 1/1,339= 0,747

Sin 0,747 ≈ 48 ^o24'

Roztwór:2

Stężenie: 0,1 g/cm³

Średni współczynnik załamania (n): (1,344+1,344+1,344)/3= 1,344

Kąt graniczny: sin α_g= 1/1,344= 0,744

Sin 0,744 ≈ 48 ^o6'

Roztwór:3

Stężenie: 0,15 g/cm³

Średni współczynnik załamania (n): (1,349+1,350+1,349)/3= 1,349

Kąt graniczny: sin α_g= 1/1,349= 0,741

Sin 0,741 ≈ 47 ^o48'

Roztwór:4

Stężenie: 0,2 g/cm³

Średni współczynnik załamania (n): (1,355+1,355+1,355)/3= 1,355

Kąt graniczny: sin α_g= 1/1,355= 0,738

Sin 0,738 ≈ 47 ^o36'

Roztwór:5

Stężenie: 0,25 g/cm³

Średni współczynnik załamania (n): (1,359+1,359+1,359)/3= 1,359

Kąt graniczny: sin α_g= 1/1,359= 0,736

Sin 0,736 ≈ 47 ^o24'

Roztwór:6

Stężenie: 0,3 g/cm³

Średni współczynnik załamania (n): (1,365+1,365+1,365)/3= 1,365

Kąt graniczny: sin α_g= 1/1,365=0,733

Sin 0,733 ≈ 47 ^o6'

Roztwór:7

Stężenie: x g/cm³

Średni współczynnik załamania (n): (1,346+1,345+1,346)/3= 1,346

Kąt graniczny: sin α_g= 1/1,346= 0,743

Sin 0,743 ≈ 48 ^o0'

4. Wnioski i spostrzeżenia

Wartość współczynnika n zależy od stężenia roztworu. Wartość jego rośnie wraz ze wzrostem stężenia roztworu. Inaczej jest z wartością kąta granicznego- jest on odwrotnie proporcjonalny do współczynnika n, czyli wraz ze wzrostem stężenia roztworu i współczynnika załamania, wartość kąta granicznego maleje.

Dokonane pomiary za pomocą refraktometru pozwoliły również na określenie stężenia roztworu cx. Rysowanie wykresu zależności średniego współczynnika załamania światła dla roztworów o określonym stężeniu pozwoliło na odczytanie wyniku dla współczynnika o wartości 1,346- jest to roztwór o stężeniu 0,120 g/cm³

5. Literatura

• http://translate.google.pl/translate?hl=pl&langpair=en|pl&u=http://www.ue-soft.de/oilfield/techtabs/mathe/mathe005.pdf - tablice matematycze

Fizyka od A do Z repetytorium; Andrzej Wasiak, Wydawnictwo Kram

http://www.bartekt0.siemce.pl/artykuly/abbe/abbe.html- refraktometr Abbego

3

---