PROSTA EKSTRAPOLACJA TRENDU

Prognozowanie ma na celu przewidywanie przyszłości w sposób racjonalny z wykorzystaniem metod naukowych. Ze względu na różne typy czynników poddawanych prognozowaniu i różne sytuacje, w których prognozy są potrzebne, nie ma jednej uniwersalnej metody. Do sporządzania różnorodnych prognoz menedżerowie wykorzystują kilka różnych sposobów. Najbardziej rozpowszechnione są metody ilościowe (statystyczne), określające prawdopodobieństwo przyszłych zdarzeń na podstawie danych historycznych. W ramach metod ilościowych jest dostępnych wiele technik wnioskowania, np. analiza szeregów czasowych, na podstawie której można wyznaczyć trend. Znajomość tendencji rozwojowej badanego zjawiska umożliwia ekstrapolację dotychczasowych prawidłowości na pewien, niezbyt odległy okres w przyszłości. Aby jednak oparta na tej metodzie prognoza była trafna (z zachowaniem pewnych granic błędu), muszą zostać spełnione założenia dotyczące trendu.

OKREŚLENIE TRENDU

Trend, zwany tendencją rozwojową to długookresowa tendencja powodująca systematyczny wzrost lub spadek obserwowanych w szeregu czasowym wielkości. Bada się ją zwykle w okresach 10 i więcej lat. Ponieważ tendencja rozwojowa jest rozpatrywana jako rezultat działania stałego zestawu czynników, warunkiem doboru okresu badania jest działanie tych samych przyczyn głównych. Dla przykładu można tu wymienić postęp technologiczny, zmiany w liczbie ludności, zmiany zamożności, preferencje konsumentów. Czynniki te mogą powodować jednokierunkowe zmiany w obserwowanych wielkościach, charakteryzują się pewną prawidłowością, co umożliwia wyznaczenie trendu.
Aby określić charakter tendencji rozwojowej, należy nanieść odnotowane wartości badanej zmiennej w układ współrzędnych, gdzie na osi X oznaczone są momenty czasu, dla których odnotowano poszczególne wartości. Nie oznacza to, że czas stanowi przyczynę występowania określonej tendencji rozwojowej. Określa on jedynie wpływ bezpośrednio nieznanych czynników i stwarza możliwość opisu zmian w sposób ilościowy.
Jeżeli otrzymany układ punktów jest najbardziej zbliżony do wykresu linii prostej, to mówimy o trendzie prostoliniowym w kształtowaniu się danego zjawiska. Jeżeli zaś układ punktów ma kształt inny niż prostoliniowa postać funkcji, to możemy mówić o trendzie krzywoliniowym, w przypadku którego w pewnych okresach mogą występować wzrosty, a w innych spadki wartości rozpatrywanej zmiennej. Zakłócenia ogólnej tendencji rozwojowej są spowodowane działaniem tzw. przyczyn ubocznych oraz występowaniem wahań przypadkowych lub sezonowych.
Założenia prognozowania na podstawie trendu:

- istnieje dostatecznie dużo danych źródłowych, pochodzących z obserwacji czynionych w regularnych odstępach, przez dłuższy okres czasu,
- prognozowane zjawisko ma charakter mierzalny,
- występują ciągłe, powtarzalne i regularne zmiany badanego zjawiska,
- występuje długookresowa, w miarę trwała i stabilna prawidłowość w kształtowaniu się danej zmiennej,
- skłonność do jednokierunkowych zmian (wzrostu lub spadku) wartości badanej zmiennej jest konsekwencją działania stałego zestawu czynników tzw. przyczyn głównych,
- prognozowane zjawisko charakteryzuje się dużą inercją,
- tendencja kształtuje się w stabilnym otoczeniu, dotyczy obszaru o małej dynamice,
- zaobserwowana w minionym okresie tendencja rozwojowa będzie zachowana również w przyszłości,
- w okresie, na który jest budowana prognoza, przyczyny główne będą działały w tym samym kierunku i z podobnym natężeniem jak dotychczas,
- wpływ czynników przypadkowych będzie zbliżony.

Prognozowanie w oparciu o trend jest dokładniejsze im:
- dłuższy okres uwzględniamy w badaniu tendencji rozwojowej, im większa jest baza danych dotycząca kształtowania się trendu
- powolniejsze są zmiany prognozowanej wielkości wskutek oddziaływania postępu technologicznego, organizacyjnego i ekonomicznego
- bardziej autonomiczny charakter mają prognozowane wielkości, a więc im mniejsze jest uzależnienie ich od decyzji strategicznych
- wyższy jest stopień inercji prognozowanej zmiennej- im powolniejsze są zmiany ilościowe
- bardziej stabilne jest otoczenie, w którym kształtuje się tendencja rozwojowa
krótszy jest horyzont czasowy prognozy- wyprzedzenie czasowe prognozy
Ekstrapolacja trendu

Celem wyodrębnienia trendu, czyli określenia tendencji rozwojowej badanego zjawiska, jest obliczanie wartość charakteryzującej to zjawisko dla określonego, niezbyt długiego czasu. Metodą prognozowania w oparciu o wyznaczoną tendencję jest ekstrapolacja trendu. Metoda ta należy do grupy metod statystyczno-matematycznych i może być stosowana jedynie w odniesieniu do zjawisk mierzalnych, o charakterze powtarzalnym, dla których jesteśmy w stanie określić trend. Warunkiem stosowania ekstrapolacji trendu jest również spełnienie założeń, że zaobserwowana w minionym okresie tendencja rozwojowa będzie zachowana również w przyszłości, oraz że wpływ czynników przypadkowych będzie zbliżony. W takich przypadkach ekstrapolacja trendów pozwala na określenie, z dużym przybliżeniem, zdarzeń i ich rzędu wielkości w określonym czasowym przedziale.
Przewidywanie przyszłości jest w tym przypadku ekstrapolowaniem wykrytych w przeszłości prawidłowości w przyszłość. Polega ono na przedłużeniu kierunku i dynamiki rozwoju zjawiska z okresu, z którego pochodzi obserwacja, na okres prognozowany. Ekstrapolacja trendu w sensie graficznym jest po prostu przedłużeniem linii trendu poza przedział obserwacji.
Zanim jednak dokonamy ekstrapolacji konieczne jest ustalenie na podstawie posiadanych danych linii opisującej trend. W tym celu rozpatrywana zmienna zostaje przedstawiona graficznie jako funkcja czasu, a następnie ustalona jest linia „najlepszego dopasowania”. Najczęściej przyjmowaną postacią funkcji trendu jest funkcja liniowa, jednak jej stosowanie może spowodować duże zniekształcenia w opisie rzeczywistego przebiegu wielkości prognozowanego zjawiska. Prawdziwa prognoza w oparciu o ekstrapolację trendu obejmuje znacznie więcej niż samo tylko naniesienie na wykres danych i następnie przedłużenie linii. Potrzebne są m.in. skomplikowane obliczenia matematyczne, które pozwalają uwzględnić wahania sezonowe i cykliczne oraz zidentyfikować prawdziwą linię najlepszego dopasowania. W rzeczywistych sytuacjach dane rzadko dają się przedstawić za pomocą linii prostej i jedynie użycie programów komputerowych pozwala ujawnić istotne tendencje. Jeżeli prognoza jest opracowana prawidłowo i wszystko przebiega zgodnie z założeniami, to powinna ona dostarczyć zadowalające szacunkowe wartości przyszłego poziomu badanego zjawiska.

METODY WYZNACZANIA TRENDU

Do wyodrębnienia trendu na podstawie danych najczęściej wykorzystuje się dwie metody: mechaniczną i analityczną.

Metoda mechaniczna

Metoda mechaniczna opiera się na średnich ruchomych. Polega ona na obliczaniu średnich arytmetycznych z określonej liczby odnotowanych kolejnych wartości. Przy obliczaniu kolejnych średnich odrzucamy pierwszą wartość, dodajemy następną i ponownie obliczamy średnią z otrzymanej sumy. Otrzymaną w ten sposób wartość przypisujemy środkowemu momentowi. Średnie ruchome mogą być obliczane z nieparzystej liczby wyrazów (średnie ruchome zwykłe), bądź z parzystej (średnie ruchome scentrowane).

Jeśli wartości odnotowane dla kolejnych momentów czasu oznaczymy przez
y1, y2, y3, y4, ... yn to:

- średnie ruchome zwykłe - dla nieparzystej liczby okresów, np. k=3 obliczamy w następujący sposób:

- średnie ruchome scentrowane - dla parzystej liczby okresów, np. k=4 obliczamy następująco:

Przez obliczenie średnich ruchomych eliminujemy z szeregu przypadkowe i okresowe wahania. Im średnia ruchoma obejmuje więcej jednostek czasu, tym linia przedstawiająca przebieg trendu zostaje bardziej wyrównana. Zostają wygładzone wszystkie odchylenia od tendencji rozwojowej. Zaletą tej metody są proste obliczenia i przedstawianie trendu uwolnionego od czynników przypadkowych. Wadą natomiast jest skracanie szeregu wartości opisujących trend. Przykładowo przy średniej ruchomej trzyokresowej szereg skraca się o dwa okresy (jeden na początku i jeden na końcu). Im więcej wartości wykorzystamy do obliczania średniej ruchomej, tym szereg „wygładzony” jest coraz krótszy. Brakuje informacji o wartościach końcowych, które mają największe znaczenie dla ustalenia prognozy. Zmniejsza to praktyczną przydatność tej metody, ponieważ trudniej jest dokonać prawidłowej ekstrapolacji. Mimo to sposób ten jest przydatny, gdy nie ma możliwości doboru do odnotowanych wartości dostatecznie dokładnej funkcji opisującej przebieg trendu.

Przykład wyznaczenia trendu metodą mechaniczną

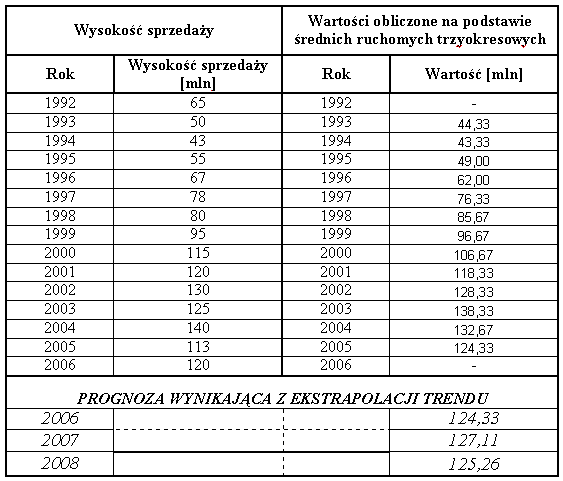
Na podstawie danych zawartych w tabeli wyznaczymy metodą mechaniczną linię trendu i dokonamy jej ekstrapolacji na najbliższe 3 lata. W obliczeniach posłużymy się średnimi ruchomymi trzyokresowymi. Wszystkie obliczenia zostały uwzględnione w tabeli1.

Tabela1. Wysokość sprzedaży firmy XYZ w latach 1992 - 2006.

Używając do prognozowania metody średnich ruchomych, przyjmuje się, że wartość zmiennej prognozowanej w następnym okresie czasu będzie równa średniej arytmetycznej z k ostatnich wartości tej zmiennej (w podanym przykładzie k=3).

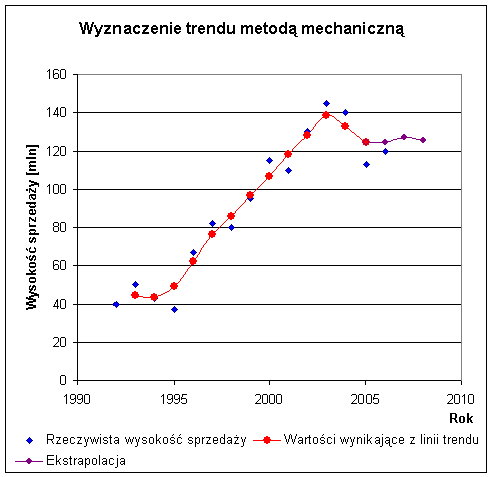
Wykres 1. Wyznaczenie trendu metodą mechaniczną i jego ekstrapolacja.

Metoda analityczna

Metoda analityczna opiera się na naniesieniu w układ współrzędnych danych odnotowanych w kolejnych okresach, a następnie na znalezieniu funkcji, która optymalnie pasuje do wartości. Najprostszy sposób doboru funkcji polega na wzrokowej ocenie ułożenia punktów w układzie współrzędnych i na analizie przyrostów trendu. Tendencja rozwojowa jest najprostsza do określenia, gdy odpowiada jej funkcja liniowa, przedstawiająca sytuację, w której badane zjawisko charakteryzuje się podobnymi wartościami przyrostów lub spadków dla wszystkich okresów. Jednak linia trendu może przebiegać w różny sposób i do jej przedstawienia są stosowane także funkcje wykładnicze, hiperboliczne, krzywe gasnące i inne. Ogólnie zaleca się, aby wybrany typ funkcji był możliwie prosty i posiadał cechy, które charakteryzują rozwój danego trendu. Kolejnym krokiem w tej metodzie jest obliczenie parametrów wybranej funkcji i określenie jej wzoru. Na podstawie wzoru będzie możliwe ustalenie wartości trendu dla przyszłych okresów czasu.

Rodzaje trendu

W zależności od tego, jaka funkcja opisuje kształtowanie się tendencji rozwojowej, możemy wyróżnić podstawowe rodzaje trendów:

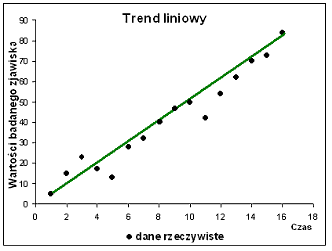
Trend liniowy- jest stosowany, gdy występują zbliżone zmiany (przyrosty lub spadki) poziomu zjawiska w kolejnych okresach.

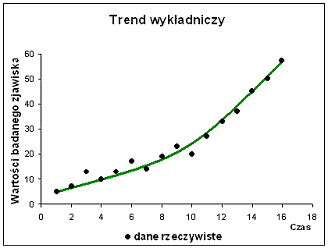
Trend wykładniczy- jest wykorzystywany, gdy zmiany poziomu zjawiska są coraz szybsze, przyrosty odnotowanych wartości są rosnące.

Trend paraboliczny (kwadratowy)- jest wykorzystywany, gdy badane zjawisko najpierw rośnie, a potem maleje, bądź też najpierw spada, a potem wzrasta.

Trend hiperboliczny- znajduje zastosowanie gdy badane zjawisko charakteryzuje się coraz wolniejszymi przyrostami lub spadkami prognozowanej wielkości, zmiany są coraz wolniejsze i dążą do określonego poziomu.

Trend logistyczny- opisuje zjawiska, które najpierw rosną wolno, potem coraz szybciej, a wreszcie tempo wzrostu maleje i następuje stagnacja. Ten rodzaj trendu jest użyteczny w analizie rynku, np. gdy obserwuje się zmiany popytu na towary wprowadzane na rynek.

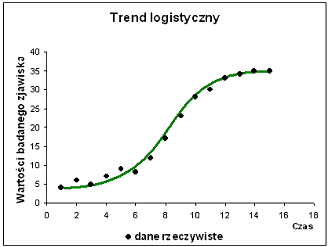
Przykład wyznaczenia trendu metodą analityczną

Najczęściej przyjmowaną postacią funkcji trendu jest funkcja liniowa, która reprezentuje stały kierunek rozwoju danego zjawiska. Rozpatrywana tendencja zostaje przedstawiona jako funkcja czasu, a następnie zostaje określona linia najlepszego dopasowania, od której wyznaczone punkty są najmniej oddalone. Parametry tej liniowej funkcji są obliczane metodą najmniejszych kwadratów (zwykłą lub uproszczoną). Metoda ta ma na celu zmniejszenie odchyleń zaobserwowanych wartości od wyznaczonych za pomocą funkcji. Wzory stosowane do obliczeń funkcji liniowej zostały przedstawione w tabeli2.

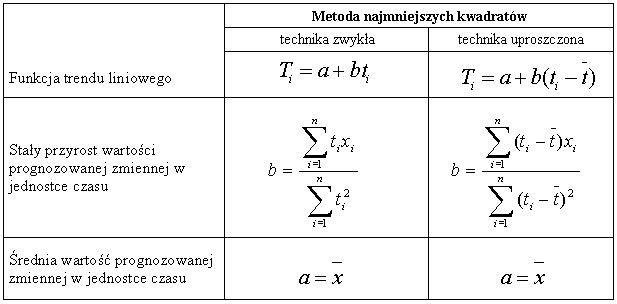
Tabela2. Wzory wykorzystane do wyznaczenia liniowej funkcji trendu.

W technice zwykłej parametr a określa teoretyczną wartość danej zmiennej w okresie bezpośrednio poprzedzającym pierwszy okres analizowanego szeregu czasowego, parametr b natomiast informuje o tym, o ile średnio zmienia się (rośnie lub spada) wartość badanej zmiennej z okresu na okres. Technika uproszczona opiera się na odchyleniach wartości od średnich. Tak więc parametry a i b różnią się jedynie tym że są obliczone dla .
W oparciu o dane zawarte w tabeli wyznaczymy linię trendu, obrazującą tendencję wzrostową sprzedaży i dokonamy jej ekstrapolacji w celu ustalenia prognozy na najbliższe 3 lata.

Przyjmiemy, że rozpatrywana tendencja rozwojowa ma charakter liniowy i w celu wyodrębnienia funkcji trendu wykorzystamy metodę najmniejszych kwadratów (technikę zwykłą). W obliczeniach posłużymy się podanymi wzorami i symbolami uwzględnionymi w tabeli. Kolumna z umowną numeracją lat została wprowadzona dla ułatwienia obliczeń i nie ma ona wpływu na ostateczną wartość współczynników a i b.

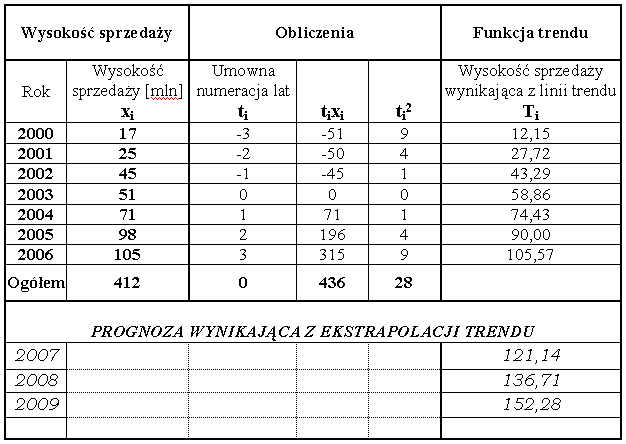
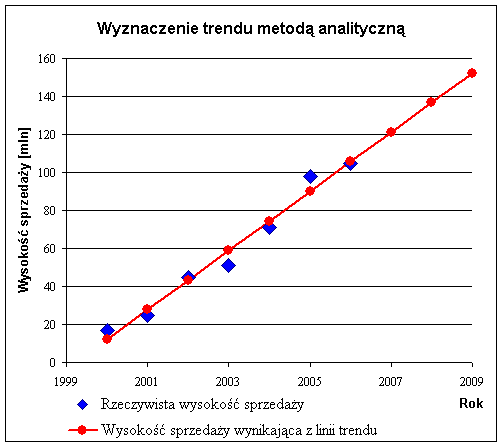
Tabela 3. Wysokość sprzedaży produktów firmy XYZ w latach 2000-2006
Na podstawie wyznaczonego trendu możemy określić prawdopodobną wysokość sprzedaży dla przyszłych trzech lat poprzez przedłużenie linii trendu lub poprzez obliczenie kolejnych wartości w oparciu o funkcję tendencji rozwojowej.
Przykład ten pokazuje, że prognozowanie w oparciu o ekstrapolację trendu wymaga uproszczeń i założeń dotyczących utrzymania się zaobserwowanej tendencji rozwojowej. Prognoza jest obarczona pewnym błędem - różnicą pomiędzy oczekiwanymi a rzeczywistymi wartościami badanego zjawiska.

Wykres 2. Wyznaczenie trendu metodą analityczną i jego ekstrapolacja.
Zakłócenia tendencji rozwojowej

Wyznaczanie trendu utrudniają czynniki przypadkowe, wahania sezonowe i cykliczne, które nakładają się na siebie i powodują odchylenia w kształtowaniu się tendencji rozwojowej. Jeżeli wahania sezonowe i cykliczne wykazują daną prawidłowość możliwe jest ich wyodrębnienie i wówczas są również brane pod uwagę w ustalaniu prognozy.

Przykłady zakłóceń tendencji rozwojowej :

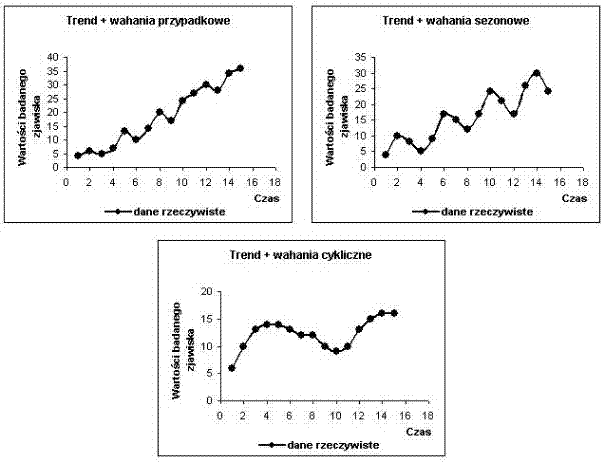
Wady i zalety

Ekstrapolacja trendu umożliwia przewidywanie przyszłości w oparciu o ciąg zdarzeń z przeszłości. Metoda ta może być stosowana przy analizowaniu zjawisk w branżach o małej dynamice rozwoju, funkcjonujących w stabilnym otoczeniu np. przy przewidywaniu zmian w otoczeniu demograficznym, zmian w rozmiarach rynku. Ponieważ prognozowanie na podstawie trendu zakłada, że przeszłość jest dobrą podstawą przewidywania przyszłości, jest ono najbardziej przydatne wtedy, kiedy dane historyczne są dostępne, trendy stabilne, a wzorce wyraźnie dostrzegalne. Jeżeli przewidywania powstają na podstawie rzetelnych danych można ustalić prognozy oparte na względnie obiektywnych metodach. Konstruując taką prognozę, korzysta się z zasady status quo, tzn. przyjmuje się, że w okresie, na który jest budowana prognoza, na prognozowane zjawisko będą oddziaływały te same czynniki otoczenia organizacji i w taki sam sposób jak dotychczas, a realizowana strategia nie ulegnie zmianie. Metoda ta jest więc przydatna przede wszystkim do sporządzania prognoz krótkookresowych, traktowanych jako wstępne przewidywanie przyszłego rozwoju.
Korzystanie z tej metody prognozowania nie gwarantuje, że opracowane prognozy będą niezawodne, natomiast ułatwia dojście do takich prognoz. Trzeba pamiętać, że trend nie opisuje niezmiennych praw natury, a jedynie coś, co działo się do tej pory, nawet przez długi czas, co jednak może zostać zmienione pod wpływem czynników zewnętrznych. Nawet przy najbardziej skomplikowanej technice, wspomaganej przez komputery, rzeczywistość często musi podlegać upraszczaniu. Uogólniona prawidłowość rozwoju wymaga dużej ostrożności i może być dokonana jedynie wycinkowo.
Istnieją także pewne sfery otoczenia, których badanie tymi metodami może być bardziej zawodne i nie przynosić oczekiwanych rezultatów. Dla bardziej dynamicznych obszarów możliwe jest wykorzystanie tej metody jedynie pod warunkiem skrócenia analizowanych odcinków czasowych. Będzie to miało wpływ na wielkość baz danych, a więc na wiarygodność wyników. Stąd ryzykowne jest stosowanie ekstrapolacji trendu w stosunku do zjawisk otoczenia technologicznego, czy też społecznego.
Prognozy nie zawsze dokładnie odzwierciedlają rzeczywistość, bowiem występują zupełnie przypadkowe zakłócenia i zmiany czynników mających wpływ na kształtowanie się trendu. Wiele problemów nie poddaje się analizie ilościowej i nie jest możliwe ich prognozowanie w oparciu o tendencję rozwojową.

---