• Laboratorium fizyki CMF PŁ

• Dzień ............ godzina................ grupa..........

Wydział _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

semestr _ _ _ _ _ _ _ _ _ _ rok akademicki _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

ocena _____

1.Cel ćwiczenia.
Celem ćwiczenia będzie pokazanie przypadku rozchodzenia się fal w ośrodku dwuwymiarowym. Metodę taką opracował pochodzący z Saksonii Chladni. Polegała ona na pobudzaniu do drgań metalowych płyt o różnych kształtach przez przeciąganie smyczkiem po ich krawędzi. Częstotliwościom rezonansowym towarzyszy pojawianie się w ośrodku linii węzłowych. Rozsypując drobnoziarnisty piasek na powierzchni wzbudzonej rezonansowo płyty Chladni uzyskiwał oryginalne wzory linii węzłowych.
Nasze doświadczenie polega na powtórzeniu eksperymentu z taką różnicą, że do pobudzenia metalowych płyt wykorzystamy specjalnej konstrukcji głośnik wibrujący z częstościami akustycznymi, poprawiający stabilność i powtarzalność obserwowanych obrazów.

2.Przebieg ćwiczenia.

Wariant 1:
Po umocowaniu okrągłej tarczy i posypaniu równomiernie jej powierzchni piaskiem, włączyliśmy generator, a następnie przy ustawieniu pokrętła AMPLITUDE w pozycji między MIN, a MAX rozpoczęliśmy powolne obracanie pokrętła ADJUST, odpowiedzialnego za zmianę częstotliwości. Piasek zaczął wyraźnie drgać i zsuwać się do pozycji węzłowych. Notowaliśmy częstotliwości i fotografowaliśmy powstałe obrazy. Eksperyment powtórzyliśmy opcjonalnie dla tarczy kwadratowej.

Oto częstotliwości wraz z obrazkami:
- dla tarczy okrągłej

=> 880 Hz
=> 1650 Hz

- dla tarczy kwadratowej

=> 1890 Hz
=> 1724 Hz








































=> 1400 Hz
=> 1070 Hz

=> 960 Hz
=> 817 Hz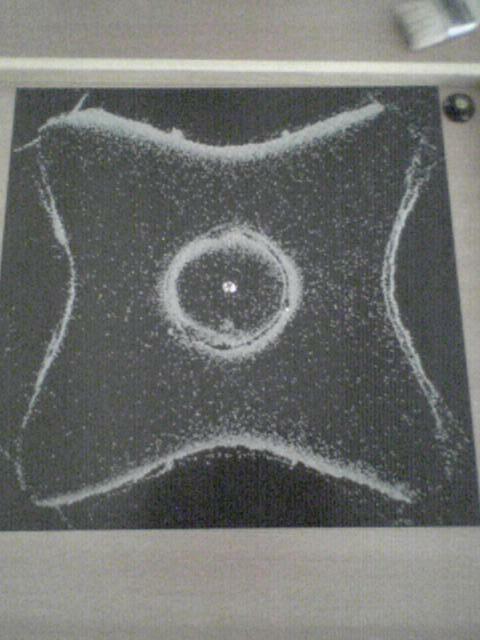












































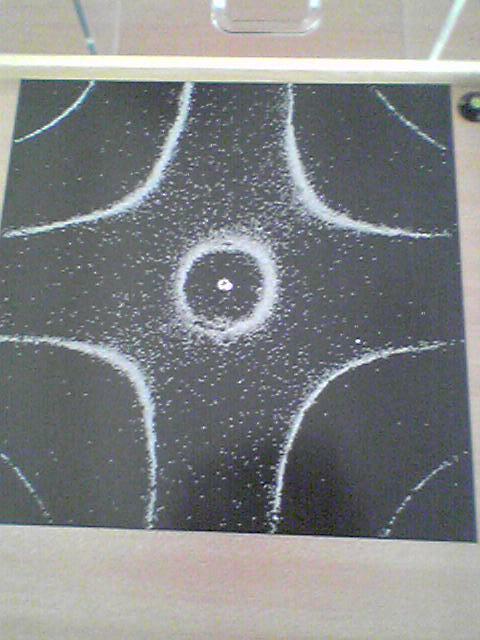
=> 489 Hz
=> 340 Hz

Wariant 2:
Eksperyment jest identyczny, z tą różnicą, że badamy tylko tarczę kołową i wraz ze wzrostem częstotliwości zwiększającą się liczbę okręgów.

Tu są wypisane częstotliwości porównane z ilością okręgów:

Częstotliwość:	Ilość okręgów:
108 Hz	n=3
850 Hz	n=4
1690 Hz	n=5
2677 Hz	n=6
3950 Hz	n=7
5650 Hz	n=8
7485 Hz	n=9
9650 Hz	n=10

3. Rachunki ćwiczeniowe:

Równanie prostej y=ax+b ma następujące parametry:
a= 0.03834
b=36.34147

Δa=0.001
Δb=3.209

Współczynnik korelacji wynosi: 0.99919, co oznacza, że przebieg badanego zjawiska rzeczywiście jest liniowy.

4. Wnioski:
Jeśli chodzi o wariant 1,to wraz ze wzrostem częstotliwości, wzrastała liczba węzłów, a figury stawały się coraz bardziej urozmaicone. W wariancie 2 zaś wraz ze wzrostem częstotliwości wzrastała liczba okręgów, a z rachunków ćwiczeniowych wyszło, że częstotliwość wzrasta proporcjonalnie do pojawiania się kolejnych okręgów na tarczy.

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu _ _ _ _ _ _ _ _ _ _ _ _

Kod ćwiczenia	Tytuł ćwiczenia
M5	Badanie dwuwymiarowych modów drgań metodą figur Chladniego

---