Maria Kotełko

Mechanika

i Wytrzymało

ść

Materiałów

————————————————————————————————————————

Zadanie nr 32 - Dostosowanie kierunku Automatyka i Robotyka

do prowadzenia studiów niestacjonarnych

2

Mechanika i …

Wykład 5.

1. Przestrzenny układ sił zbieżnych

2. Dowolny przestrzenny układ sił

3. Redukcja dowolnego przestrzennego

układu sił

4. Moment siły względem osi

5. Warunki równowagi dowolnego

przestrzennego układu sił

3

Mechanika i …

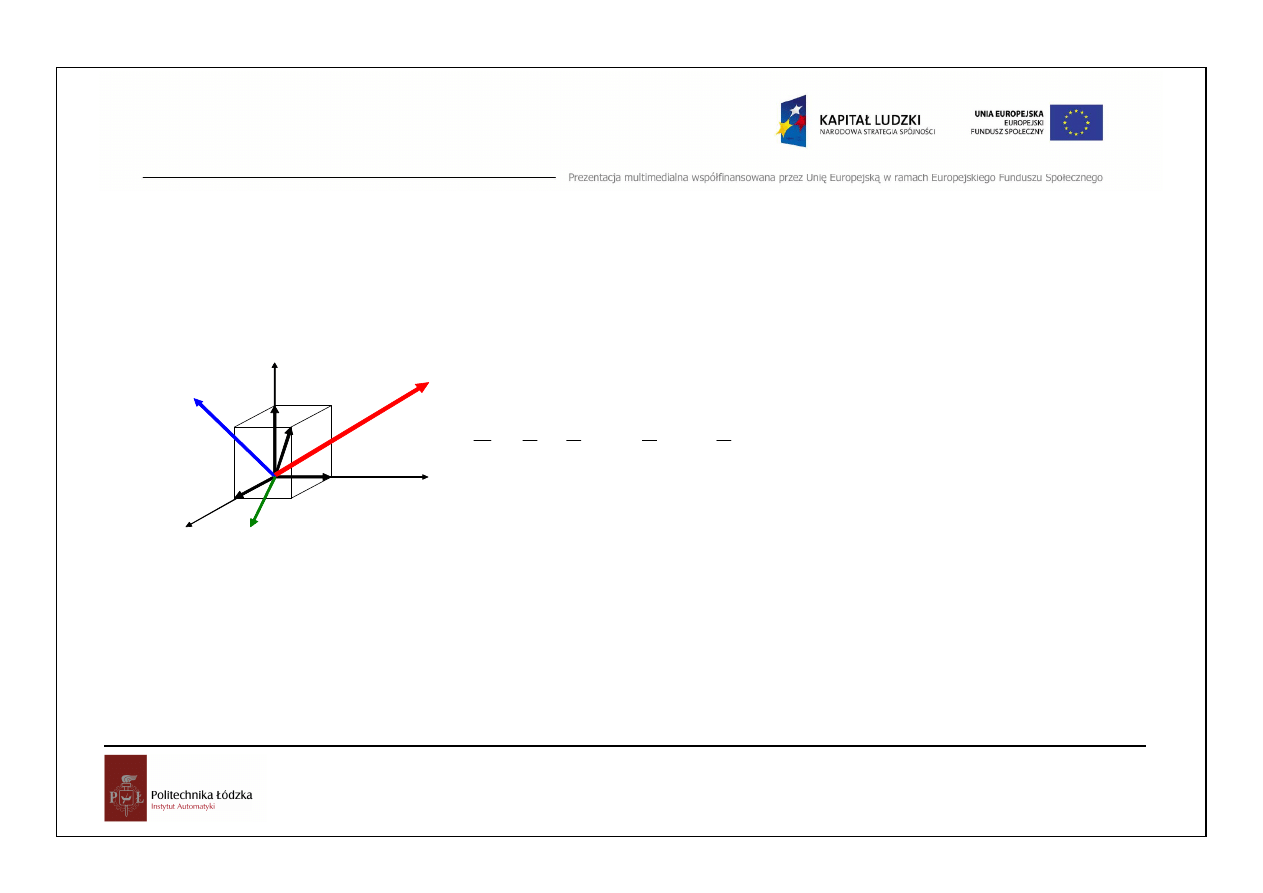
Przestrzenny układ sił zbie

ż

nych

P

i

P

ix

P

iz

P

iy

z

x

y

P

1

R

P

3

R

P

P

P

P

n

i

i

n

= + + + =

=

∑

1

2

1

...

.

Dowolny układ sił przy łożony ch do jednego punktu
zastąp ić możemy jedną siłą wypadkową, przy łożoną w
tymże p unkcie i równą sumie geometrycznej
poszczególnych sił.
Wypadkową tę można wyznaczyć wykorzystując

zasadę równoległościanu

, analogiczną do zasady

równoległoboku.

4

Mechanika i …

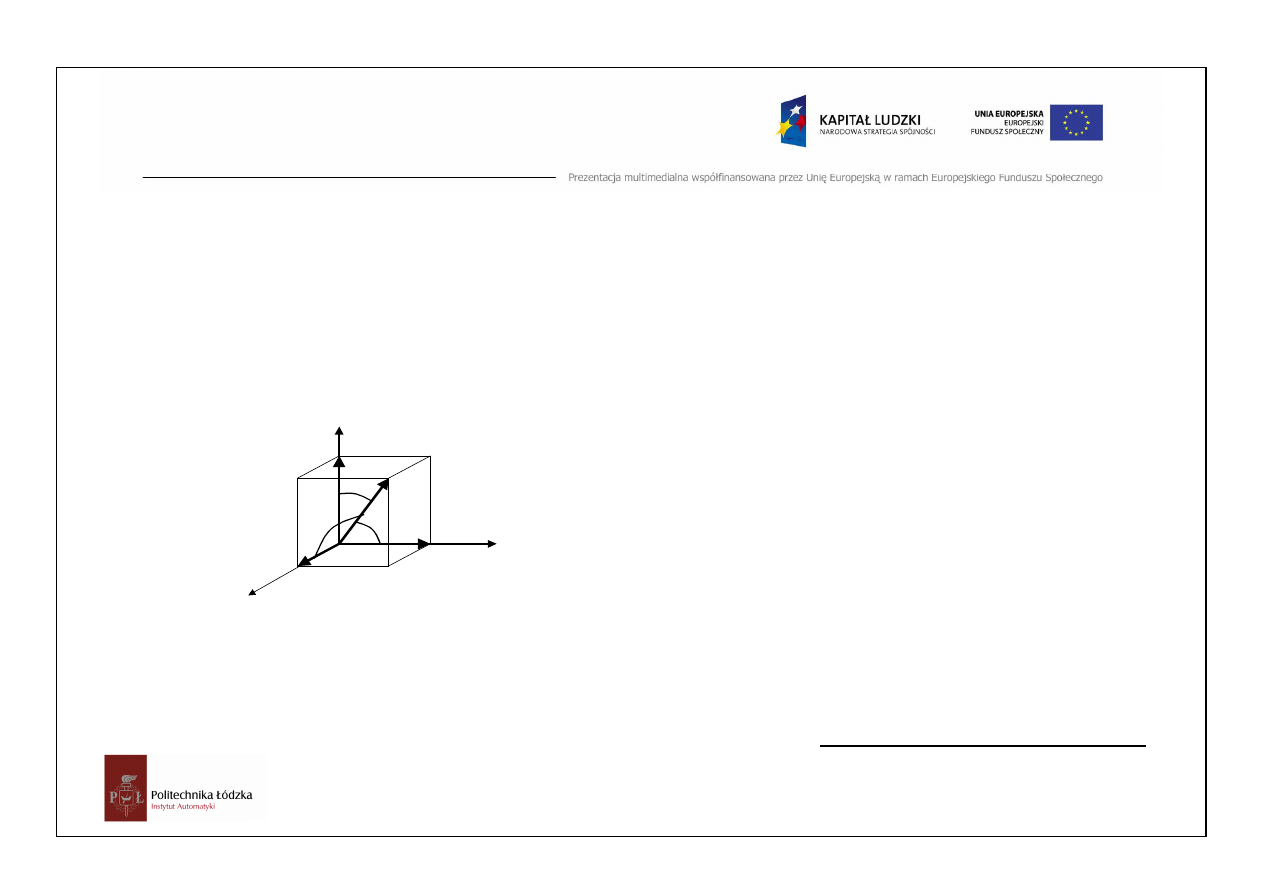
Zasady rzutowania w przestrzeni

P

i

P

ix

P

iz

P

iy

z

x

y

α

αα

α

i

ββββ

i

γγγγ

i

i

i

ix

P

P

α

cos

⋅

=

,

i

i

iy

P

P

β

cos

⋅

=

,

i

i

iz

P

P

γ

cos

⋅

=

5

Mechanika i …

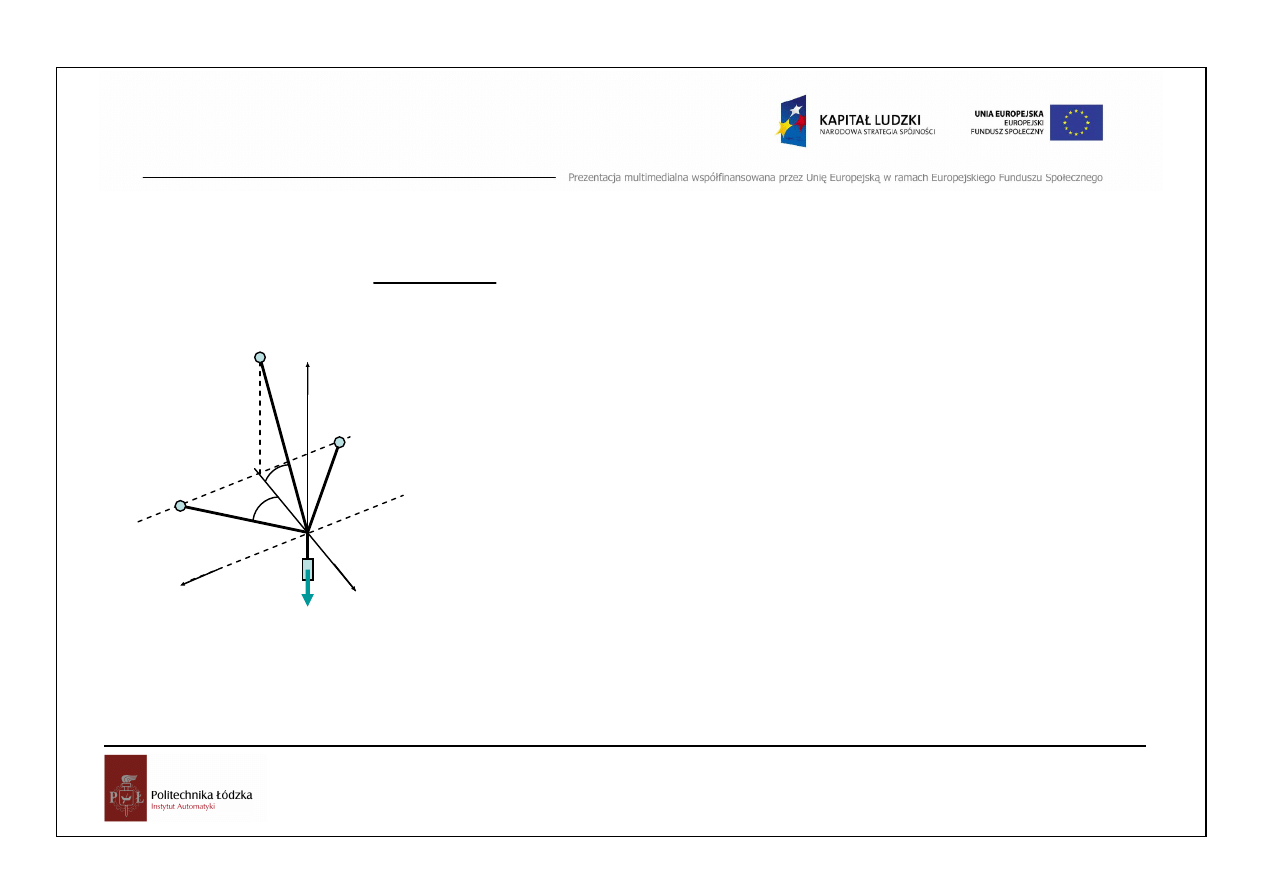
Warunek równowagi przestrzennego układu sił

zbie

ż

nych

P

P

P

P

n

i

i

n

1

2

1

0

+ + + =

=

=

∑

...

Wypadkowa przestrzennego zbieżnego układu sił musi być równa zeru, tj
musi tworzyć zamknięty wielobok sił w przestrzeni.

P

P

ix

i

n

iy

i

n

=

=

∑

∑

=

=

1

1

0

0

P

iz

i

n

=

∑

=

1

0

Warunki równowagi w postaci analitycznej:

6

Mechanika i …

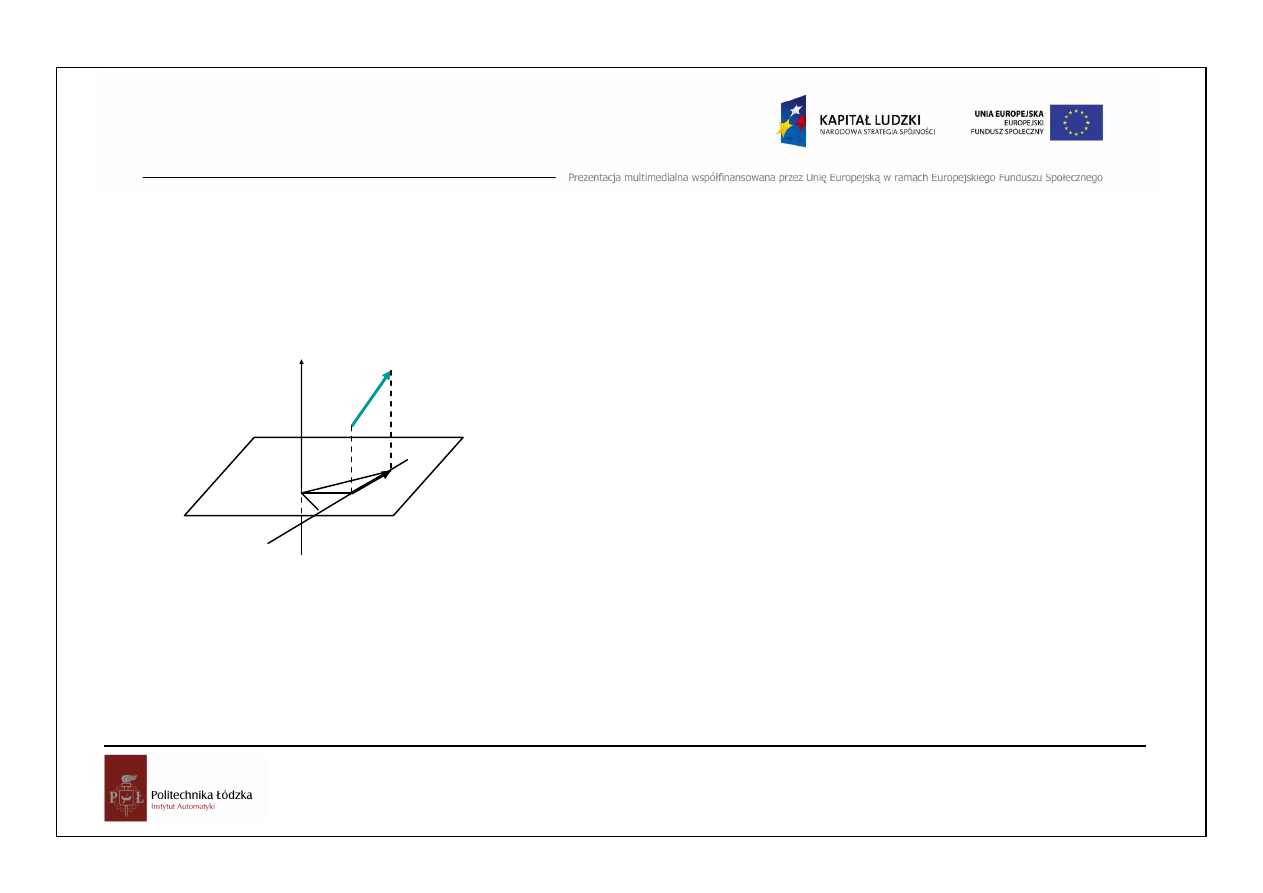
Przykład

Ciało o ciężarze G zawieszone jest na

wsporniku zbudowanym z trzech

prętów.

Znaleść siły w prętach.
Ciężary własne ominąć.
Dane: G,

α,β

x

y

z

α

β

G

7

Mechanika i …

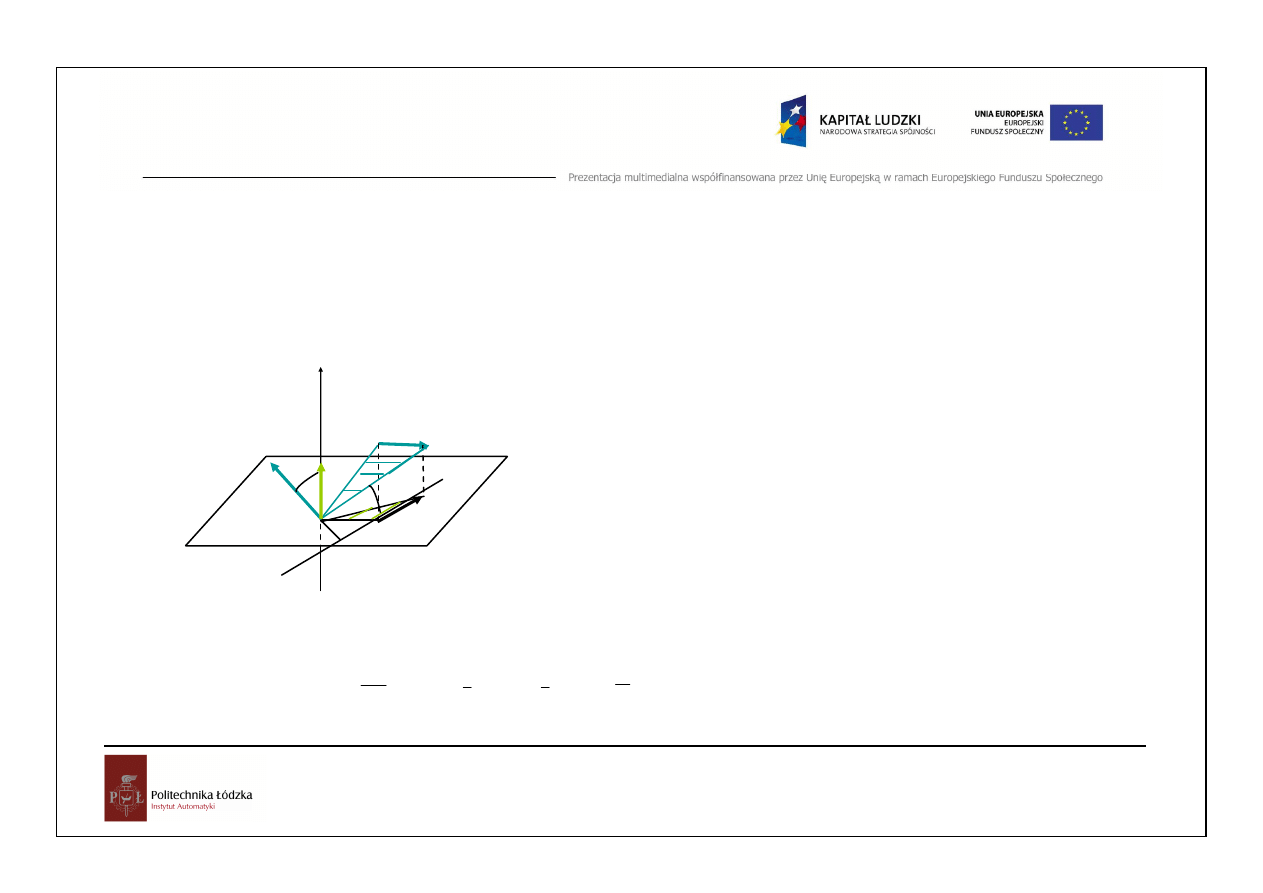
Moment siły wzgl

ę

dem osi

M omentem siły P względem osi z nazywamy moment

rzutu P na p łaszczyznę względem punktu O.

M

P h

P h

F

z

OA B

= ′ ′

′ ′ =

′

2

'

O

P

P’

h’

z

8

Mechanika i …

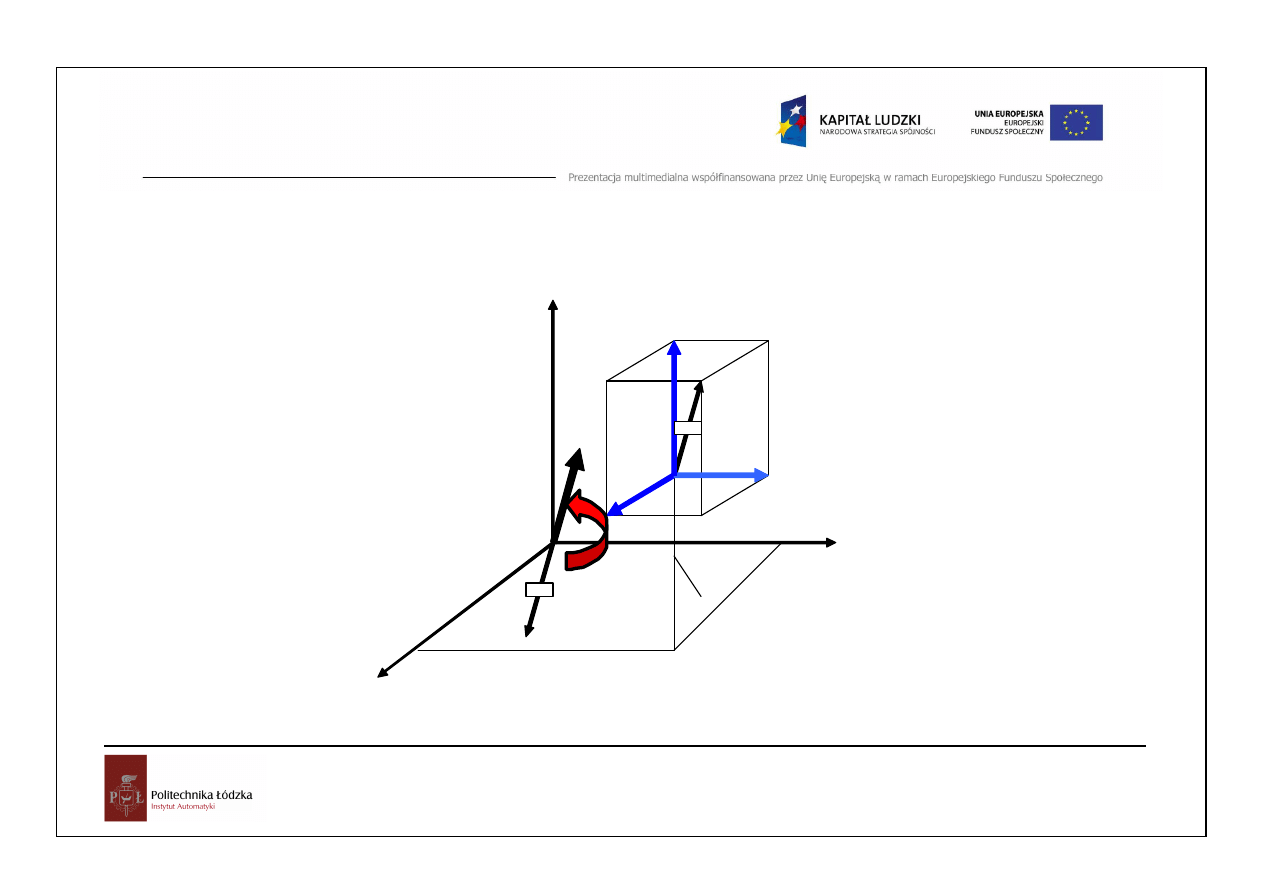
Moment siły wzgl

ę

dem osi

O

P

P’

h’

z

α

α

M oment siły względem osi równa się rzutowi na tę oś
momentu danej siły względem dowolnego punktu leżącego
na tejże osi. Stąd wynika zależność:

M

z

Mo

M

M i

M j

M k

o

x

y

z

=

+

+

9

Mechanika i …

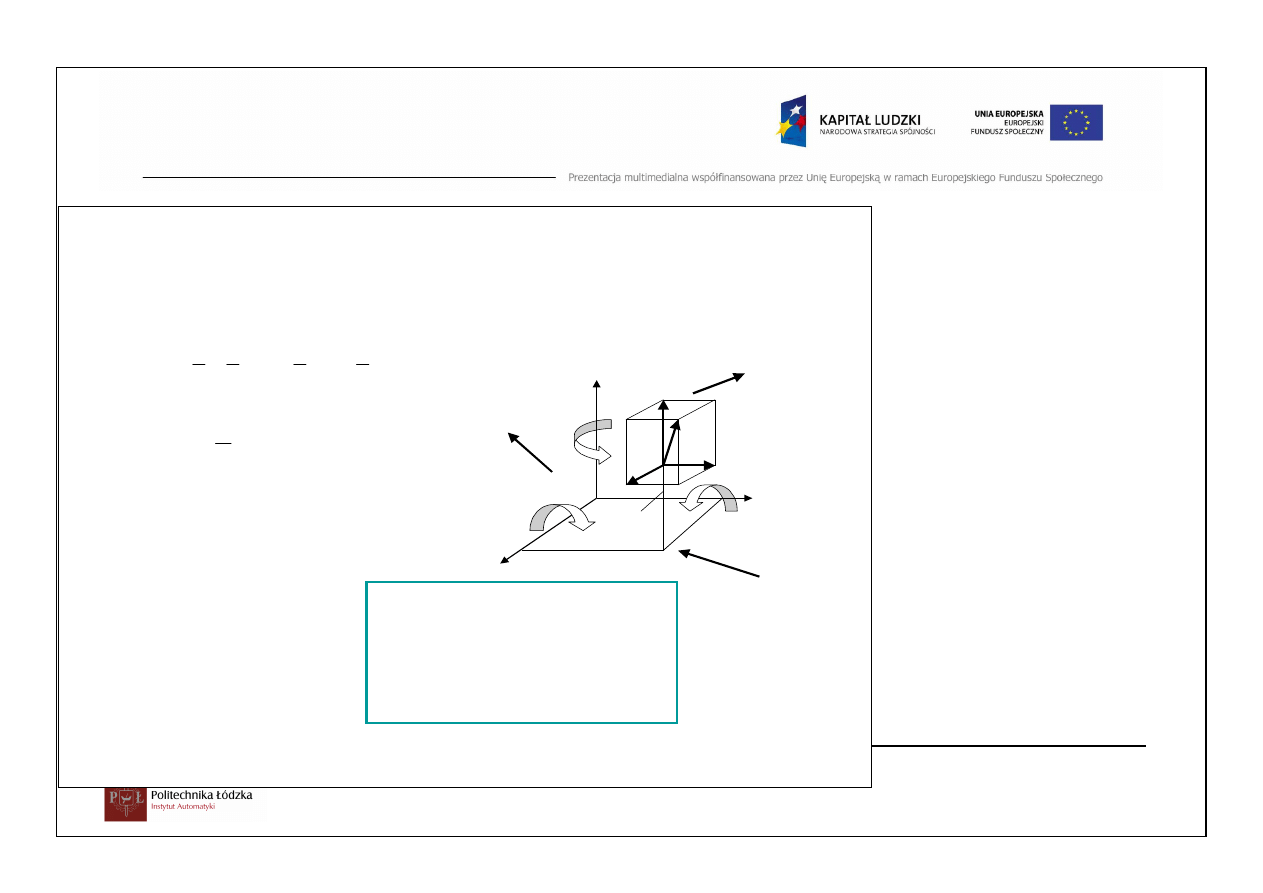
Redukcja wektora głównego R do pocz

ą

tku układu współrz

ę

dnych

R

i

R

ix

R

iz

R

iy

-R

i

M

i

z

x

y

x

i

y

i

z

i

R

i

O

10

Mechanika i …

Dowolny przestrzenny układ sił - warunki

równowagi

0

...

1

2

1

=

=

+

+

+

∑

=

n

i

i

n

P

P

P

P

M

iy

P

i

P

ix

P

iz

P

iy

M

iz

M

ix

z

x

y

x

i

y

i

z

i

P

1

P

2

P

n

∑

=

=

n

i

ix

P

1

0

∑

=

=

n

i

iy

P

1

0

∑

=

=

n

i

iz

P

1

0

(10. 6)

0

1

=

∑

=

n

i

ix

M

0

1

=

∑

=

n

i

iy

M

0

1

=

∑

=

n

i

iz

M

0

1

=

∑

=

n

i

io

M

11

Mechanika i …

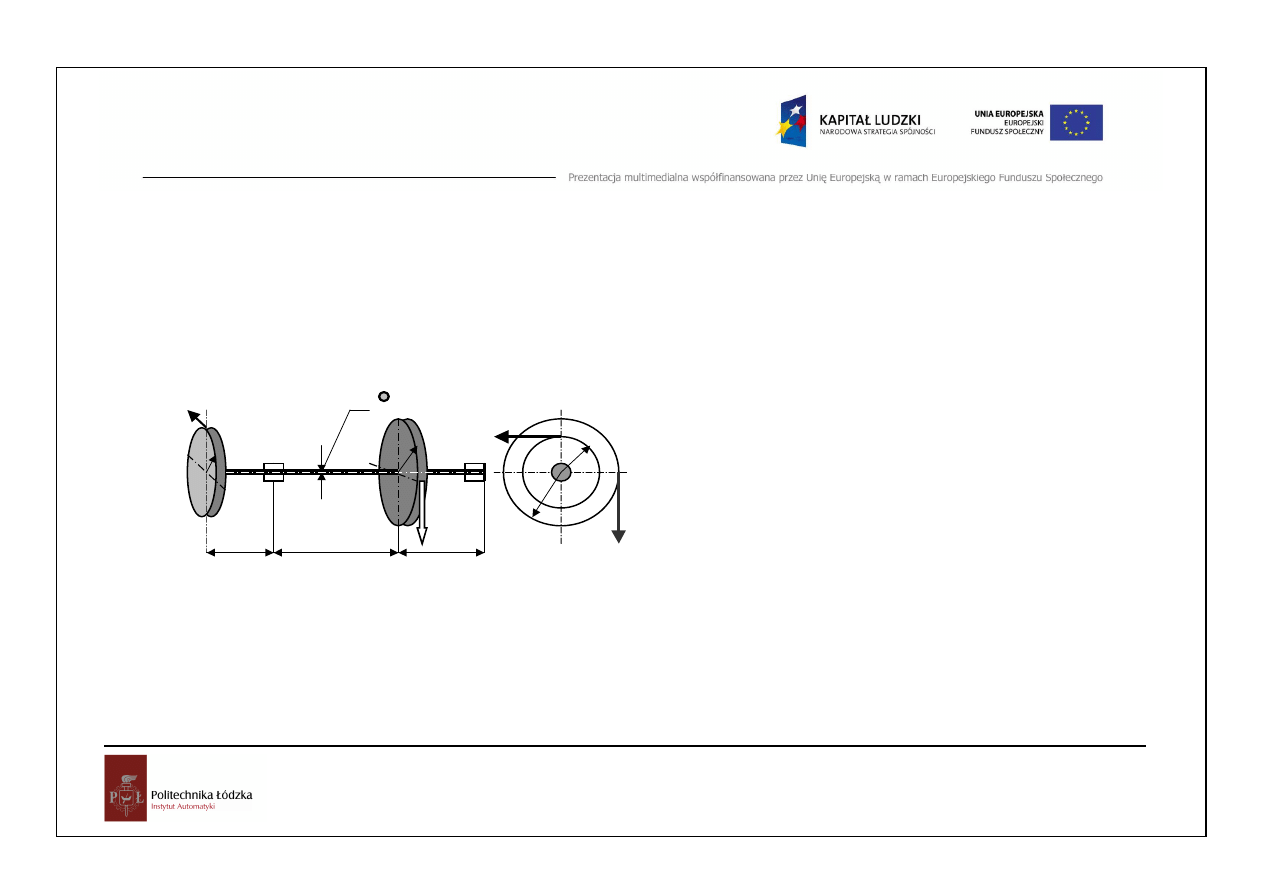
Przykład

2l

P

S

l

2R

A

B

R

l

S

R

P

2R

φ

d

12

Mechanika i …

Wykład 5.

1. Środek sił równoległych

2. Środek ciężkości

3. Metody wyznaczania środków ciężkości

4. Środki ciężkości wybranych linii, figur

płaskich i brył

5. Twierdzenia Pappusa-Guldina

13

Mechanika i …

Przestrzenny układ sił równoległych

Układ sił w przestrzeni, których linie
działania są równoległe nazywamy
układem

sił

równoległych.

Przykładami takich układów sił mogą
być siły

masowe, powierzchniowe,

elektromagnetyczne.

P

1

P

2

P

n

14

Mechanika i …

Ś

rodek sił równoległych

∑

∑

=

=

⋅

=

n

i

i

n

i

i

i

c

P

y

P

y

1

1

A

2

Punk C mający tę własność,
że przechodzi przez niego stale
wypadkowa układu sił równoległych
niezależnie od kierunku tych sił
(przy ich niezmiennych wartościach i
punktach przyłożenia) nazywamy

środkiem sił równoległych

.

P

1

P

2

P

n

A

1

An

C

R

C

1

Współrzędne środka sił równoległych

:

∑

∑

=

=

⋅

=

n

i

i

n

i

i

i

c

P

x

P

x

1

1

∑

∑

=

=

⋅

=

n

i

i

n

i

i

i

c

P

z

P

z

1

1

0

1

=

∑

=

n

i

ix

M

0

1

=

∑

=

n

i

iy

M

0

1

=

∑

=

n

i

iz

M

15

Mechanika i …

Ś

rodek ci

ęż

ko

ś

ci

iy

∆

G

1

∆

G

2

∆

G

i

∆

G

n

iz

z

x

y

x

i

y

i

z

i

∆

G

3

G

Ciężar możemy przedstawić jako iloczyn ciężaru właściwego

γγγγ

i

pomnożonego przez objętość -

∆

Gi=

∆∆∆∆

Vi

⋅γ

⋅γ

⋅γ

⋅γ

i (lub masę jako iloczyn

masy

właści wej

i

obję tości)

zatem

po

uproszczeniu

otrzymujemy:

V

x

V

x

n

i

i

i

i

c

∑

=

⋅

∆

=

1

γ

V

y

V

y

n

i

i

i

i

c

∑

=

⋅

∆

=

1

γ

V

z

V

z

n

i

i

i

i

c

∑

=

⋅

∆

=

1

γ

16

Mechanika i …

Współrz

ę

dne

ś

rodka ci

ęż

ko

ś

ci

V

x

V

x

i

n

i

i

i

i

c

γ

γ

∑

=

⋅

∆

=

1

V

y

V

y

i

n

i

i

i

i

c

γ

γ

∑

=

⋅

∆

=

1

V

z

V

z

i

n

i

i

i

i

c

γ

γ

∑

=

⋅

∆

=

1

Przechodząc do granicy przy

∆

Vi → 0

oraz zakładając

γ

i

= const.

otrzymujemy

:

V

xdV

x

V

c

∫

=

V

ydV

y

V

c

∫

=

V

zdV

z

V

c

∫

=

17

Mechanika i …

Współrz

ę

dne

ś

rodka ci

ęż

ko

ś

ci

V

xdV

x

V

c

∫

=

V

ydV

y

V

c

∫

=

V

zdV

z

V

c

∫

=

Bryły:

Analogicznie, figury płaskiej:

F

xdF

x

F

c

∫

=

F

ydF

y

F

c

∫

=

Linii:

l

xdl

x

l

c

∫

=

l

ydl

y

l

c

∫

=

l

zdl

z

l

c

∫

=

18

Mechanika i …

Metody wyznaczania

ś

rodków ci

ęż

ko

ś

ci

•Jeżeli ciało materialne posiada płaszczyznę , oś lub środek symetrii, to środek
ciężkości leży
odpowiednio w tej płaszczyźnie, na tej osi lub pokrywa się ze środkiem symetrii.

• Ciało materialne możemy podzielić myślowo na części, dla których położenia
ś

rodków ciężkości są znane , następnie zastosować następujące wzory:

- dla bryły

- dla figury płaskiej

- dla linii

V

x

V

x

n

i

i

i

c

∑

=

⋅

=

1

V

y

V

y

n

i

i

i

c

∑

=

⋅

=

1

V

z

V

z

n

i

i

i

c

∑

=

⋅

=

1

∑

∑

=

=

⋅

=

n

i

i

n

i

i

i

c

F

x

F

x

1

1

∑

∑

=

=

⋅

=

n

i

i

n

i

i

i

c

F

y

F

y

1

1

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

⋅

=

⋅

=

⋅

=

n

i

i

n

i

i

i

c

n

i

i

n

i

i

i

c

n

i

i

n

i

i

i

c

L

z

L

z

L

y

L

y

L

x

L

x

1

1

1

1

1

1

;

;

19

Mechanika i …

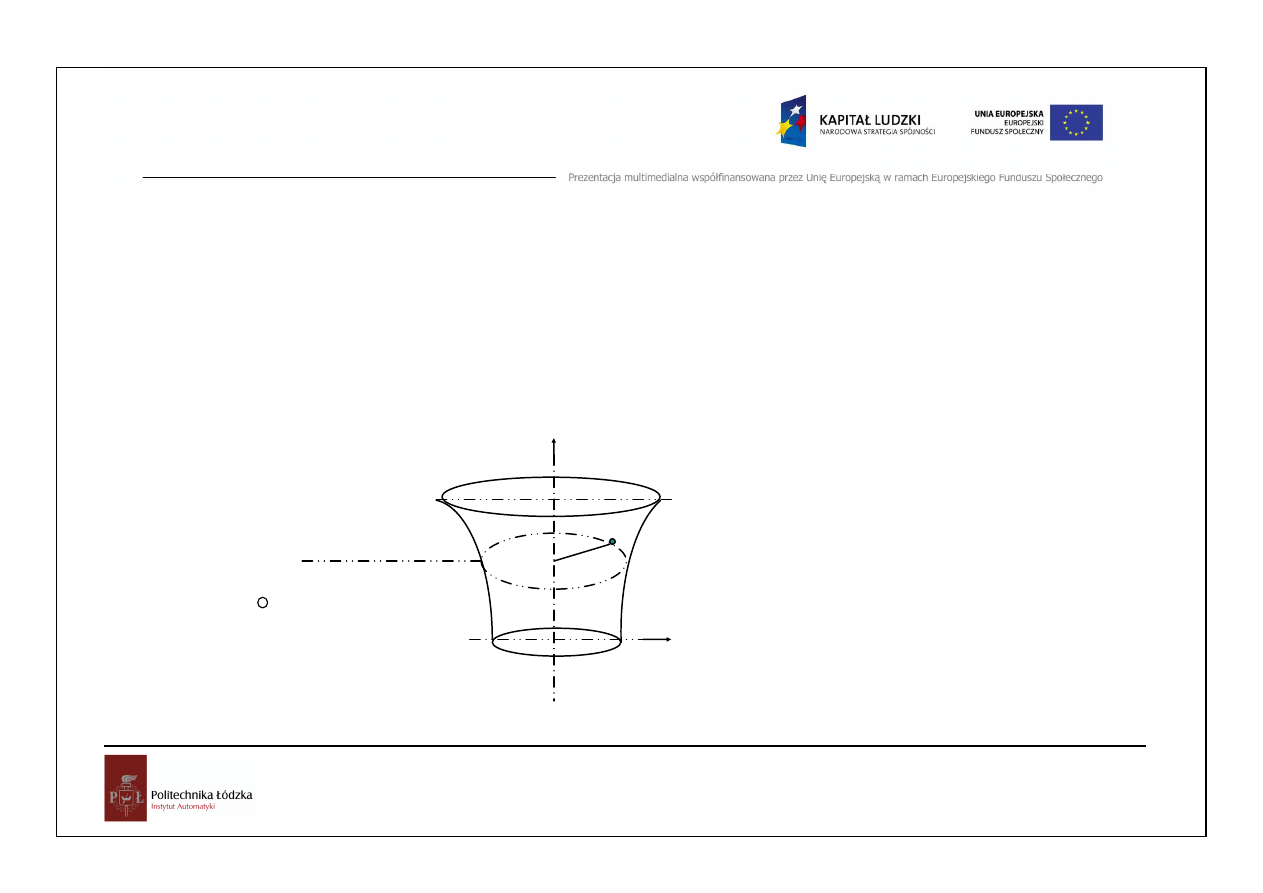
Twierdzenia Pappusa-Guldina

x

c

C

x

I.

Twierdzenie: Pole powierzchni obrotowej, powstałe wskutek

obrotu płaskiej linii wokół osi leżącej w jej płaszczyźnie równe jest

długości tej linii pomnożonej przez długość okręgu, który opisuje jej środek ciężkości

y

A

B

AB

c

l

x

xdl

F

⋅

⋅

=

=

∫

π

π

2

2

20

Mechanika i …

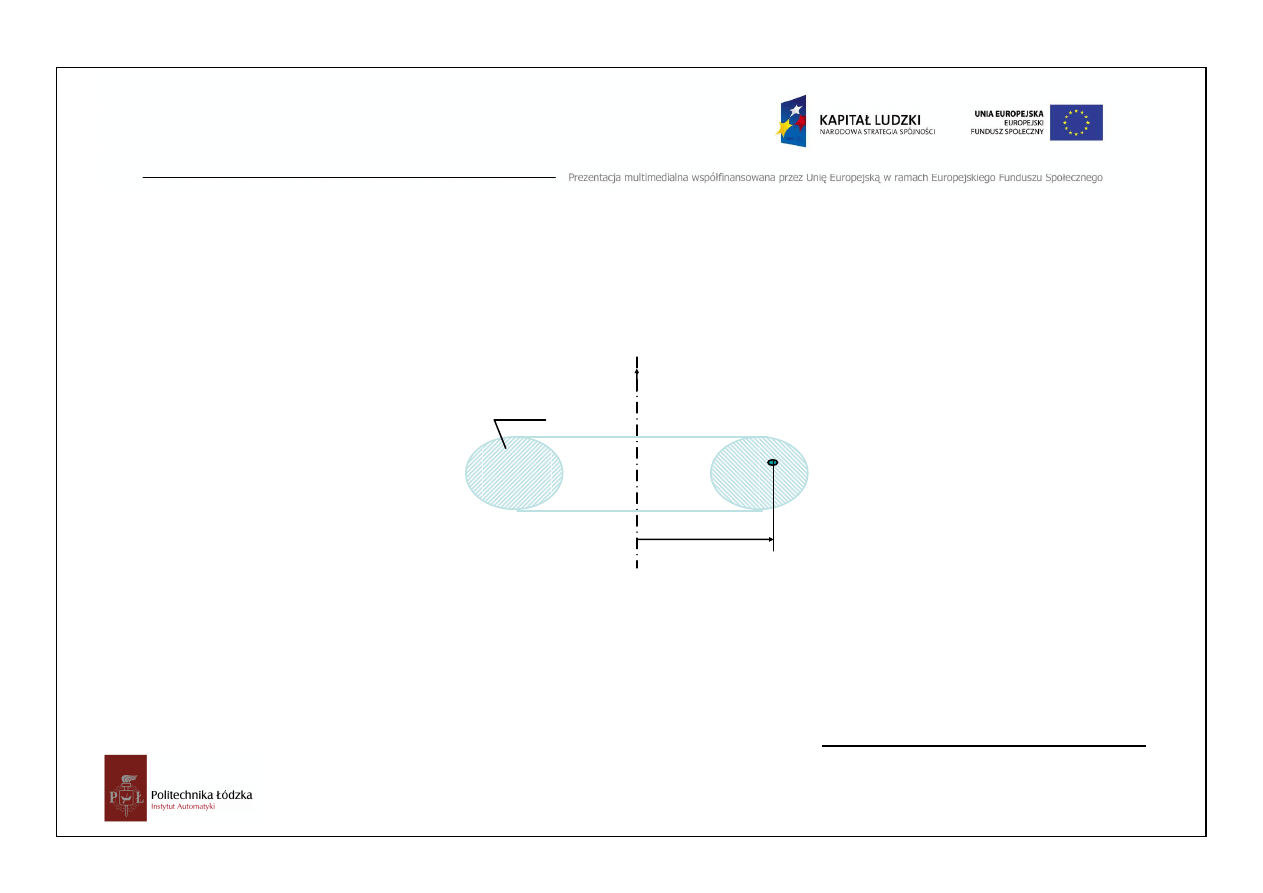
Twierdzenia Pappusa-Guldina

C

x

c

II.

Twierdzenie: Objętość bryły obrotowej,

powstałej wskutek obrotu figury
płaskiej wokół osi leżącej w jej
płaszczyźnie

i nie przecinającej tej figury, równa jest
polu powierzchni tej figury pomnożonemu

przez długość okręgu, który opisuje jej
ś

rodek ciężkości.

F

x

xdF

V

c

F

⋅

⋅

=

=

∫

π

π

2

2

F