Maria Kotełko

Mechanika

i Wytrzymało

ść

Materiałów

————————————————————————————————————————

Zadanie nr 32 - Dostosowanie kierunku Automatyka i Robotyka

do prowadzenia studiów niestacjonarnych

2

Mechanika i …

Cz

ęść

I - Mechanika

Wykład 3.

1. Płaski układ sił zbie

ż

nych

2. Twierdzenie o trzech siłach

3. Moment siły wzgl

ę

dem punktu

4. Wypadkowa sił równoległych i anty-równoległych. Para sił.

5. Dowolny płaski układ sił

6. Redukcja dowolnego płaskiego układu sił

7. Warunki równowagi dowolnego płaskiego

układu sił

3

Mechanika i …

Warunek równowagi płaskiego układu sił

zbie

ż

nych

P

P

P

P

n

i

i

n

1

2

1

0

+ + + =

=

=

∑

...

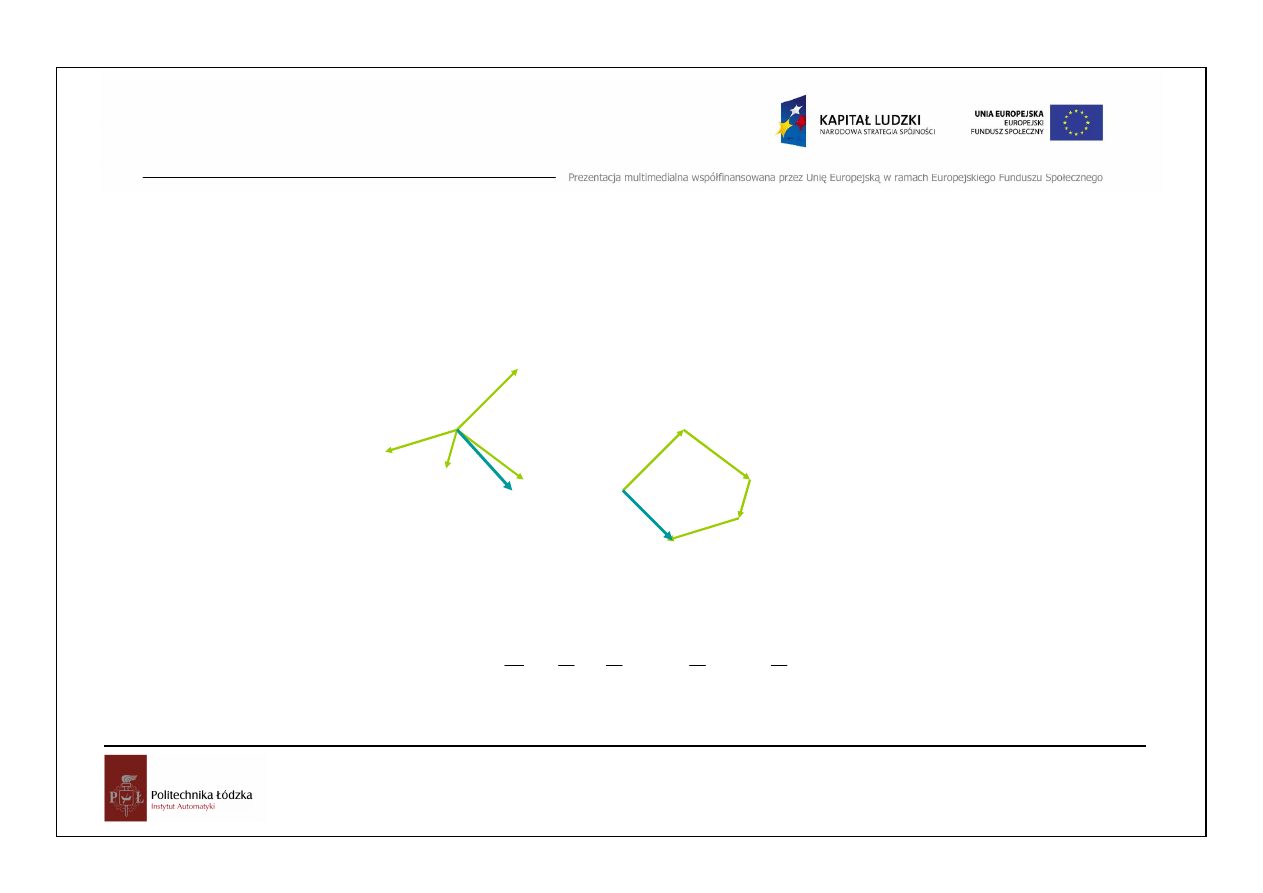
Warunkiem równowagi płaskiego układu sił zbie

ż

nych jest, aby ich

wypadkowa była równa zeru.

Ab y siły zbie

ż

ne P

1

, P

2

, ... działaj

ą

ce w jednej płaszczy

ż

nie, był y

w równowadze, wielobok z nich zbudowany (wielobok sił) musi by

ć

wielobokiem zamkni

ę

tym

.

4

Mechanika i …

Płaski układ sił zbie

ż

nych

Płaskim

układem

sił

zbie

ż

nych

nazywamy układ sił na płaszczy

ź

nie,

których linie działania przecinaj

ą

si

ę

w jednym punkcie.

P

1

Dowolny płaski układ sił zbie

ż

nych przyło

ż

onych w punkcie

O mo

ż

emy zast

ą

pi

ć

sił

ą

wypadkow

ą

R równ

ą

sumie

geometrycznej ( wektorowej ) tych sił i przyło

ż

on

ą

równie

ż

w punkcie O.
Wypadkowa R „zamyka” wielobok sił.

P

2

P

n

R

O

R

P

P

P

P

n

i

i

n

= + + + =

=

∑

1

2

1

...

5

Mechanika i …

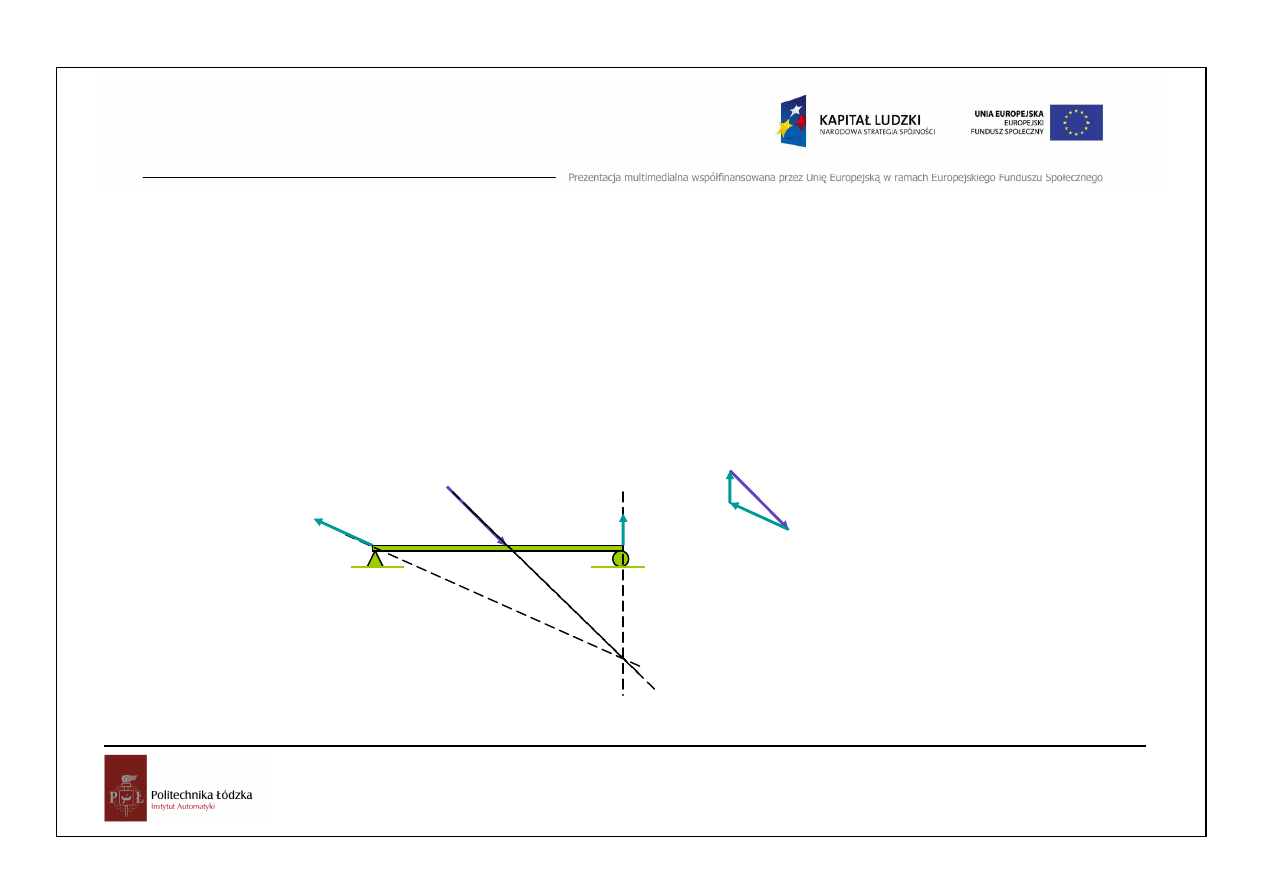
Twierdzenie o trzech siłach

Ab y trzy siły nierównoległe

działaj

ą

ce

na

ciało

sztywne

był y w

równowadze, linie działania tych sił musz

ą

przecina

ć

si

ę

w jednym

punkcie, a same siły musz

ą

tworzy

ć

trójk

ą

t zamkni

ę

ty.

P

R

1

R

2

6

Mechanika i …

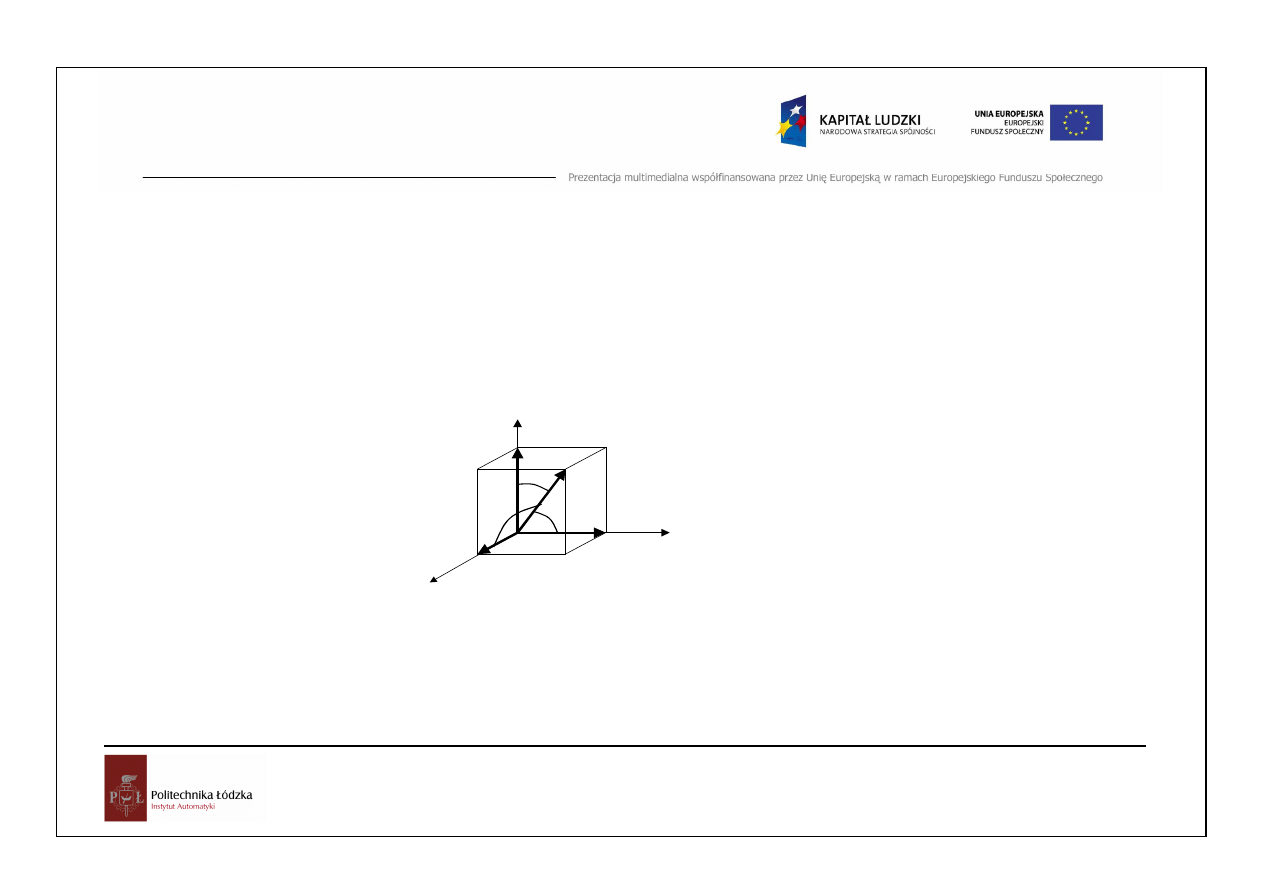
Zasady rzutowania w przestrzeni

P

i

P

ix

P

iz

P

iy

z

x

y

α

αα

α

i

ββββ

i

γγγγ

i

i

i

ix

P

P

α

cos

⋅

=

,

i

i

iy

P

P

β

cos

⋅

=

,

i

i

iz

P

P

γ

cos

⋅

=

7

Mechanika i …

Równania równowagi płaskiego układu sił zbie

ż

nych

wyra

ż

one w ich składowych:

Aby siły zbie

ż

ne le

żą

ce w jednej płaszczy

ż

nie były w równowadze, sumy rzutów tych sił na osie

układu współrz

ę

dnych musz

ą

by

ć

równe zeru.

0

0

1

1

=

=

∑

∑

=

=

n

i

iy

n

i

ix

P

P

8

Mechanika i …

Moment siły wzgl

ę

dem punktu

Moment siły P wzgl

ę

dem punktu O jest iloczynem wektorowym promienia wektora r oraz siły

P.

.

O

P

M=



P



r sin

α

h=r

⋅

sin

α

α

M=

r

××××

P

r

A

B

z

y

x

z

y

x

P

P

P

r

r

r

k

j

i

P

r

M

r

r

r

r

r

r

=

×

=

9

Mechanika i …

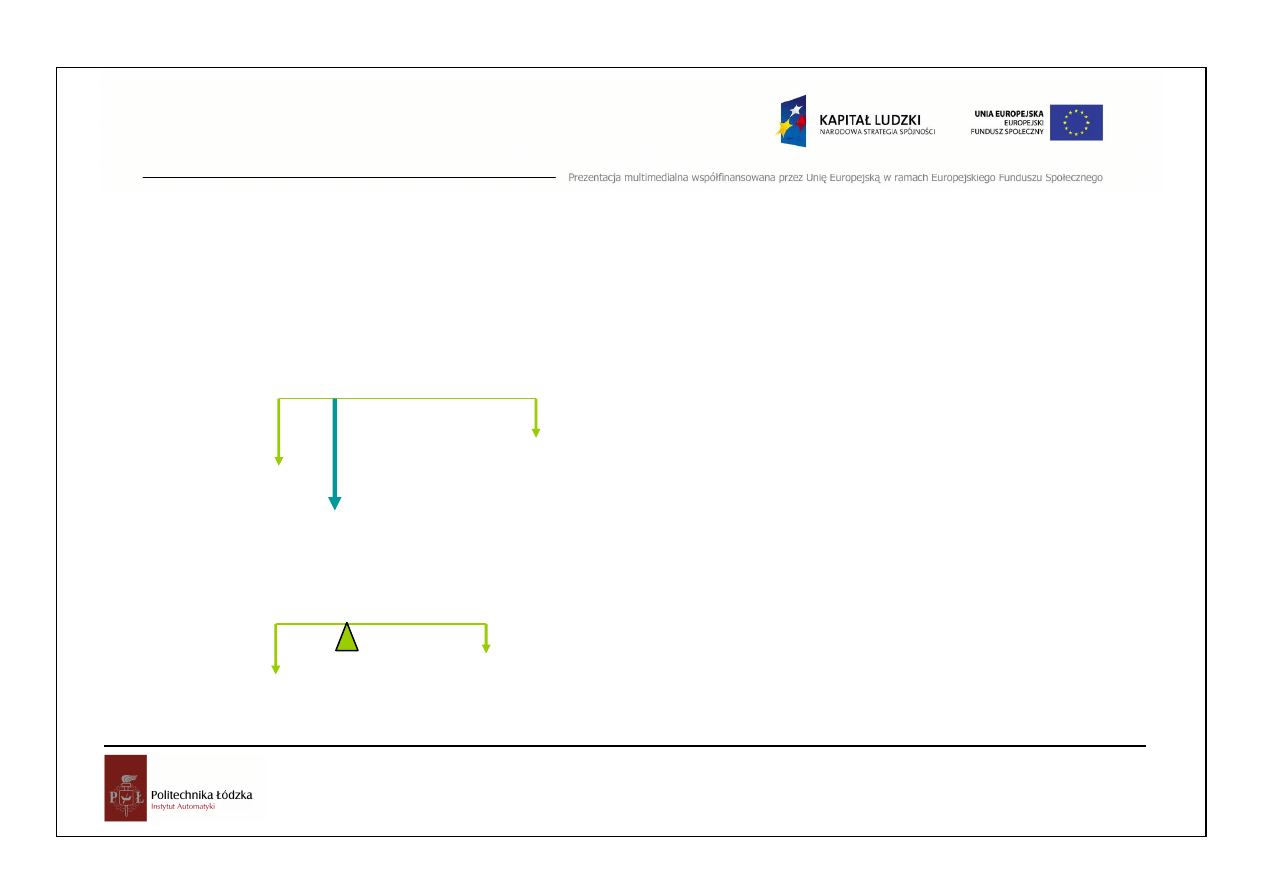
Wypadkowa sił równoległych

P

1

P

2

R

r

1

r

2

2

2

1

1

2

1

r

P

r

P

P

P

R

=

+

=

P

1

P

2

r

1

r

2

2

2

1

1

r

P

r

P

=

Praw o d

ź

wigni:

10

Mechanika i …

Wypadkowa sił anty-równoległych

P

1

P

2

R

r

1

r

2

2

2

1

1

2

1

r

P

r

P

P

P

R

=

−

=

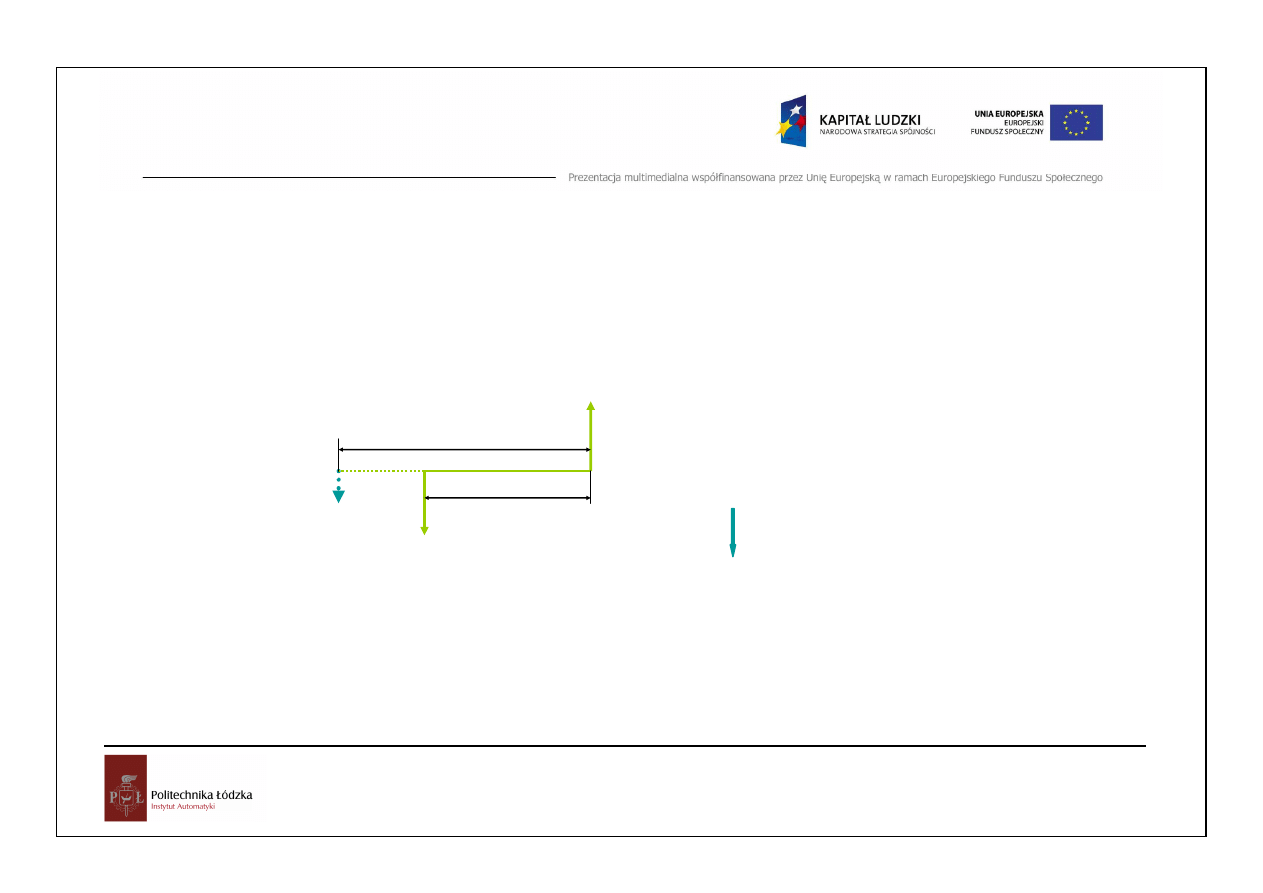
11

Mechanika i …

Para sił – szczególny przypadek sił anty-

równoległych

1

1

2

2

1

;

;

0

a

r

r

r

P

r

P

P

P

R

+

=

=

=

−

=

P

P

R=0

r

1

r

2

a

→∝

1

r

Wypadkowa pary sił nie istnieje!

Moment pary sił M=Pa

Moment pary sił nie zale

ż

y od punktu, wzgl

ę

dem którego

obliczamy momenty obu sił.

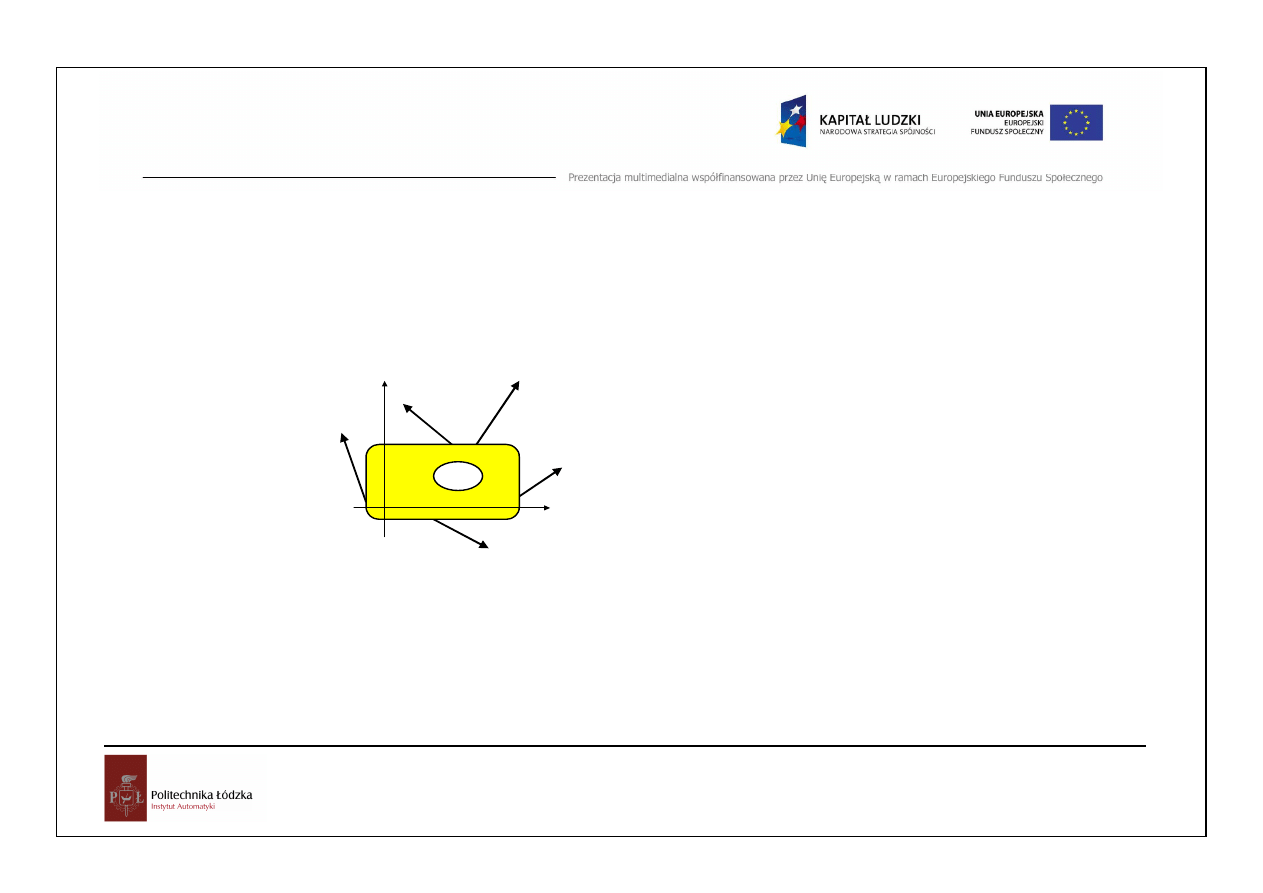
12

Mechanika i …

Dowolny płaski układ sił

x

y

P

1

P

2

P

3

P

i

P

n

O

∑

=

i

i

P

R

r

r

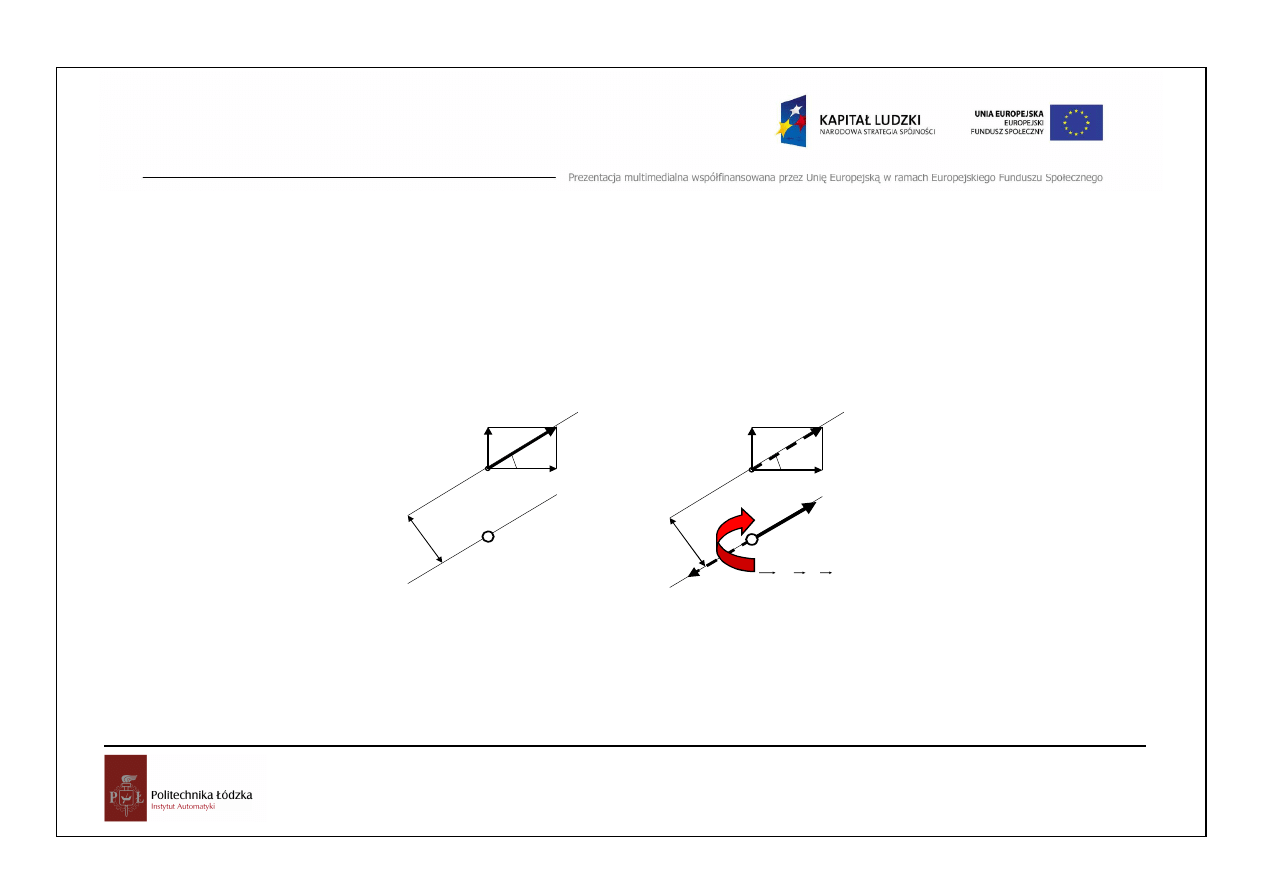
13

Mechanika i …

Redukcja siły P

i

do dowolnego punktu O

h

i

O

P

i

P

ix

= P

i

cos

α

i

P

iy

=P

i

sin

α

i

α

i

h

i

O

P

i

P

i

P

ix

= P

i

cos

α

i

P

iy

=P

i

sin

α

i

α

i

i

i

P

h

M

×

=

-P

i

Prze suwaj

ą

c równolegle wektor P

i

do punktu O przykładamy do tego punktu

zerowy u kład sił (

±

Pi), wówcza s siły oznaczone liniami przerywanymi tworz

ą

moment pary sił

M

i

=P

i

⋅

h

i

wzgl

ę

dem punktu O. Działanie to mo

ż

emy powtórzy

ć

dla ka

ż

dej siły Pi działaj

ą

cej na ciało sztywne

.

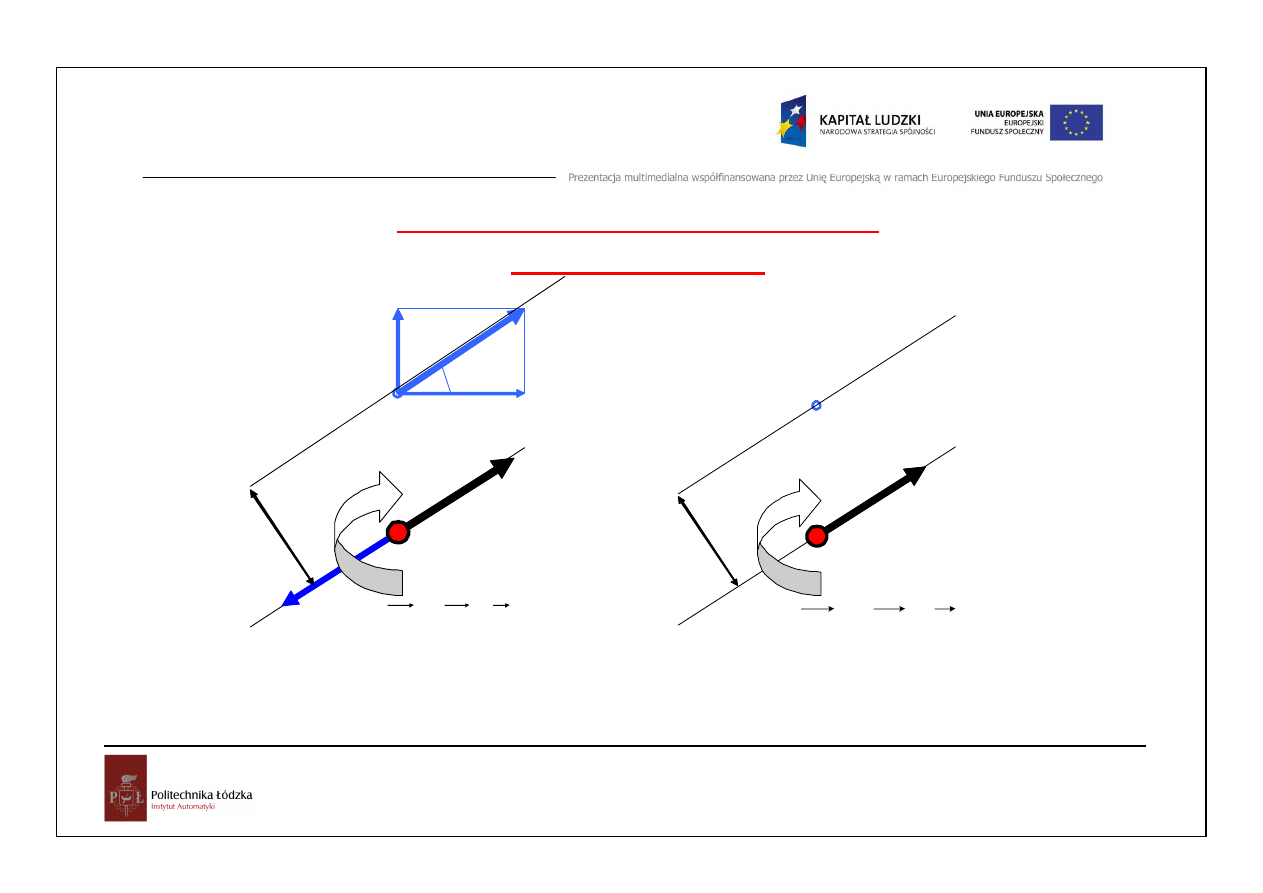
14

Mechanika i …

Redukcja układu sił do wektora głównego

i momentu głównego

∑

=

=

n

i

iA

M

M

1

v

r

h

R

O

R

R

R

x

= Rcos

α

R

y

=Rsin

α

α

R

h

M

R

×

=

R

A

h

R

O

R

R

h

M

R

×

=

A

15

Mechanika i …

Warunki równowagi dowolnego płaskiego układu

sił

x

y

P

1

P

2

P

3

P

i

P

n

O

0

=

=

∑

i

i

P

R

r

r

0

1

=

=

∑

=

n

i

iA

M

M

v

r

∑

=

=

n

i

ix

P

1

0

∑

=

=

n

i

iy

P

1

0

0

1

=

∑

=

n

i

iA

M

Warun ki równowagi w postaci skalarnej:

Aby dowolny płaski układ sił
znajdował si

ę

w równowadze

zarówno wektor główny R jak i
moment główny M musz

ą

by

ć

równe zeru.