Maria Kotełko
Mechanika
i Wytrzymało
ść
Materiałów
————————————————————————————————————————
Zadanie nr 32 - Dostosowanie kierunku Automatyka i Robotyka
do prowadzenia studiów niestacjonarnych
Maria Kotełko
Mechanika
i Wytrzymało
ść
Materiałów
————————————————————————————————————————
Zadanie nr 32 - Dostosowanie kierunku Automatyka i Robotyka
do prowadzenia studiów niestacjonarnych
2
Mechanika i …
Przedmiot: Mechanika i Wytrzymało
ść
Materiałów
Wykładowca: dr hab. in
Ŝ
. Maria Kotełko, prof.PŁ
Katedra Wytrzymało
ś
ci Materiałów i Konstrukcji PŁ
Maria.Kotelko@p.lodz.pl mechmat@p.lodz.pl
Zalecana literatura:
1. Jaroniek M.: Podstawy Mechaniki Technicznej dla Studentów Wydziału Elektroniki i Elektrotechniki - Skrypt
- Wyd. Politechniki Łódzkiej, Łód
ź
2004
2. Leyko J.: Mechanika Ogólna, PWN, Warszawa 1970, Tom 1. - Statyka i Kinematyka
3. Niezgodzi
ń
ski M.E. Niezgodzi
ń
ski T.: Wytrzymało
ść
Materiałów, wyd. XIV PWN, Warszawa 1998
4. Niezgodzi
ń
ski M. Niezgodzi
ń
ski T. Walczak W.: Mechanika Ogólna w Zadaniach, cz. 1 - Statyka, Politechnika
Łódzka, Łód
ź
1994
5. Banasiak M. Grossman K. Trombski M.: Zbiór zada
ń
z Wytrzymało
ś
ci Materiałów, PWN, Warszawa 1992
(*) w niniejszym opracowaniu wykorzystano fragmenty tej publikacji za zgod
ą
Autora
3
Mechanika i …
Cz
ęść
I - Mechanika
Wykład 1.
1. Poj
ę
cia podstawowe
2. Podstawy mechaniki klasycznej – prawa Newtona
3. Zasady statyki ciała sztywnego
4. Wi
ę
zy i ich reakcje
5. Podstawy algebry wektorów
4
Mechanika i …
Mechanika jest cz
ęś
ci
ą
fizyki zajmuj
ą
c
ą
si
ę
zjawiskami ruchu i równowagi.
Definicja Newtona:
Racjonalna mechanika jest nauk
ą
o ruchach odbywaj
ą
cych si
ę
pod działaniem jakichkolwiek sił i o siłach potrzebnych do
spowodowania odpowiednich ruchów.
Mechanika
statyka kinematyka dynamika
nauka o układach nauka o geometrii ruchu nauka zajmuj
ą
ca si
ę
materialnych w równowadze zale
Ŝ
no
ś
ciami pomi
ę
dzy ruchem ciał
a siłami na nie działaj
ą
cymi
statyka ciała sztywnego statyka ciał odkształcalnych
(wytrzymało
ść
materiałów)
5
Mechanika i …
Poj
ę
cia podstawowe:
Czas
- porz
ą
dkuje kolejno
ść
zdarze
ń
,
Długo
ść
- poj
ę
cie opisuj
ą
ce wielko
ść
(wymiar) przedmiotu – musi istnie
ć
wzorzec, z którym
porównujemy ten wymiar,
Masa
– pewna własno
ść
materii b
ę
d
ą
ca miar
ą
bezwładno
ś
ci,
Siła
– oddziaływanie jednego ciała na drugie, powoduj
ą
ce zmian
ę
ruchu ciała,
Punkt materialny
– punkt w sensie geometrycznym o niesko
ń
czenie małych wymiarach i
okre
ś
lonej masie,
Continuum materialne –
o
ś
rodek ci
ą
gły, zbiór punktów materialnych o masie rozło
Ŝ
onej w
sposób ci
ą
gły,
Ciało idealnie sztywne –
odległo
ść
dwu dowolnych punktów w obr
ę
bie tego ciała pozostaje
stała (ciało to nie ulega odkształceniu).
6
Mechanika i …
Wielko
ś
ci fizyczne
Zasadnicze Pochodne
Musz
ą
by
ć
3 ………………
w ukł. SI: długo
ść
(metr),
siła (niuton)
czas (sekunda)
Wektory Skalary
Wielkości, które przy znanej jednostce są określone przez jedną liczbę
nazywamy skalarami (np. długość, masa, gęstość, temperatura, energia).
Wielkości definiowane przez kierunek (linię działania),
wartość bezwzględną (moduł) oraz zwrot (np. siła, przyspieszenie, prędkość).
7
Mechanika i …
Mechanika klasyczna oparta jest na trzech prawach dynamiki Newtona ( Izaak Newton - 1687). W odniesieniu do punktu
materialnego brzmi
ą
one:
Prawo I.
Punkt materialny na który nie działa
Ŝ
adna siła pozostaje w spoczynku lub porusza si
ę
ruchem jednostajnym po linii
prostej.
Prawo II.
Przyspieszenie punktu materialnego jest proporcjonalne do siły działaj
ą
cej na ten punkt i ma kierunek siły.
m p
P
⋅ =
m - masa punktu materialnego
Prawo III.
Siły wzajemnego oddziaływania dwu punktów materialnych s
ą
równe co do warto
ś
ci i przeciwnie skierowane wzdłu
Ŝ
prostej ł
ą
cz
ą
cej oba punkty.
1
,
2
2
,
1
1
,
2
2
,
1
P
P
P
P
=
−
=
8
Mechanika i …
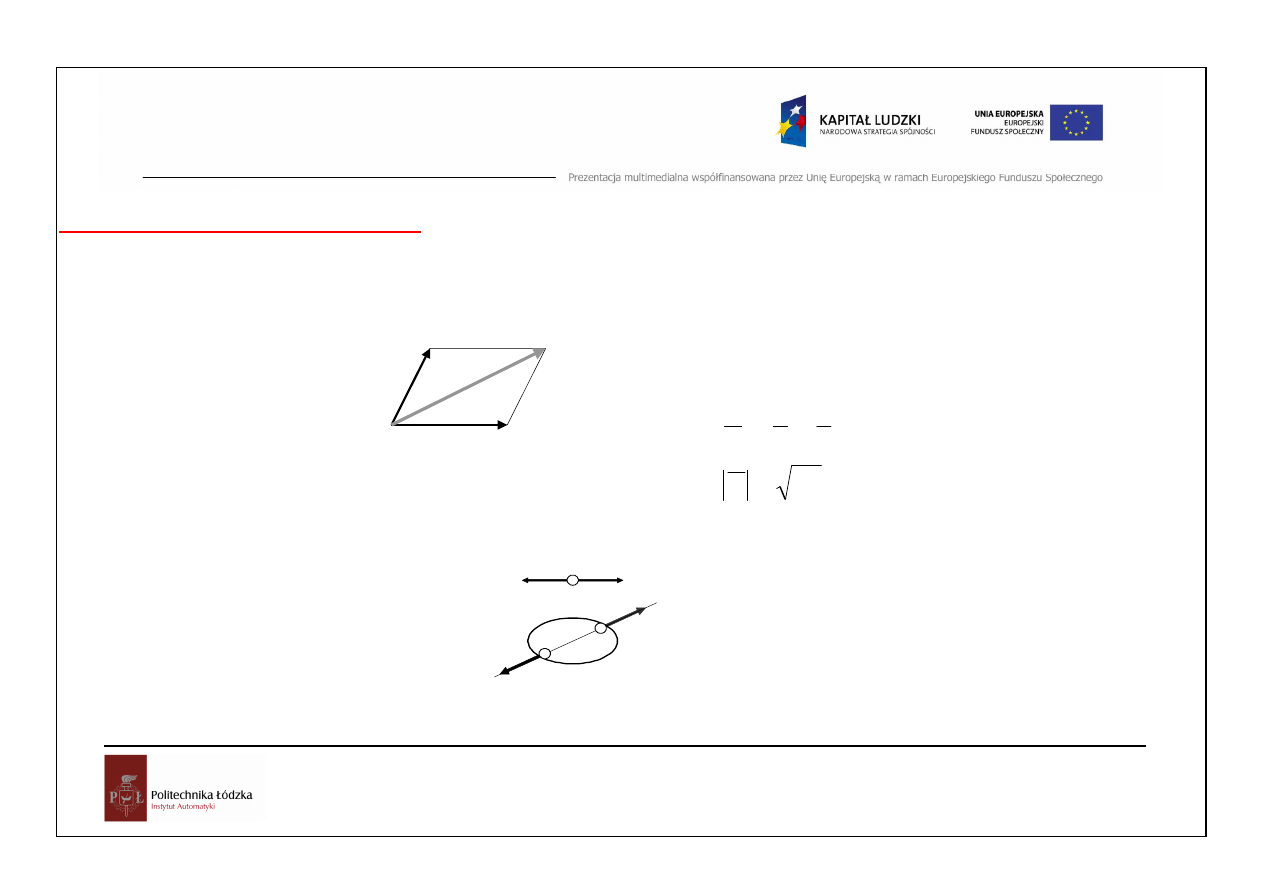
Zasady statyki ciała sztywnego:
I. Zasada równoległoboku
Wypadkowa dowolnych sił P
1
, P
2
przyło
Ŝ
onych do jednego punktu jest wektorem b
ę
d
ą
cym przek
ą
tn
ą
równoległoboku zbudowanego na wektorach tych sił.
P
2
P
1
R
α
β
β
α
ϕ
+
=
R
P
P
R
P
P
P P
= +
=
+
+
1
2
1
2
2
2
1 2
2
cos
φ
II. Zasada
Dwie siły przyło
Ŝ
one do ciała sztywnego równowa
Ŝą
si
ę
tylko wtedy, gdy działaj
ą
wzdłu
Ŝ
jednej prostej, s
ą
przeciwnie
skierowanei i maj
ą
te same warto
ś
ci liczbowe.
-S
S
P
-P
Taki układ sił nazywamy układem zerowym.
9
Mechanika i …
III. Zasada
Działanie układu sił przyło
Ŝ
onych do ciała sztywnego nie ulegnie zmianie, je
Ŝ
eli do układu tego dodamy lub od niego
odejmiemy układ sił równowa
Ŝą
cych si
ę
, to jest tzw. układ zerowy.
Oznacza to,
Ŝ
e wektor siły przyło
Ŝ
onej do ciała sztywnego jest wektorem swobodnym.
-S
S
S
+S
S
IV. Zasada zesztywnienia
Równowaga sił działaj
ą
cych na ciało odkształcalne nie zostanie naruszona przez zesztywnienie tego ciała.
V. Zasada
Ka
Ŝ
demu działaniu towarzyszy równe co do warto
ś
ci i przeciwnie skierowane wzdłu
Ŝ
tej samej prostej
przeciwdziałanie.
To jest III. Prawo Newtona w odniesieniu do ciała sztywnego.
10
Mechanika i …
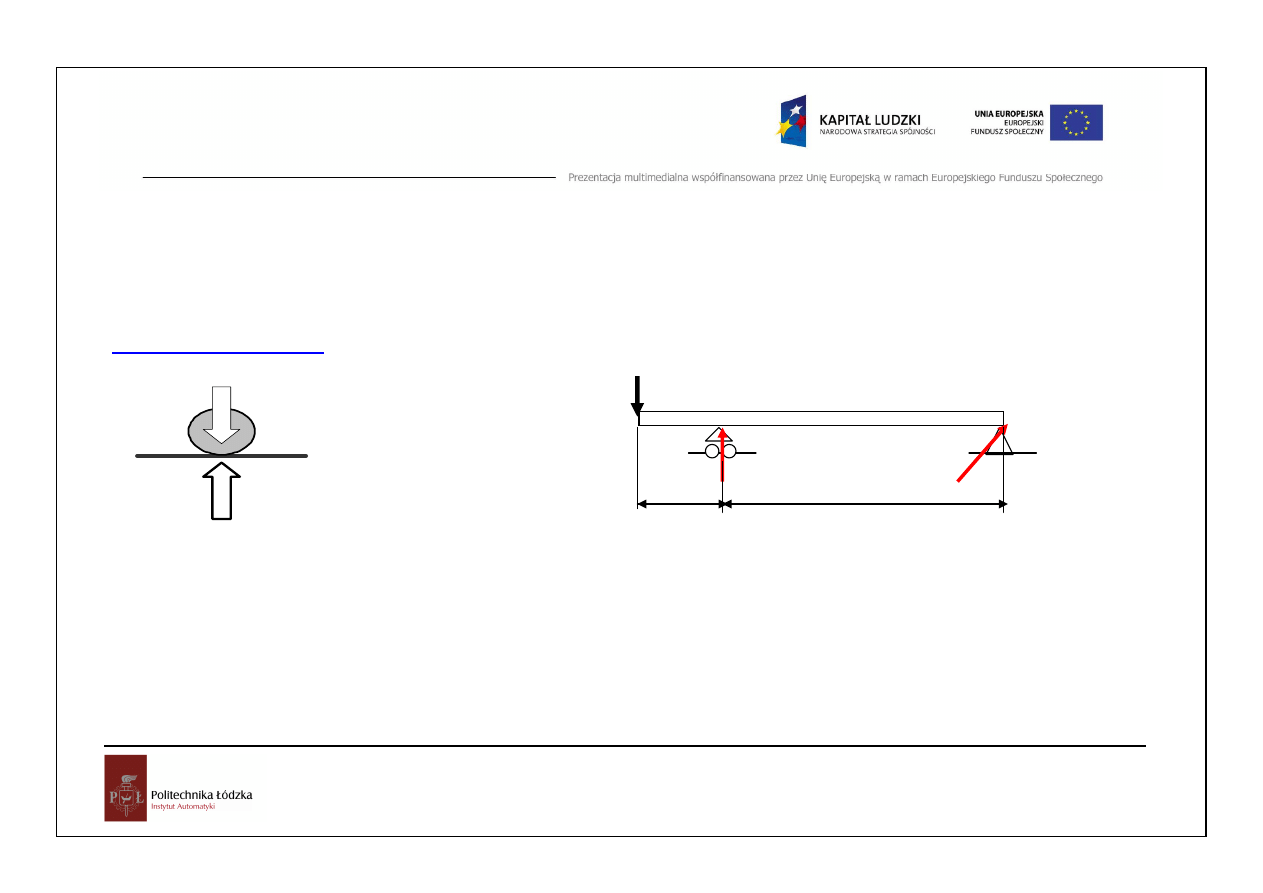
VI. Zasada
oswobodzenia od wi
ę
zów
Ka
Ŝ
de ciało nieswobodne mo
Ŝ
na my
ś
lowo oswobodzi
ć
od wi
ę
zów, zast
ę
puj
ą
c ich działanie odpowiednimi reakcjami.
Dalej mo
Ŝ
na rozpatrywa
ć
ciało jako swobodne - podlegaj
ą
ce działaniu sił czynnych i reakcji wi
ę
zów.
Wi
ę
zy i ich reakcje
.
G
R
Reakcje podło
Ŝ
a Podpory: przesuwna stała
11
Mechanika i …
Dźwigar mostu
Podpora stała
Podpora przesuwna
12
Mechanika i …
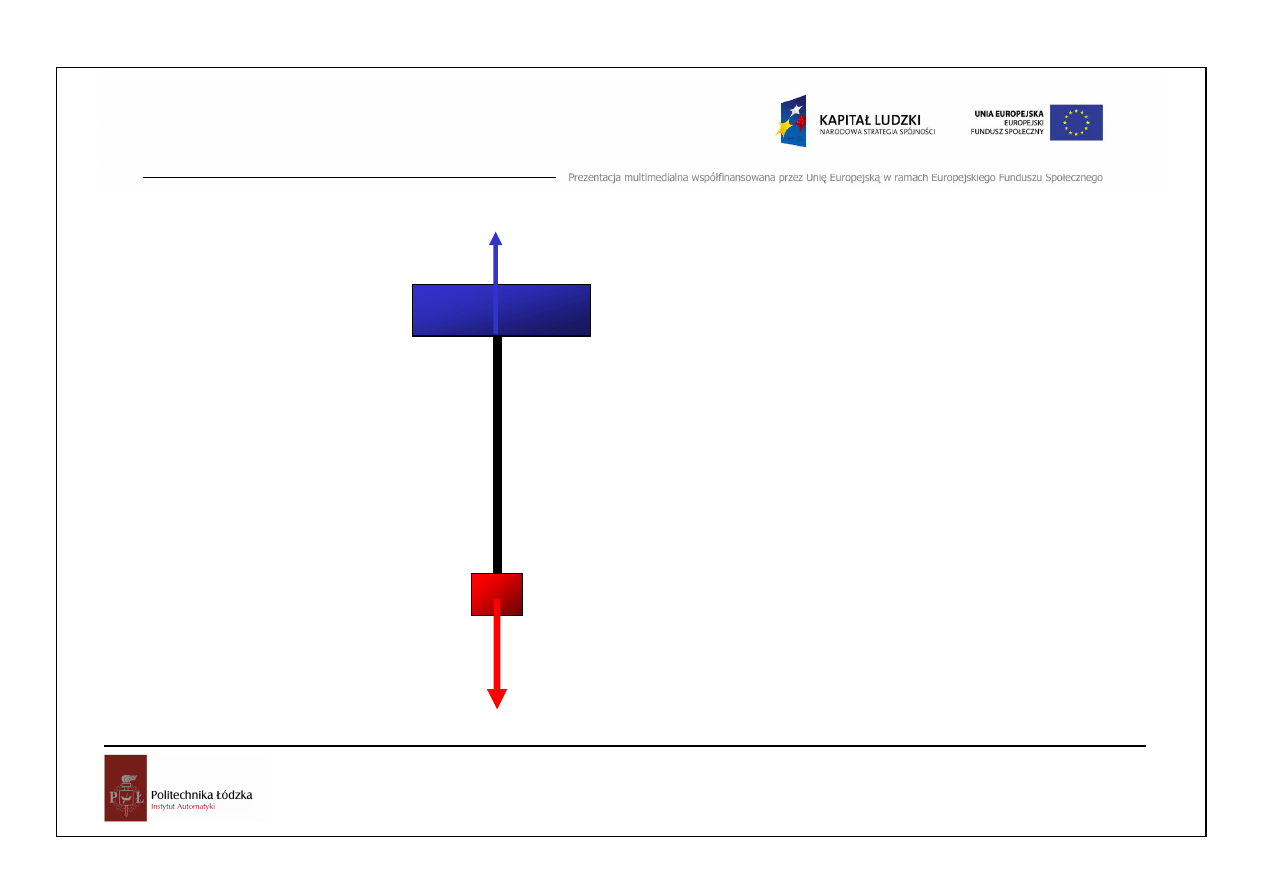
Reakcja wi
ę
zów (zawieszenia) ci
ę
gna
G
R
13
Mechanika i …
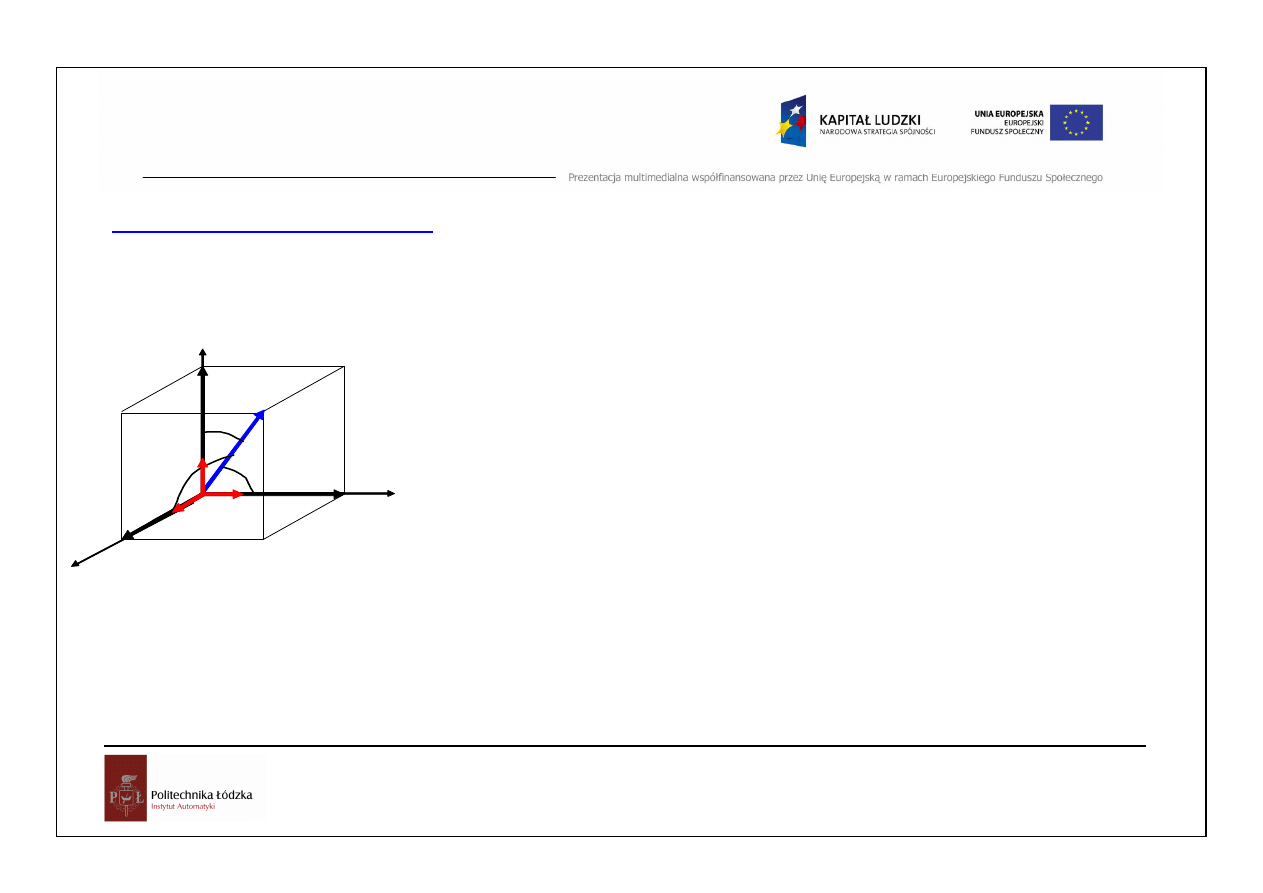
Podstawy algebry wektorów
1
cos
cos
;
cos
;
cos
2
2
2
=
+
+
−
=
=
=
n
m
l
kierunkowe
inusy
n
m
l
γ
β
α
P
i
P
ix
P
iz
P
iy
z
x
y
α
αα
α
i
ββββ
i
γγγγ
i
k
i
j
k
P
j
P
i
P
P
iz
iy
ix
i
r
r
r
r
⋅
+
⋅
+
⋅
=
Wektor jest par
ą
uporz
ą
dkowan
ą
punktów w przestrzeni. Opisuje wielko
ść
fizyczn
ą
, która ma warto
ść
liczbow
ą
, kierunek i zwrot, oraz której dodawanie zdefiniowane jest przez zasad
ę
równoległoboku.
i, j, k, - wersory (wektory jednostkowe) w układzie współrz
ę
dnych x,y,z
14
Mechanika i …
Suma dwu wektorów (zdefiniowana przez zasad
ę
równoległoboku):
k
B
j
B
i
B
k
A
j
A
i
A
B
A
z
y
x
z
y
x
r
r
r
r
r
r
r
r
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
+
z
z
z
y
y
y
x
x
x
z
z
y
y
x
x
B
A
C
B
A
C
B
A
C
k
B
A
j
B
A
i
B
A
B
A
C
+
=
+
=
+
=
⋅
+
+
⋅
+
+
⋅
+
=
+
=
r
r
r
r
r
r
)
(
)
(
)
(
x
y
A
A
x
⋅⋅⋅⋅
i
C
α
i
j
B
x
⋅⋅⋅⋅
i
A
y
⋅⋅⋅⋅
j
B
y
⋅⋅⋅⋅
j
B
x
⋅⋅⋅⋅
i
B
Suma dwóch wektorów na płaszczy
ź
nie
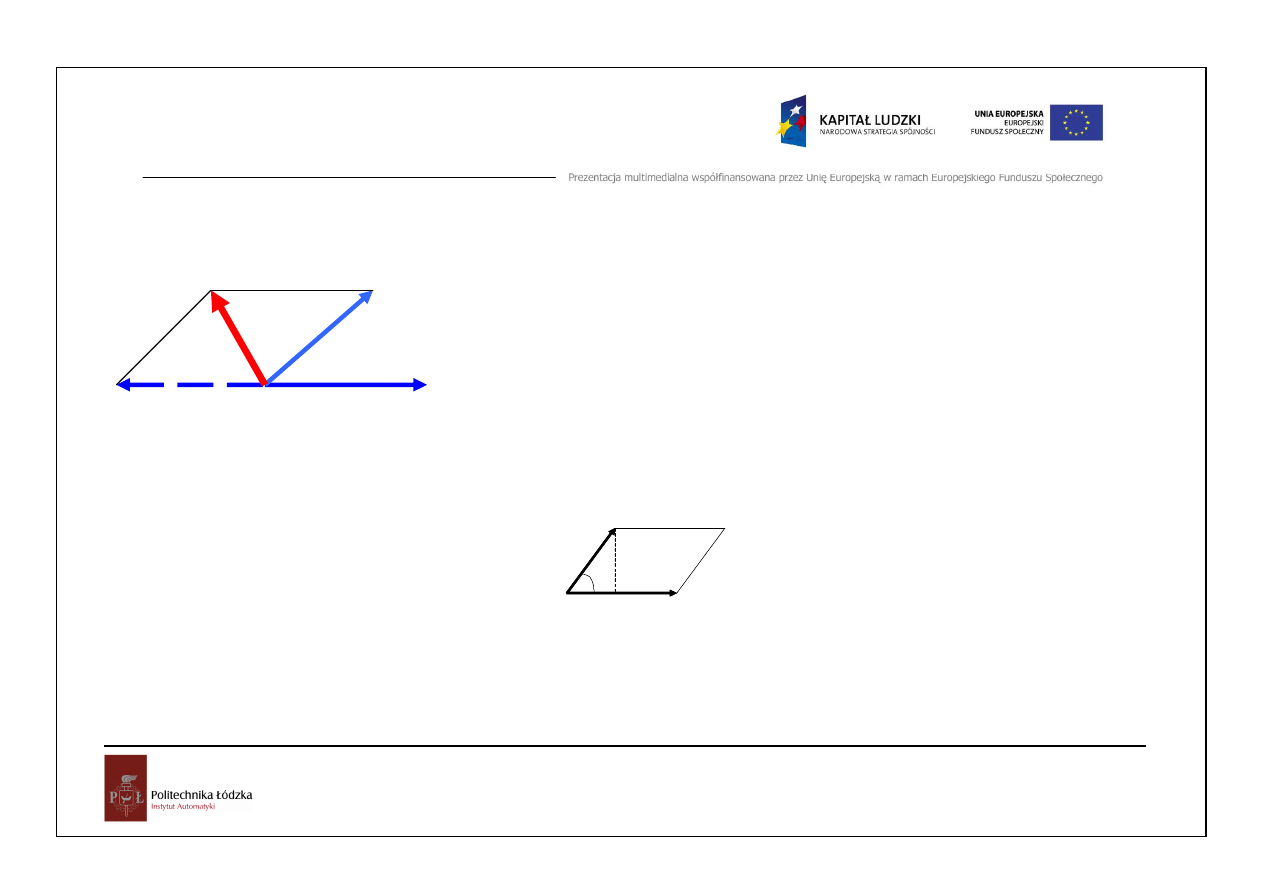
15
Mechanika i …
Ró
Ŝ
nica dwu wektorów:
)
( B
A
B
A
C
r
r
r
r
r
−
+
=
−
=
-B – wektor przeciwny do wektora B
A
-B B
Iloczyn skalarny dwóch wektorów:
ϕ
cos
AB
B
A
=
•
r
v
A
B
ϕϕϕϕ
z
z
y
y
x
B
A
B
A
B
A
B
A
x
+
+
=
•
v
v
16
Mechanika i …
Iloczyn wektorowy dwóch wektorów:
C
A
B
C=A
x
B
ϕϕϕϕ
i
r
j
r
k
r
C
A
B
ϕϕϕϕ
h=|B| sin
ϕ
C=|A| |B| sin
ϕ
Iloczynem wektorowym wektorów
A
r
i
B
r
nazywamy wektor
C
r
, który ma nast
ę
puj
ą
ce własno
ś
ci:
1. wektor
C
r
jest prostopadły do wektorów
A
r
i
B
r
2. warto
ść
bezwzgl
ę
dna wektora
C
r
wynosi
ϕ
sin
B
A
C
⋅
=
3.
C
r
tworzy z wektorami
A
r
i
B
r
układ prawoskr
ę
tny, tzn. zwrot iloczynu wektorowego okre
ś
la reguła „prawej dłoni”
Wektor C mo
Ŝ
na te
Ŝ
wyrazi
ć
za pomoc
ą
wyznacznika macierzy :
z
y
x
z
y
x
B
B
B
A
A
A
k
j
i
C
r
r
r
r
det
=