POLITECHNIKA RADOMSKA

im. KAZIMIERZA PUŁASKIEGO

PROJEKT NR.1

PROJEKT MECHANIZMU ŚRUBOWEGO

Wykonał:

Gregorczyk Krzysztof

Wydział: Mechaniczny

Studia:magisterskie

Kierunek:Mechanika i Budowa Maszyn

Rok studiów:III Semestr:V

Grupa:A1

Sprawdził:

dr inż. LESZEK SARNOWICZ

Radom 2003

Kinematyka konstrukcji podnośnika nożycowego podwójnego

1. założenia konstrukcyjne:(szkic konstrukcji)

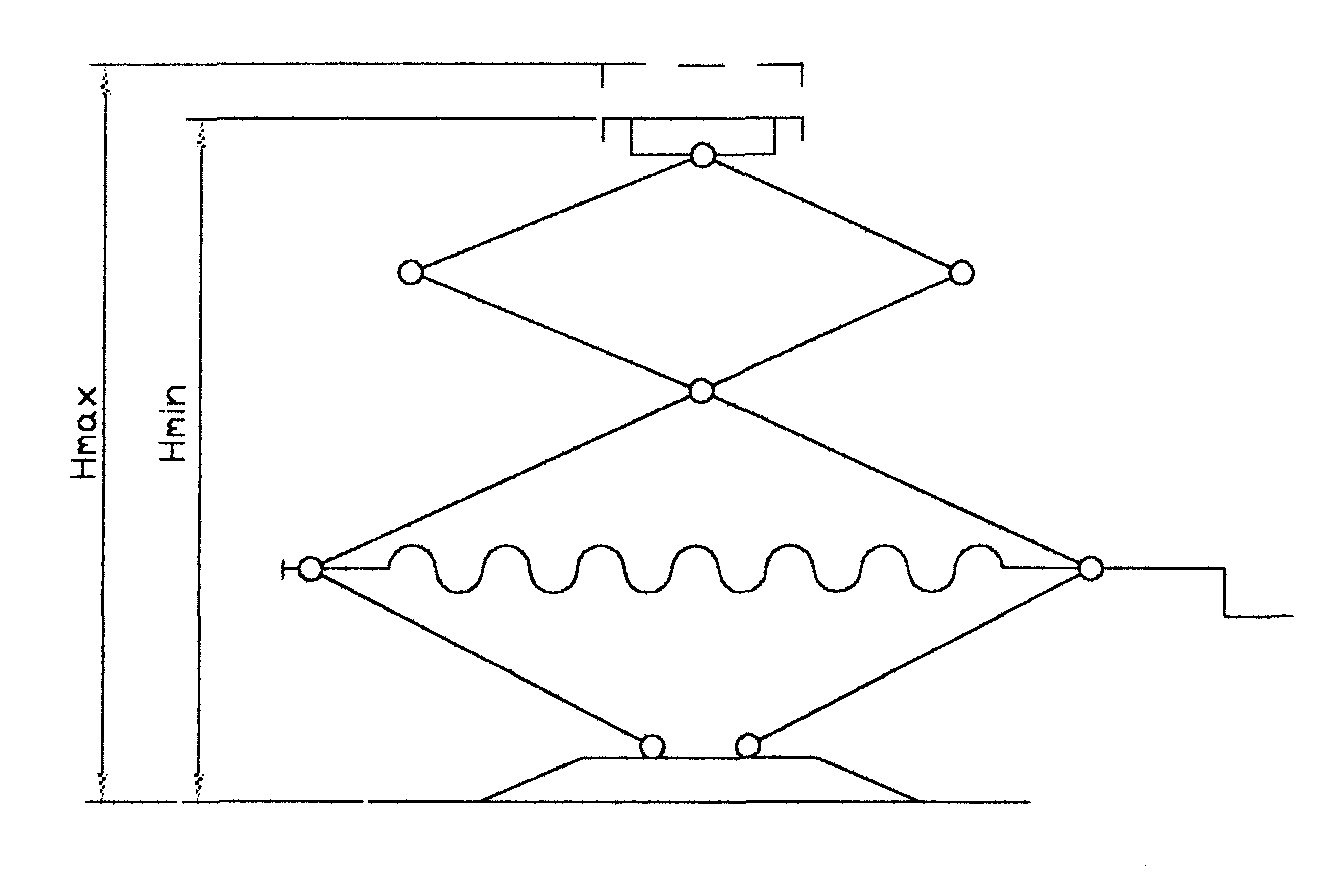
• najmniejsza wysokość podnośnika H_min=100mm

• największa wysokość podnośnika H_max=400mm

• obciążenie Q=10[kN]

b)określam zależności wymiarowe aby spełnić założenia H_min i H_max

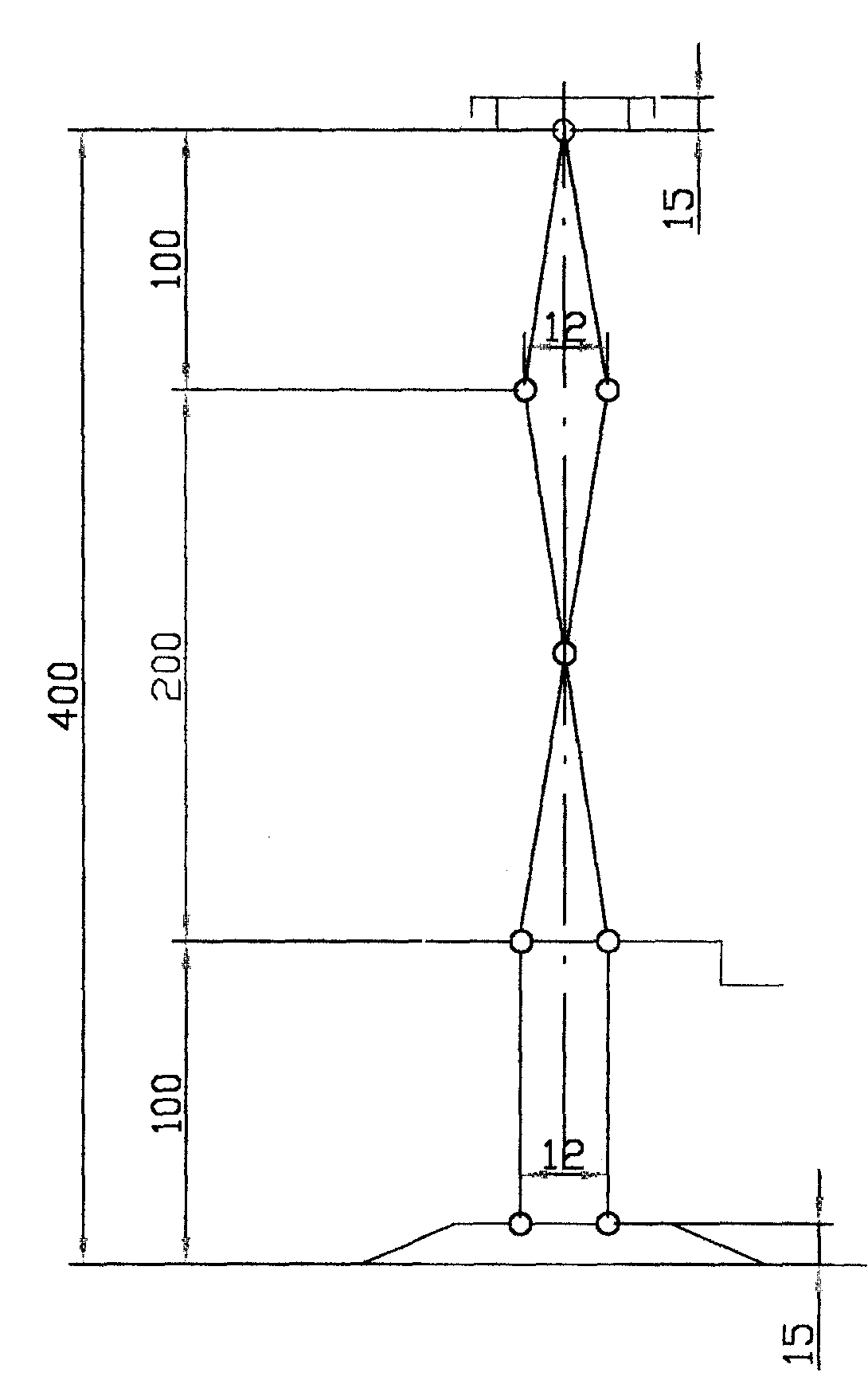
a²+b²=c² 6²+85²=c²

c²=7261

c=85[mm]

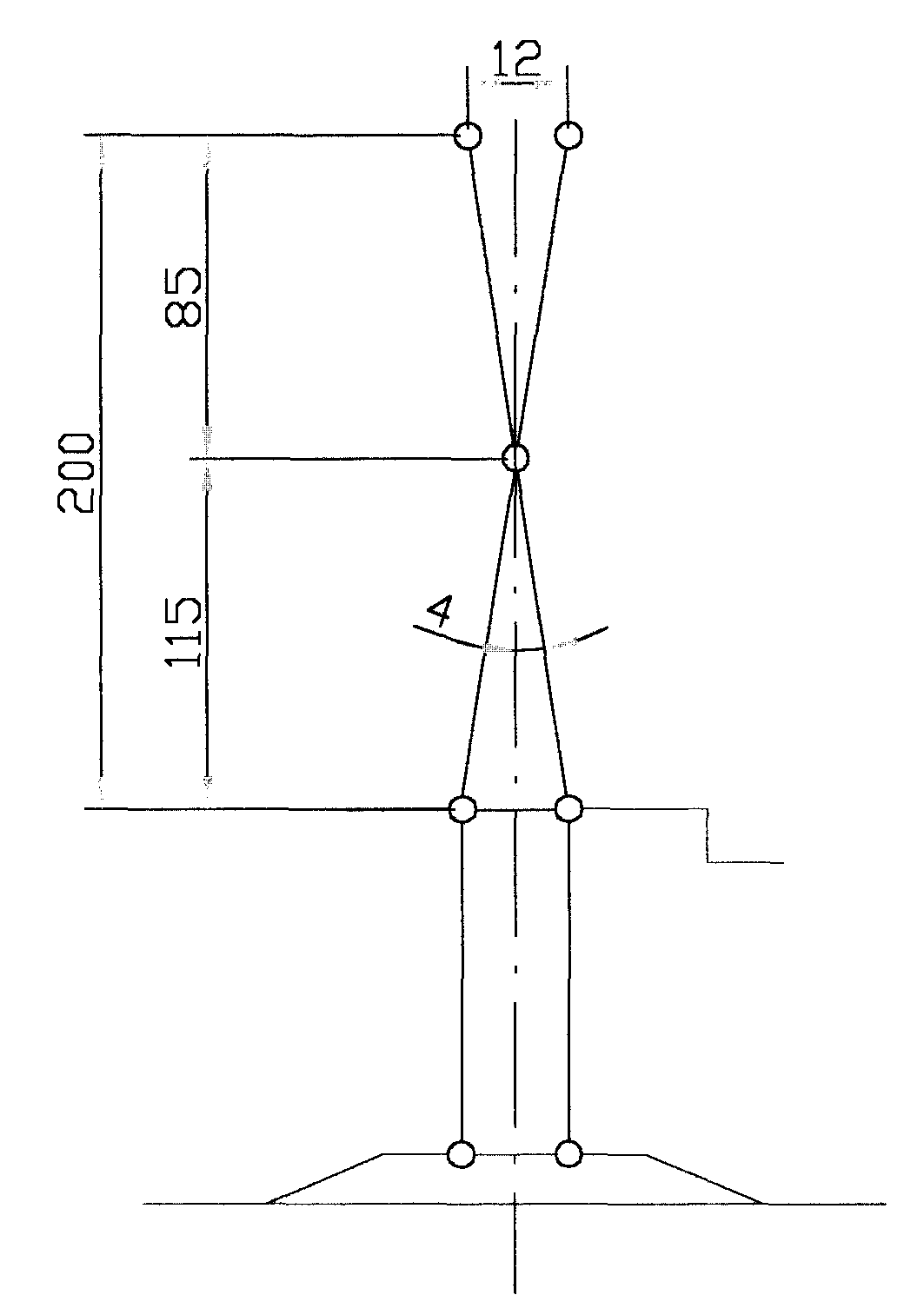
Ze względu na mały kąt α=
długości ramion przyjmuję jako wysokość w położeniu max wznosu.

c)obliczam wartość siły Q działającej na śrubę w najniższym położeniu podnośnika

-analiza sił

∑:Fx S₁cosα-S₂cosα=0 ⇒S₁=S₂ β=2α

∑:F_y S₁sinα-S₂cosα+Q=0

Ssinα+Ssinα=Q

Obliczam wartość siły wypadkowej F działającej na śrubę

d)obliczam minimalny kąt powyżej którego zacznie się podnoszenie ciężaru Q=10[kN]

2H₂+2H₁+30=100 /:2

H₁+H₂+15=50

H₁=35-H₂

⇒
⇒ 85H₂=115(35-H₂)

85H₂+115H₂=115*35

H₂=
=20[mm]

H₁=35-20=15[mm]

sinα=
=0.1739 ⇒ α=10⁰ ⇒ β=2α

F=

Uwaga: Ze względu na duży rozrzut wartości H_min i H_max mamy dużą wartość wznosu W=300[mm] przy określonym parametrze H_min = 100[mm] musimy znacznie zmniejszyć wartość kąta α . Zmniejszenie tego kąta przy pełnym obciążeniu powoduje wzrost siły rozciągającej śrubę F do nieskończoności .

W związku z zasadami technologicznymi bez sensu buło by stosowanie podnośnika który podniesie ciężar Q=10[kN] , a siła działająca na śrubę przy minimalnym kącie α jest około sześciokrotnie większa . W związku z tym zwiększam minimalną wysokość podnośnika od której zaczniemy podnosić ciężar Q do H_min =150[mm] .

2H₂+2H₁+30=150

H₁=60-H₂

_⇒
⇒ 85H₂=115(60-H₂)

85H₂+115H₂=115*60

H₂=34.5[mm]≈35[mm]

H₁=70-35=35[mm]

sinα=
=0.3043 α=18^o β=36^o

F=
[kN]=

=
[kN]=
[kN]=29.29[kN]≈30[kN]

Obliczenia wytrzymałościowe

Dane wejściowe:

Udzwig Q = 10[kN]

Wysokość podnoszenia: h = 100÷400 [mm]

Typ produkcji: seryjna

Typ mechanizmu: podnośnik śrubowo-nożycowy

Dane	Obliczenia	Wynik
Q=10[kN] kr=325[Mpa]	Obliczam wstępną średnicy rdzenia śruby zakładając materiał śruby-20H -z warunku wytrzymałościowego na rozciąganie obliczam średnicę rdzenia śruby: -przy Fr= ,stąd średnica rdzenia wynosi :	dr =11.5 [mm]
dr=11.5mm	2.Dobieramy gwint według PN-79/M-02017 gwint trapezowy smetrycznyTr=16x4 (dr=11.5mm;d=16mm;d2=14mm)	Tr16×4
P=4[mm] d2=14[mm] μ=0.1 αr=15^°	3.Obliczam samohamowność gwintu -obliczenie kąta pochylenia linii śrubowej -obliczam pozorny kąt tarcia ρ^': Wniosek: ponieważ zachowany jest warunek ρ^' γ gwint jest samohamowny.	ρ^' γ
Q=10000[N]	4.Obliczam moment skręcającyMsna gwincie: Ms=0.5Qtg(γ+ρ^')d2=0.5⋅10000⋅tg(11.8)⋅14= 0.5⋅10000⋅0.1924⋅14=13468[Nm]	Ms=13468[Nm]
	5. Obliczam naprężenia zastępcze w śrubie z hipotezy Hubera: ; 0.2d =298.5mm^3 m: =41,93[MPa]
	6. Sprawdzenie śruby na wyboczenie ls -długość swobodna śruby , Lx=h+100=100+300=400[mm] s= 237,03≈238 λ - smukłość śruby α = 2- współczynnik zamocowania ix - ramię bezwładności Dla smukłości mniejszej od λgr stosujemy wzór Tetmajera-Jasińskiego σkr = a - b*λ Dla smukłości większej od λgr stosujemy wzór Eulera σkr=368,52 Obliczamy rzeczywiste naprężenia w przekroju rdzenia śruby Sprawdzamy współczynnik bezpieczeństwa = xw=8,78, xw= (6÷9) jeżeli warunek nie jest spełniony, zwiększamy średnicę śruby i powtarzamy obliczenia. Współczynnik bezpieczeństwa mieści się w granicach normy. Pozostaję przy gwincie Tr16x2.
Q=6000 [N] d2=15 [mm] γ=2,43[^o] ρ'=9,826[^o] Dsr=19,5 μ=0,15	7. Obliczamy moment skręcający Ms Ms = 0,5*Q*tg(γ+ρ')*d2 = 0,5*6000*tg(2,43+9,82)*15 = 1844 [Nmm] MT2=T*0,5*Dsr T= = 866,025 [N] MT2=866,025*0,5*0,0195 = 8,44 [N*m] Ms=0,5*0,015*tg (9,826 + 2,43) = 10+8,44 = 18,44 [Nm] σz= σz= 53 ≤ 95 [MPa]	Ms = 18,44 [Nm]
Q=6000 [N]	8. Sprawdzamy naprężenia zastępcze σz Ponieważ rdzeń śruby jest ściskany i skręcany naprężenie zastępcze wynosi: ; Przy czym: =41,93[MPa] =48,284 [mm^2] Fr - przekrój rdzenia śruby Fr= Π*8^2= 200,96 [mm^2]
pdop= 0,15kc pdop=21,75 [Mpa]	9. Obliczamy wysokość nakrętki H z warunku na naciski dopuszczalne na zwojach gwintu: , , stąd: =11,71[mm] ze względu na dobre prowadzenie śruby w nakrętce przyjmujemy H=(1,2÷2,5)d Sprawdzamy ilość zwojów nakrętki n-liczba czynnych zwojów Obliczam ostateczną wysokość nakrętki: H>P*(n+2)+2+2=2*10+4=24[mm]
	10. Obliczanie średnicy zewnętrznej (minimalnej) nakrętki : D0=D+(4÷10) [mm] D0=16,5+7=23,5 [mm] , , , =25,03 [mm] Do celów konstrukcyjnych przyjmuję Dn= 30 [mm]	D0=23,5 [mm] Dn=30 [mm]
	11
Ms=18,44 [Nm] Fr=100[mm^2]	12. Obliczanie długości pokrętła =0,1844 Ms=Mc1 + MT Fr - przekrój rdzenia śruby l'= 190[mm] - rzeczywista długość pokrętła	L=190[mm]
	13. Obliczenie średnicy pokrętła Dobieram materiał pokrętła stal 45: Mg= Fr*l' Dpokr=9,5[mm] ≈10[mm] l' - praktyczna długość pokrętła
d3 = 11,9	14. Obliczam sworzeń ramienia Sworzeń pasowany ciasno jest narażony ciasno na ścięcie w dwóch przekrojach, zatem: τts=59,71≤65[Mpa] Warunek spełniony.	D = 16,66 [mm]
	15.Obliczam ramię podnośnika. Ramię podnośnika obciążone jest momentem gnącym. Dobieram materiał ramienia stal 45 Mg = P * l Mg=6000*0,1=600[Nm] σr=61728395[Pa]≈62[MPa] 205≥62 Warunek spełniony.	dkor =5,95 [mm]
L=360[mm]	16.Obliczam smukłość korpusu Lw=2*L=720[mm] S= ix- promień bezwładności Lw- długość wyboczeniowa I - moment bezwładności F - pole przekroju b=44[mm] h=39[mm] ix=0,33 s=2,18<100
Q=5000 [N] r = 13[mm]	16. Sprawdzenie nacisku na podłoże pdop = 0,1 MPa F'= Π*r^2 - pole nacisku	p = 0,094 [MPa]

L/d>10 to wtedy element nie jest wybaczany

Materiał stal		Rm min. [MPa]	Re min [MPa]	Naprężenia dopuszczalne [MPa]
				kr≈kc	krj≈kcj	krc	kg	kgj	kgo	ks≈kt	ksj≈ktj	kso≈kto
45	600		355	195	102	57	230	144	78	128	95	46

---