Sem. VI Gliwice 4.04.2006 r.
Gr.E1
rok akademicki 2005/2006
Laboratorium z techniki cyfrowej i mikroprocesorowej
Temat: Liczniki asynchroniczne
Sekcja 7
Tomasz Kopeć
Mariusz Witek
Wstęp.
Liczniki asynchroniczne należą do grupy układów sekwencyjnych, więc stan ich
wejść zależy od stanu układu. Liczbę różnych stanów przyjmowanych przez licznik pod wpływem impulsów wejściowych nazywa się pojemnością licznika. Badane liczniki były tworzone przez odpowiednie połączenia przerzutników JK i dlatego ich pojemność zawiera się w przedziale (1;2n) gdzie n jest ilością użytych przerzutników. Przy budowie przerzutników wykorzystuje się różne sposoby wyzwalania np. wyzwalanie zboczem lub poziomem. W naszym ćwiczeniu liczniki były wyzwalane poziomem i są budowane na podstawie przerzutników MS (Master- Slave), a sygnał zegarowy z reguły podawany na przerzutnik wejściowy a stany pozostałych zależą od stanu przerzutnika wcześniejszego. Powoduje to wzrost czasu zliczania co jest główną wadą tych układów.
Cel ćwiczenia.
Celem ćwiczenia jest zapoznanie się z układami liczników asynchronicznych,
poznanie ich budowy oraz zasad projektowania jak i zapoznanie się ze scalonym licznikiem binarnym rewersyjnym 7493.i 7492
Tablica stanów dla przerzutnika JK.
J1 |
K1 |
|
0 |
X |
|
1 |
X |
|
X |
0 |
|
X |
1 |
|
Model licznika asynchronicznego modulo 3.
Schemat układu: (ze sprzężeniem zerującym bezpośrednio)
Przebiegi czasowe:
3.1 Licznik modulo 6 zliczający w przód
CLk |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Q0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
Q1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
Q2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
3.2 Licznik modulo 8 zliczający w tył :

CLk |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
Q0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
Q1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Q2 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
3.3 Licznik asynchroniczny modulo 9:
Schemat układu:
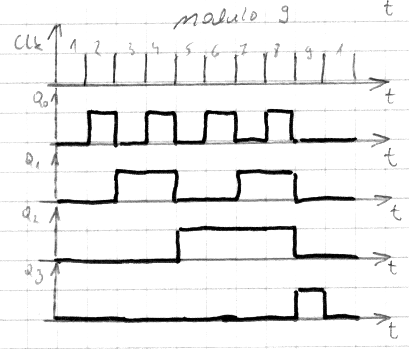
Przebiegi czasowe:
CLk |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Q0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
Q1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Q2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Q3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
Licznik asynchroniczny modulo 10:
Schemat układu:
CLk |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Q0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
Q1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Q2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
Q3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
3.3 .Modelowanie liczników metodą rozkładu.
Zasada modelowania metodą rozkładów:
dla tak podanej zasady możemy zamodelować licznik modulo 5
(2*2+1):
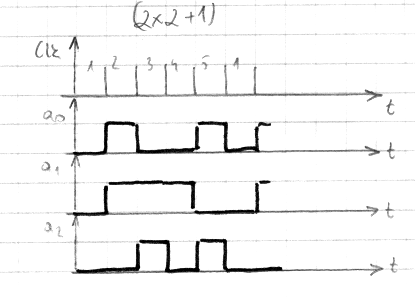
Tabela stanów
Lp. |
QA |
QB |
QC |
1 |
1 |
1 |
0 |
2 |
0 |
1 |
1 |
3 |
0 |
1 |
0 |
4 |
1 |
0 |
1 |
5 |
0 |
0 |
0 |
3.4 .Licznik modulo 9(2*4+1)
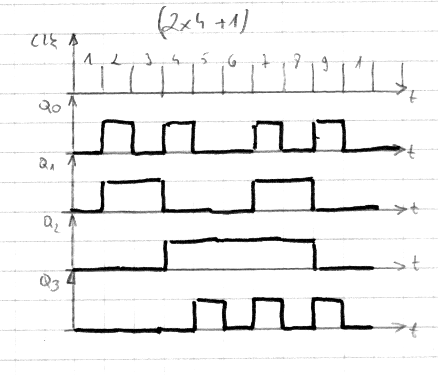
Tabela stanów
Lp. |
QA |
QB |
QC |
QD |
1 |
1 |
1 |
0 |
0 |
2 |
0 |
1 |
0 |
0 |
3 |
1 |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
1 |
5 |
0 |
0 |
1 |
0 |
6 |
1 |
1 |
1 |
1 |
7 |
0 |
1 |
1 |
0 |
8 |
1 |
0 |
0 |
1 |
9 |
0 |
0 |
0 |
0 |
Licznik modulo 10 ze strukturą (2n+1)
CLk |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
Q0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
Q1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
Q2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Q3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
4 Asynchroniczny licznik 7492
Schemat układu: w układzie 6421
Tablica stanów dla licznika:
|
QA |
QB |
QC |
QD |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
2 |
0 |
1 |
0 |
0 |
3 |
1 |
1 |
0 |
0 |
4 |
0 |
0 |
1 |
0 |
5 |
1 |
0 |
1 |
0 |
6 |
0 |
0 |
0 |
1 |
7 |
1 |
0 |
0 |
1 |
8 |
0 |
1 |
0 |
1 |
9 |
1 |
1 |
0 |
1 |
10 |
0 |
0 |
1 |
1 |
11 |
1 |
0 |
1 |
1 |
4.1. Model licznika 7492 w systemie 6321
Tabela stanu:
|
QA |
QB |
QC |
QD |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
0 |
1 |
4 |
0 |
1 |
0 |
1 |
5 |
0 |
0 |
1 |
1 |
6 |
1 |
0 |
0 |
0 |
7 |
1 |
1 |
0 |
0 |
8 |
1 |
0 |
1 |
0 |
9 |
1 |
0 |
0 |
1 |
10 |
1 |
1 |
0 |
1 |
11 |
1 |
0 |
1 |
1 |
W tym liczniku nie można zrealizować stanu 10 i 11
Realizacja modulo 5 na liczniku 7492 (6321):
Realizacja modulo 5 na liczniku 7492 (6421):
Realizacja licznika modulo 10 na liczniku 7492 (6421):
Realizacja licznika modulo 9 na liczniku 7492 (6321):
5. Modelowanie licznika modulo 18 jako połączenie licznika 7493 i 7492:
Tablica stanu:
|
Qa |
Qb |
QA |
QB |
QC |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
0 |
1 |
0 |
0 |
0 |
3 |
0 |
0 |
1 |
0 |
0 |
4 |
1 |
0 |
1 |
0 |
0 |
5 |
0 |
1 |
1 |
0 |
0 |
6 |
0 |
0 |
0 |
1 |
0 |
7 |
1 |
0 |
0 |
1 |
0 |
8 |
0 |
1 |
0 |
1 |
0 |
9 |
0 |
0 |
1 |
1 |
0 |
10 |
1 |
0 |
1 |
1 |
0 |
11 |
0 |
1 |
1 |
1 |
0 |
12 |
0 |
0 |
0 |
0 |
1 |
13 |
1 |
0 |
0 |
0 |
1 |
14 |
0 |
1 |
0 |
0 |
1 |
15 |
0 |
0 |
1 |
0 |
1 |
16 |
1 |
0 |
1 |
0 |
1 |
17 |
0 |
1 |
1 |
0 |
1 |
6.Wnioski.
Po poznaniu metod modulowania liczników asynchronicznych i zasad jakimi należy się kierować stwierdzono iż można w sposób bardzo prosty wyznaczyć strukturę licznika opartego na przerzutnikach JK i odpowiednich połączeń wyjść z wejściami. Zauważono możliwość tworzenia liczników modulo n jednak sprawa modelowania komplikuje się w miarę wzrostu ilości przerzutników jak i sposobu modelowania. Zliczanie w liczniku asynchronicznym następuje kolejno po sobie od najmłodszego przerzutnika do najstarszego kolejno przez wszystkie możliwe kombinacje jednak zmiana stanu następnego w kolejce przerzutnika następuje gdy wszystkie młodsze przerzutniki na swym wyjściu mają stan wysoki „1”, bo wówczas wtedy podawany jest na kolejny przerzutnik impuls zegarowy. Powoduje to wzrost czasu zliczania co jest główną wadą tych układów. W przypadku liczników z rozkładem na czynniki zauważenie kolejności zmian zliczania jest trudniejsza, co można zaobserwować w badanych przykładach na przebiegach czasowych przedstawionych na poszczególnych diagramach.
W układzie 7493 licznik zachowywał się jak zwykły licznik asynchroniczny, zaś 7492 (modulo 12) był licznikiem ograniczonym ze względów technicznych. Połączenie szeregowe tych dwóch liczników pozwala na budowę liczników n*m .
Liczniki asynchroniczne są wolniejsze od liczników synchronicznych. Spowodowane jest to faktem, że zmiana stanu licznika następnego powodowana jest dopiero przez zmianę stanu na wyjściu licznika poprzedniego (sygnał taktujący podawany jest z wyjścia Q lub
przerzutnika poprzedniego a nie ze wspólnej linii zegarowej dla wszystkich przerzutników).
Cechuje je łatwość zwiększania ich pojemności oraz konstrukcji dowolnego licznika modulo N na ich podstawie. Licznik modulo 13 został zbudowany przy użyciu bramki NAND.
Liczniki modulo 5, 9,10 zbudowane na podstawie struktury (2n+1) są licznikami których konstrukcja modułowa predysponuje je do łączenia w liczniki o większych pojemnościach. Ich kod wyjściowy nie jest kodem binarnym, więc informacje z wyjścia takiego licznika muszą zostać poddane dodatkowej obróbce lub wykorzystane bezpośrednio przez urządzenie akceptujące taką formę binarnej informacji.
Licznik modulo 10 ze strukturą (2n+1) jest to zmodyfikowany licznik modulo 5, który taktowany jest poprzez podzielnik częstotliwości (pojedynczy przerzutnik JK Master-Slave).
Laboratorium z techniki cyfrowej i mikroprocesorowej - LICZNIKI SYNCHRONICZNE 1
Wyszukiwarka
Podobne podstrony:
liczniki asynchroniczne nasze,moja
liczniki asynchroniczne nasze,moja1
liczniki asynchroniczne
Ćw. 11-Liczniki asynchroniczne TTL, Politechnika Lubelska
badanie licznikow asynchronicznych
Ćw. 11- Liczniki asynchroniczne TTL, Politechnika Lubelska
Laborki z elektroniki, ED 4 - Liczniki asynchroniczne TTL, Laboratorium Podstaw Elektroniki Politech
Badanie licznikow asynchroniczn Nieznany (2)
SURDOPED nasze
W 5g PLC LICZNIKI
PA2 5 przerzutniki asynchr
Nasze opracowanie pytań 1 40
nasze forum 1 2 [2005] hipoterapia i dogoterapia
JONY UJEMNE A NASZE ZDROWIE
więcej podobnych podstron