PODZIAŁ PŁYNÓW

Płyny - w odróżnieniu od ciał stałych zmieniają swój kształt pod działaniem dostatecznie małych sił mechanicznych

- ciecze ρ=const

- gazy ρ = var

kryterium - zmiana objętości

ciecze - płyny zachowujące niemal stałą objętość pod działaniem bardzo wielkich sił mechanicznych i przy dostatecznie małych zmianach temperatury

gazy - płyny znacznie zmieniające swą objętość pod wpływem ciśnienia i temperatury

MODELE PŁYNÓW

korzysta się z nich przy rozważaniach problemów mechaniki płynów

 1)  Płyn doskonały - nieściśliwy i nielepki

2) Płyn nieściśliwy i lepki - ciecz rzeczywista oraz gaz przy małych prędkościach

3)   Płyn ściśliwy i nielepki - gaz doskonały

4)   Płyn ściśliwy i lepki - gaz rzeczywisty

Rozkład Maxwella

skąd dalej średnia prędkość cząsteczek

k- stała Boltzmana , R - stała gazowa dla jednego mola gazu, N-liczba Avogadro

lub

Metoda Lagrange'a

 Badanie i opis właściwości fizycznych poruszającego się indywidualnego elementu płynu jako punktu materialnego.Specjalne zmienne - tzw. zmienne Lagrange'a indywidualizujące element płynu, stałe dla każdego elementu płynu, niezależne od czasu i zmiany położenia

 W konsekwencji otrzymamy opis ruchu w postaci funkcjiH = H(a, b, c, t),

gdzie a, b, c, t - zmienne Lagrange'a

 Zmiana a, b, c - powoduje przejście do innego elementu płynu,

zmiana t - zmiana wielkości H w elemencie płynu.

 Równania toru elementu płynu

 x = x(a, b, c, t ) y = y(a, b, c, t) z = z(a, b, c, t)

Prędkość i przyspieszenie

Metoda Eulera - badanie i opis zmian wielkości fizycznych charakteryzujących ruch płynu w poszczególnych punktach przestrzeni (ustalonych punktach przestrzeni)

x, y, z, t - zmienne Eulera

 

H = H(x, y, z, t) - metoda Eulera polega na badaniu pól wielkości fizycznych

 Zwykle badamy przepływy metodą Eulera

 Przejście pomiędzy obu układami

 

Warunek - wyznacznik funkcyjny jakobian różny od zera w żadnym punkcie obszaru

Równanie ZACHOWANIA MASY i równanie CIĄGŁOŚCI

Równanie zachowania masy.Dla objętości płynu zawierającej wciąż te same cząstki płynu postulat ten można zapisać

 

m i ၲ odpowiednio masa i gęstość

Korzystając następnie z równań analizy wektorowej można równanie to przedstawić w różnej formie

 

 lub z wykorzystaniem pochodnej substancjalnej

 

Gdy gęstość nie jest zależna od czasu

 

Postać całkowa równania zachowania masy

 

 

Jest często wykorzystywana do sporządzenia bilansu masy w objętości kontrolnej V całkując po powierzchniach ograniczających ၳ.

 

W szczególności, gdy gęstość nie jest funkcją czasu otrzymamy

PRAWA EULERA

Prawa Eulera

Całkowita siła powierzchniowa działająca na płyn o objętości V i powierzchni ograniczającej ၳ równa jest

 

natomiast całkowita siła zewnętrzna działająca na płyn o objętości V dana jest następującym wzorem

Zasada zachowania pędu postuluje, że suma obu tych sił jest równa różniczce względem czasu pędu płynu.

A zatem:

1. prawo Eulera:

Rozważmy dalej moment obrotowy a w szczególności jego bilans na elemencie płynu

2. prawo Eulera:

 

Suma momentów obrotowych działających na element płynu o objętości V i ograniczonego powierzchnią ၳ jest równa różniczce względem czasu momentu pędu płynu.

Prawa Eulera są rozszerzeniem praw Newtona dotyczących materialnego sztywnego punktu na przypadek ruchu ośrodka ciągłego.

PRAWA CAUCHY'EGO

Pierwsze prawo Cauchy'ego jest odpowiednikiem pierwszego prawa Eulera przy czym zamiast wektorem naprężeń to operuje składowymi tensora naprężeń T

Korzystając z twierdzenia Greena - Gaussa - Ostrogradskiego możemy napisać

 

Podstawiając do równania Eulera otrzymamy

 

Wykorzystując dalej wzory z poprzednich rozdziałów, w szczególności równanie ciągłościთ ბT dywergencja tensora jest wektorem

Jest to równanie ruchu płynu, nazywane też równaniem różniczkowym bilansu pędu lub też pierwszym prawem Cauchy'ego. Są to w zasadzie trzy równania na każdą składową wektorową თბT = Tij, i

DRUGIE PRAWO CAUCHY'EGO

Drugie prawo Cauchy'ego jest odpowiednikiem drugiego prawa Eulera i dotyczy bilansu momentu obrotowego obszaru płynnego zapisanego przy wykorzystaniu składowych tensora naprężeń. Po pewnych przekształceniach otrzymamy

 

Na mocy pierwszego prawa Cauchy'ego lewa strona jest równa zeru, skąd natychmiast wypływa wniosek

ၥijk Tij = 0

a więc Tij = Tji

  Jest to zapis drugiego prawa Cauchy'ego, że warunkiem koniecznym i dostatecznym zachowania momentu obrotu w płynie jest symetria tensora naprężeń. Konsekwencją tego prawa jest wniosek, że do pełnego określenia tensora naprężeń w płynie wystarczy znajomość sześciu z dziewięciu jego składowych tzn. trzech normalnych i trzech stycznych.

PŁYN STOKESOWSKI

Dla płynu stokesowskiego tensor naprężeń

 

 i jest ciągłą funkcją tensora deformacji D i lokalnego stanu termodynamicznego (ciśnienia p). Tensor naprężeń Tij w płynie stokesowskim nie zależy jawnie od położenia r, a zatem płyn jest homogeniczny.Płyn stokesowski jest ponadto izotropowy tzn. ma jednakowe właściwości we wszystkich kierunkach.Jeśli w płynie nie ma deformacji, to tensor naprężeń lepkich jest równy zeru, a naprężenie jest ciśnieniem hydrostatycznym lub termostatycznym.

Tensor naprężeń lepkich

 

Z warunku na znikanie Pij= 0 gdy Dij= 0 wynika również ၡ = 0

Zatem:

PŁYN NEWTONOWSKI

Jest to liniowy płyn stokesowski, a więc ၧ = 0

Tij = (-p+ၡ)I + ၢ D

Tensor naprężeń lepkich:

Pij = ၬ(თბ u) ၤij + 2ၭ Dij

ၭ - współczynnik proporcjonalności, lepkości

 Tensor naprężeń: Tij = (-p + თბၬ u) I + 2ၭ Dij

 Przy omawianiu ciśnienia hydro- i termostatycznego powiedziano, że wartość średnia naprężeń normalnych wynosi

Dla płynu nieściśliwego div u = 0, თბ u = 0

Zatem

i równa się ciśnieniu hydrostatycznemu.

RÓWNANIE RUCHU PŁYNU NEWTONOWSKIEGO

Pierwsze równanie Cauchy'ego jest równaniem ruchu płynu

 

nie wyróżniającym żadnego modelu płynu. 

Jeżeli podstawimy do niego równanie konstytutywne płynu newtonowskiego, to otrzymamy równania Naviera - Stokes'a opisujące ruch płynu newtonowskiego

Zatem:

PODSTAWOWE ZAGADNIENIE MECHANIKI PŁYNÓW

Równanie ciągłości

Równanie ruchu

Równanie energii

Równanie momentu ruchu wykorzystano do ustalenia symetryczności tensora naprężeń T

1)Równanie stanu

ၲ = ၲ(R, ၱ, p), p = ၲ R ၱ , ၲ = const

ၲ = ၲ(p) barotropowy płyn

2) Równanie wytwarzania energii

3) Pole sił masowych

q = q(ၲ, ၱ, p, t)

F(Fx, Fy, Fz) = F(x, y, z, t) znane pole

q = 0

F=0,

Strumień ciepła przechodzący przez powierzchnię ciała stałego określa się na powierzchni ciała zakładając rozkład temperatury, bądź składową gradientu temperatury w kierunku prostopadłym do powierzchni.

-ścianka izolowana tj. nieprzenikalna dla ciepła

- stała temperatura powierzchni ciała

q=const - stały strumień ciepła na powierzchni

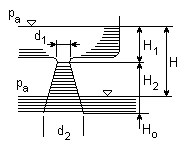
WYPŁYW CIECZY PRZEZ MAŁY OTWÓR

Obliczmy prędkość cieczy wypływającej z otworu

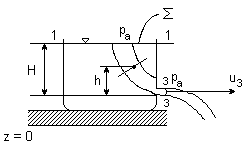
H = const ruch stacjonarny

S = const - przekrój otworu wylotowego

H - środek ciężkości przekroju otworu

pa - ciśnienie atmosferyczne

ၓ - pole lustra wody

l - wymiar liniowy otworu

 S << ၓ, H >> l

Porównując wartości energii w przekroju 1 - 1 i 3 - 3 otrzymamy

Ponieważ: p1 = p3 = pc

 z1 = z0 + H z3 = z0

u1 << u3 bo S << ၓ

 oraz u1 S1 = u3 S3

 Podstawiając otrzymamy:

wzór Torricellego

 Prędkość wypływu przez mały otwór zależy tylko od wysokości H nazywanej wysokością naporu.

Ogólniejszy przypadek wypływu przez mały otwór

H' = const

H'' = const

p' = const

p'' = const

S << ၓ', S <<ၓ''

 Poziom zerowy na wysokości otworu

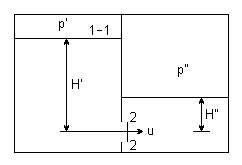
u^'=0 wtedy ρ^' - wypływa do przestrzeni z ρ^''

WYPŁYW PRZEZ DUŻY OTWÓR

Wysokość otworu a tego samego rzędu co wysokość naporu H, H=const

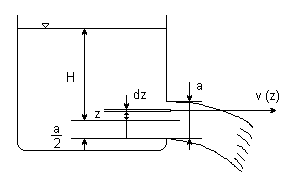
Obliczyć wydatek Q cieczy przez duży prostokątny otwór aთ b w pionowej ścianie zbiiornika, H = const, przepływ ustalony, przekrój otworu wielokrotnie mniejszy od poziomego przekroju zbiornika,

Stosując wzór Torricellego:

Wydatek cieczy Q

Prosty wzór, bo założono jednowymiarowy wypływ, takie założenie zastosowano do zagadnienia, które jest w gruncie rzeczy trójwymiarowe

WYPŁYW QUASI - STACJONARNY

ၳ0- przekrój otworu w dnie naczynia

ၳ (z) - przekrój poziomy funkcją z (wysokości)

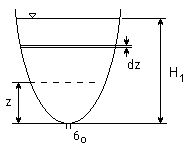
Zbiornik o dowolnym kształcie. Poziom wody opada, obliczmy czas, w jakim ciecz opadnie od H1 do H2. Zagadnienie jest w zasadzie niestacjonarne, zasadniczo nie powinno się stosować do jego rozwiązania równania Bernoulli'ego.

Zastosujemy je jednak zakładając, że wzór Torricellego jest w przybliżeniu słuszny dla dowolnej chwili t pomiędzy 0 i T,

dla dowolnego położenia zwierciadła pomiędzy H1 i H2.

Chwilowy wydatek cieczy:

Jeśli założyć, że poziom cieczy obniży się o dz w czasie dt, to można obliczyć ile cieczy wypłynie ze zbiornika

dla ၳ (z) = const = ၳ,

i dla H₂ = 0

KAWITACJA

Złożone zjawisko przepływowe

  Pęcherzyki pary lub gazu rozpuszczonego w cieczy szybko zanikają po przesunięciu do strefy podwyższonego ciśnienia. Kolaps pęcherzyka (zaniknięcie) niebezpieczny w przypadku wystąpienia przy ściance, gdyż związany z mikrouderzeniem. Związany z tym jest dźwięk, hałas, oraz niszczenie ścianki: tzw. korozja kawitacyjna, mikropęknięcia i utlenianie tlenem zawartym w cieczy oraz przepłukiwanie mikropęknięć, ogólnie: niszczenie materiału.

  Ponadto z kawitacją związana jest strata energii cieczy, tzw. kawitacyjna strata ciśnienia związana z nieodwracalnymi przemianami energii występującymi podczas parowania i skraplania cieczy lub wydzielania się gazu i ponownego rozpuszczania w cieczy.

Przeciwdziałanie: niedopuszczanie do kawitacji.

 pmin > pw

Sposoby niedopuszczenia do kawitacji:

1) kształt urządzenia hydraulicznego taki, aby nie obniżyć ciśnienia do ciśnienia wrzenia

2) podwyższenie ciśnienia statycznego

3) zmniejszyć ciśnienie wrzenia przez obniżenie temperatury cieczy

Współczynnik kawitacji: (liczba kawitacji)

Przykład: określić stosunek średnic rury ssącej, aby w rurze nie wystąpiła kawitacja:

tw = 20oC, p = 1 bar, H1 = 1 m, H2 = 3m, pw = 0,02378 bara

p2 > pw

Jest to jednak warunek na prędkość średnią, w oparciu o lokalne warunki prędkości,

która może być wyższa od wartości średniej. Może wystąpić kawitacja. Stąd jednowymiarowa analiza przepływu może być niewystarczająca, gdyż pomimo spełnienia powyższego warunku może wystąpić kawitacja.

Równanie Bernoulli'ego

Równanie ciągłości strugi

---