AKADEMIA TECHNICZNO- HUMANISTYCZNA

W BIELSKU- BIAŁEJ

WYDZIAŁ NAUK O MATERIAŁACH I ŚRODOWISKU

ROK I SEMESTR I

SPRAWOZDANIE Z LABORATORIUM FIZYKI.

Temat: Wyznaczanie długości fali świetlnej metodą pierścieni Newtona.

WYKONALI:

ARKADIUSZ MALEC

PAWEŁ HABDAS

I. Wstęp teoretyczny:

Promieniowanie świetlne stanowi widzialną część promieniowania elektromagnetycznego i są one falami poprzecznymi. Przyjmuje się, że w powietrzu prędkość światła jest praktycznie równa prędkości światła w próżni i wynosi w przybliżeniu: c ≈ 300 000 km/s. Długość fali (λ) określa najmniejsza odległość pomiędzy punktami o tej samej fazie drgań. Zakres długości fal promieniowania świetlnego rozciąga się od λ ≈ 380 nm do λ ≈ 780 nm.

Interferencją nazywamy nakładanie się fal powodujące zmniejszenie lub zwiększenie amplitudy fali wypadkowej w zależności od różnicy faz fal składowych. Zakładamy przy tym, że spełniona jest zasada superpozycji, tzn. że zaburzenie wypadkowe jest równe sumie poszczególnych zaburzeń falowych.

Światło padając na soczewkę płasko - wypukłą częściowo odbija się od jej wewnętrznej powierzchni, częściowo zaś przenika przez cienką warstwę powietrza i odbija się od płytki szklanej (rys.1). Dzięki tej różnicy dróg tworzą się prążki interferencyjne w kształcie pierścieni (rys.2). Prążki te obserwuje się przez mikroskop ustawiony tak, by jego oś optyczna była równoległa do osi optycznej soczewki. Średnice pierścieni zależne są od promienia R krzywizny soczewki oraz od długości fali światła padającego na soczewkę.

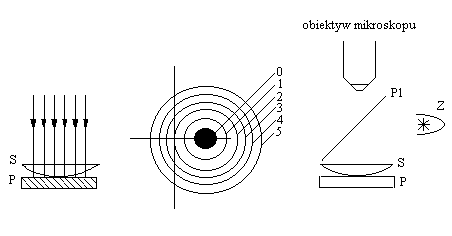
Rys.1. Rys.2. Rys.3

Zależność tę opisuje poniższy wzór:

gdzie: d_k - średnica k-tego pierścienia

R - promień krzywizny soczewki

k - kolejny numer pierścienia

Z powyższego wynika również, że zależność pomiędzy kwadratami średnic kolejnych pierścieni d_k² i ich numerami k, jest zależnością liniową.

Dopasowując zatem do eksperymentalnej zależności d_k²=f(k) prostą regresji liniowej y=ax+b można, na podstawie współczynnika a tej prostej, wyznaczyć długość fali świetlnej. Współczynnik a prostej regresji, jak wynika z powyższego wzoru będzie wówczas określony jako:

Długość fali λ, po odpowiednim przekształceniu równania, wyznacza się ze wzoru:

gdzie: a - współczynnik prostej regresji,

R - promień krzywizny soczewki.

II. Przebieg ćwiczenia:

1. Cel ćwiczenia.

Celem ćwiczenia było zapoznanie się ze sposobem wyznaczania długości fali świetlnej przy pomocy pierścieni Newtona.

2. Przebieg ćwiczenia.

Do wykonania ćwiczenia wykorzystaliśmy następujące przedmioty:

-mikroskop optyczny,

-soczewka płasko-wypukła i płytka szklana zamocowane w uchwycie na stoliku mikroskopu.

-czujnik zegarowy

-lampa sodowa w obudowie.

-zasilacz

Pierwszym krokiem w wykonaniu tego ćwiczenia było włączenie zasilacza lampy sodowej i odczekanie aż lampa zaczęła świecić jednorodnym żółtym światłem.

W trakcie nagrzewania się lampy sodowej zaznajomiliśmy się z położeniem i działaniem pokręteł regulacyjnych mikroskopu oraz z określaniem wartości przesunięcia wzdłużnego stolika przy pomocy czujnika zegarowego.

Po odpowiednim nagrzaniu się lampy sodowej ustawiliśmy ją blisko stolika mikroskopu po czym sprawdziliśmy czy w okularze mikroskopu jest widoczny obraz dyfrakcyjny w postaci pierścieni Newtona.

Następnie przeszliśmy do bezpośredniego pomiaru średnic pierścieni Newtona- indywidualnie dla poszczególnych pierścieni (wariant I). Pomiar wykonaliśmy dziesięciokrotnie. Wyniki pomiarów zanotowaliśmy w tabeli 1 na arkuszu wyników pomiarów (arkusz w załączeniu sprawozdania).

Po zakończeniu pomiaru metodą I (indywidualnie dla poszczególnych pierścieni) przeszliśmy do pomiaru dla całej serii, odczytując kolejno współrzędne skrajnych punktów pierścieni wpierw po jednej, a następnie po drugiej, przeciwległej stronie obrazu (wariant II). Wyniki pomiarów wpisaliśmy do tabeli 2 na arkuszu wyników pomiarów. Dla obu wariantów pomiarów wykreślono charakterystykę d_m² = f(m).

3. Opracowanie wyników pomiarów:

Współczynniki dla prostej regresji: a, Δa, b, Δb dla obu wariantów pomiarów wyznaczyliśmy za pomocą programu komputerowego dostępnego w pracowni fizycznej.

POMIAR I

m	1.	2.	3.	4.	5.	6.	7.	8.	9.	10.
dm[mm]	0.55	0.78	0.86	1.02	1.21	1.44	1.56	1.66	1.72	1.79
dm^2[mm^2]	0.3	0.61	0.74	1.04	1.46	2.07	2.43	2.76	2.96	3.20

R= 0.120 ± 0.001 [m]

Parametry prostej regresji:

a= 0.348 [mm²] b= -0.156 [mm²]

Δa= 0.016 [mm²] Δb= 0.098 [mm²]

Obliczenia dla pomiaru I:

Obliczenie długości fali λ dla żółtej linii światła lampy sodowej:

wzór:

λ =

R=0.120 [m] = 120 [mm]

λ = 0.348/ 4^. 120

λ= 725 [nm]

Obliczenie błędu względnego:

wzór:

Δλ = 40 [nm]

Obliczenie błędu względnego wyrażonego w procentach:

wzór:

δ= (40/ 725) ^. 100%

δ=5.5 %

Końcowy wynik pomiaru 1: λ = 725 ± 40 nm

Oszacowanie względnego odchylenia wyznaczonego w procentach pomiędzy wyznaczoną wartością długości fali λ światła żółtego lampy sodowej a wartością tablicową λ_t żółtej linii promieniowania świetlnego sodu:

wzór:

λ_t = 589 nm

δ_t = ( |725-589| / 589 ) ^. 100% = 23%

δ_t = 23%

POMIAR II

m	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
X [mm]	1.01	0.92	0.85	0.77	0.70	0.65	0.60	0.56	0.51	0.46	0.36	0.28	0.22	0.15	0.05	0
Y [mm]	1.5	1.6	1.7	1.74	1.81	1.89	1.92	1.95	2.01	2.03	2.08	2.11	2.15	2.18	2.21	2.24
dm [mm]	0.49	0.68	0.85	0.97	1.11	1.24	1.32	1.39	1.5	1.57	1.72	1.83	1.93	2.03	2.16	2.24
dm^2 [mm^2]	0.24	0.46	0.72	0.94	1.23	1.54	1.74	1.93	2.25	2.46	2.96	3.35	3.72	4.12	4.67	5.02

R= 0.120 ± 0.001 [m]

Parametry prostej regresji:

a= 0.313 [mm²] b= -0.329 [mm²]

Δa= 0.011 [mm²] Δb= 0.11 [mm²]

Obliczenia dla pomiaru II:

Obliczenie długości fali λ dla żółtej linii światła lampy sodowej:

wzór:

λ =

R=0.120 [m] = 120 [mm]

λ = 0.313 / 4^. 120

λ = 652 [nm]

Obliczenie błędu względnego:

wzór:

Δλ = 29 [nm]

Obliczenie błędu względnego wyrażonego w procentach:

wzór:

δ= (29 / 652) ^. 100%

δ= 4.4 %

Końcowy wynik pomiaru 2: λ = 652 ± 29 nm

Oszacowanie względnego odchylenia wyznaczonego w procentach pomiędzy wyznaczoną wartością długości fali λ światła żółtego lampy sodowej a wartością tablicową λ_t żółtej linii promieniowania świetlnego sodu:

wzór:

λ_t = 589 nm

δ_t = ( |652 - 589| / 589 ) ^. 100%

δ_t = 10.7 %

III. Wnioski:

Lampa sodowa emituje światło żółte, którego widmo składa się z dwóch położonych blisko siebie linii o długościach fal 598,6 nm i 589,0 nm. Wyznaczona przez nas długość fali nieco odbiega od tych wartości i nie mieści się w granicach obliczonego błędu pomiaru.

Pomiar średnic pierścieni był dość trudny ze względu na:

-słabą widoczność pierścieni, co powodowało szybkie zmęczenie oczu,

- dużą trudność w odróżnieniu pierścieni o rzędzie n > 10,

- dużą czułość układu na wpływ czynników zewnętrznych takich jak np. szturchnięcia,

-niedoskonałość mięśni dzięki którym możemy dokonać przesunięcia stolika i doprowadzić do styku kreski z pierścieniem,

Dodatkowym czynnikiem powodującym duży błąd pomiaru jest wciąż nasze małe doświadczenie (jako uczniów) w wykonywaniu ćwiczeń fizycznych a w szczególności tak skomplikowanych jakim było to badanie.

---