Pomiary rezystancji metodą mostkową

Labolatorium z elektroniki

Agnieszka Tuszyńska

30.03.2010 r

Cel ćwiczenia:

Zapoznanie się z mostkiem Wheatstone'a do pomiaru rezystancji oraz jego właściwościami w zastosowaniach jako mostek zrównoważony i wychylony.

1. Mostek zrównoważony

Ocena wpływu na dokładność pomiarów przeprowadzonych z wykorzystaniem mostka Wheastone'a następujących czynników:

- stosunek wartości rezystorów R4/R3 stosowanych w układzie mostka

- napięcie zasilania mostka

- ziarno regulacji rezystancji wzorcowej

W stanie równowagi mostka (U_wy=U_AC=0) jest spełniony warunek:

Jeżeli R₁ jest rezystancją mierzoną, wtedy R₂ jest regulowanym wzorcem rezystancji, a R₃ i R₄ ustalają stosunek. Zmieniając ten stosunek można równoważyć mostek dla różnych wartości mierzonych rezystancji R₁, stosując ten sam wzorzec rezystancji R₂

1a. Układ pomiarowy.

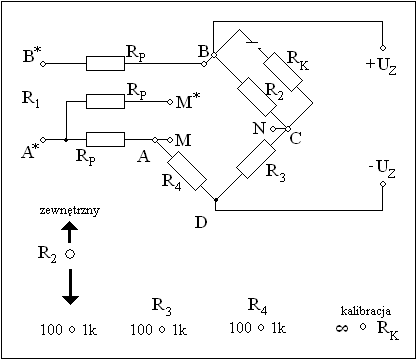
Rys: Makieta mostka Wheatstone'a do pomiaru rezystancji.

1b. Wykorzystane urządzenia:

• Opornik dekadowy, (dla x0,1Ω: ± 0,5%; dla x1Ω: ± 0,1;
  dla x10Ω: ± 0,05; dla x100Ω: ± 0,05; x1kΩ: ± 0,05)

• Mostek rezystancyjny

• Miernik Metex M-4640A, 0.05% rdg +3dgt, Uzakres = 20V.

1c. Przykładowe obliczenia

R₂=100Ω

R₃=R₄=100Ω

=100Ω

R₂=100Ω

R₃/R₄=10Ω

R₂=100Ω

R₃/R₄=0,1Ω

Obliczenia prowadzimy analogicznie dla R₂=1 kΩ oraz dla tych samych stosunków R₃/R_4.

∆U₁=0.05% rdg +3dgt =0,0005*0,000+3*0,001=0,003 [V]

∆U₃=0.05% rdg +3dgt =0,0005*0,001+3*0,001=0,003 [V]

Tabela pomiarów dla mostka zrównoważonego

Lp.	R2 [Ω]	R4/R3 [Ω]	R1 [Ω]	E [V]	UAC [V]	∆ UAC [V]
1	100	1	100	3,0	0,000	0,003
2	100	1	100	4,5	0,000	0,003
3	100	10	1000	3,0	0,001	0,003
4	100	10	1000	4,5	0,001	0,003
5	100	0,1	10	3,0	0,001	0,003
6	100	0,1	10	4,5	0,000	0,003
7	1000	1	1000	3,0	0,001	0,003
8	1000	1	1000	4,5	0,000	0,003
9	1000	10	10000	3,0	0,001	0,003
10	1000	10	10000	4,5	0,001	0,003
11	1000	0,1	100	3,0	0,000	0,003
12	1000	0,1	100	4,5	0,000	0,003

2. Mostek wychyłowy

Do mostka dołączono jako R1 dekadę rezystancyjną, nastawiono R2=R3=R4=100Ω i zrównoważono mostek utrzymując stałą wartość napięcia zasilania równą 4,5V.

Mierzono napięcie wyjściowe mostka w funkcji stosunku Rx/R0, gdzie R0 jest wartością rezystora w stanie zrównoważenia mostka.

W naszym ćwiczeniu R0=1000Ω=1kΩ

Stosunek Rx/R0 zmieniano w sposób równomierny, w granicach 0÷2, 0,9÷1,1 oraz 0,99÷1,01..

Wartości zmierzone przy pomocy woltomierza zestawiono w tabeli i na ich podstawie sporządzono wykresy U_AC=f(Rx/R0).

2a. Przykladowe obliczenia

Rx/Ro=2,0 kΩ/1,0 kΩ=2,0 kΩ

Tabela pomiarów dla mostka wychyłowego

Lp.	0 ÷ 2 [kΩ]			0,9 ÷ 1,1 [kΩ]			0,99 ÷ 1,01 [kΩ]
		Rx [kΩ]	Rx/Ro [kΩ]	U [V]	Rx [kΩ]	Rx/Ro [kΩ]	U [V]	Rx [kΩ]	Rx/Ro [kΩ]	U [V]
1	0,0	0,0	3,924	0,90	0,90	0,038	0,99	0,99	0,000
2	0,2	0,2	1,072	0,91	0,91	0.033	0,991	0,991	0,000
3	0,4	0,4	0,483	0,92	0,92	0,029	0,992	0,992	0,000
4	0,6	0,6	0,229	0,93	0,93	0,029	0,993	0,993	0,000
5	0,8	0,8	0,081	0,94	0,94	0,020	0,994	0,994	0,000
6	1,0	1,0	0,000	0,95	0,95	0,016	0,995	0,995	0,000
7	1,2	1,2	- 0,063	0,96	0,96	0,012	0,996	0,996	0,000
8	1,4	1,4	- 0,109	0,97	0,97	0,009	0,997	0,997	0,000
9	16	16	- 0,144	0,98	0,98	0,005	0,998	0,998	0,000
10	1,8	1,8	- 0,172	0,99	0,99	0,001	0,999	0,999	0,000
11	2,0	2,0	- 0,195	1,00	1,00	0,000	1,000	1,000	0,000
12				1,10	1,10	- 0,035	1,010	1,010	0,000

Wykres zależności napięcia wyjściowegomostka wychyłowego od stosunku rezystancji Rx/Ro w zakresie 0 ÷ 2 [kΩ] przy założeniu, że R2=R3=R4=100Ω.

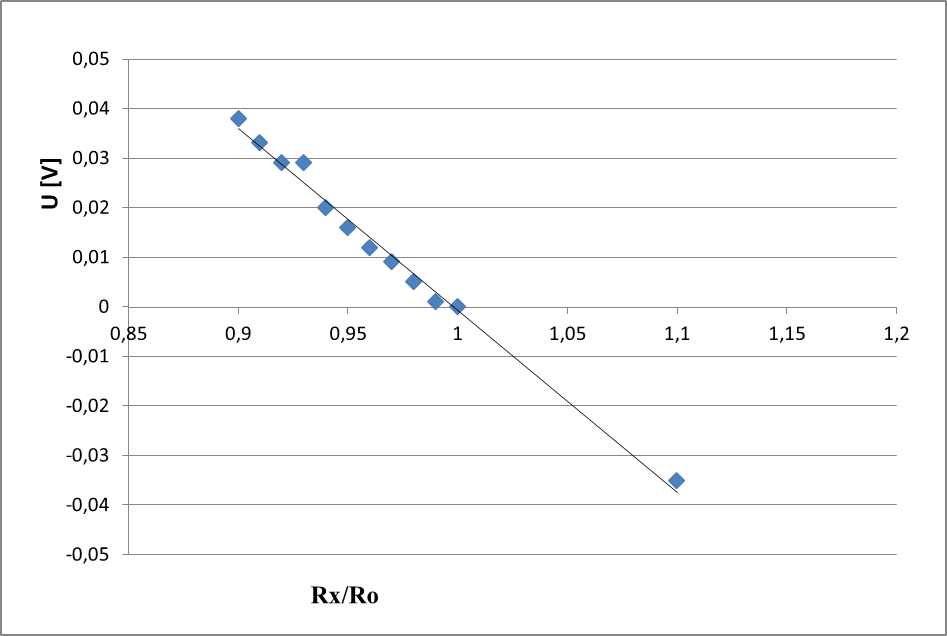
Wykres zależności napięcia wyjściowegomostka wychyłowego od stosunku rezystancji Rx/Ro w zakresie 0,9 ÷ 1,1 [kΩ] przy założeniu, że R2=R3=R4=100Ω.

Wykres zależności napięcia wyjściowegomostka wychyłowego od stosunku rezystancji Rx/Ro w zakresie 0,99 ÷ 1,01 [kΩ] przy założeniu, że R2=R3=R4=100Ω.

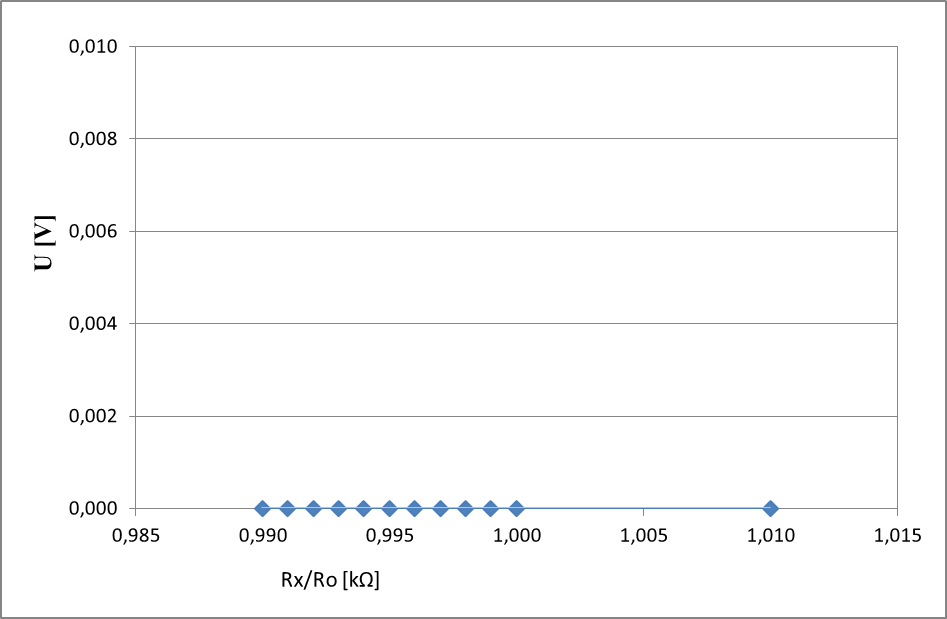
Wnioski:

Pierwszym ćwiczeniem, jakie wykonaliśmy, było sprawdzenie napięcia regulowanego źródła napięcia. Mogliśmy tutaj dokładnie zauważyć, jak brakuje nam czulszego woltomierza lub dodatkowego ziarna regulacji rezystora, które pozwoliłyby nam na dokonanie dokładniejszych pomiarów.

W drugim cwiczeniu postanowiliśmy sprawdzić jak zmieni się wynik pomiaru, jeżeli za R₃ i R₄ przyjmiemy takie wartości, by ich stosunek był nie 1 lecz 0,1. W tej sytuacji mieliśmy możliwość uzyskania na dekadzie jednego ziarna regulacji więcej (co zwiększa czułość). Zgodnie z przypuszczeniami wynik pomiaru okazał się dokładniejszy: dla
=1.

---