Zadanie 5.1

Dane:

X - zmienna losowa liczby wkrętów w pudełeczku

EX = 200 sztuk, wartość oczekiwana zmiennej X

sztuk, odchylenie standardowe w jednym opakowaniu

Szukane:

EY - wartość oczekiwana dla 100 opakowań wkrętów

- odchylenie standardowe dla 100 opakowań wkrętów

- współczynnik zmienności dla jednego opakowania

- współczynnik zmienności dla 100 opakowań

Obliczenia:

Y=100X

EY = E(100X)

ponieważ E(aZ) = aEZ więc:

EY = 100EX = 100*200 = 20000

Aby obliczyć
potrzebna jest wariancja zmiennej Y:

VY = V(100X)

ponieważ V(aZ) = a²VZ więc:

VY = 100²VX

VX =
= 7,84

VY = 10000*7,84 = 78400

Zadanie 5.2

Szukane:

Momenty zwyczajne, centralne pierwszego i drugiego rzędu

Moment zmiennej losowej X rzędu k:

Moment zwyczajny zmiennej losowej (X, Y) typu ciągłego rzędu „k+l”:

Momenty zwyczajne pierwszego rzędu, to takie, dla których suma k i l równa się 1:

Ponieważ funkcja f(x)=x+y jest symetryczna, zatem:

Momenty zwyczajne drugiego rzędu, to takie, dla których suma k i l równa się 2:

Moment, dla którego k=1 oraz l=1 nazywamy momentem mieszanym.

Momenty centralne zmiennej losowej (X, Y) rzędu „k+l”:

Analogicznie jak momenty zwyczajne k-tego rzędu definiuje się momenty centralne k-tego rzędu.

W rozwiązaniu korzystamy z własności wartości oczekiwanej.

W rozwiązaniu korzystamy z faktu, iż moment zwyczajny k-tego rzędu jest wartością oczekiwaną k-tej potęgi.

Zadanie 5.3

Dane:

Gęstość rozkładu normalnego to
.

Szukane:

Znaleźć x_p z równania F(x_p) = p, dla p = 0,1 ; 0,25 ; 0,5 ; 0,75 ; 0,9 ; 0,95 ;

Zauważamy, że F(-x) = 1-F(x)

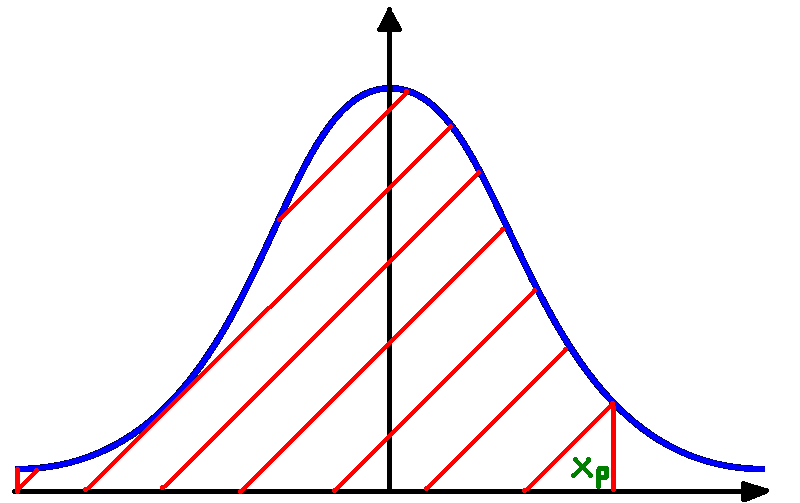
Korzystając z wartości III tablicy rozkładu normalnego odczytujemy wartości:

X_0,9 ≈ 1,28 ⇒ X_0,1 ≈ -1,28

X_0,75 ≈ 0,67 ⇒ X_0,25 ≈ -0,67

X_0,9 ≈ 0,5 ( wykres jest symetryczny )

X_0,95 ≈ 1,64

Zadanie 5.4

Dane:

P(X=0) = 1/5

P(X=1) = 4/5

Szukane:

Wykazać, że medianą jest punkt x=1. Narysować wykres P(X < x)

Wiemy, że zmienna losowa X jest typu skokowego, a zatem korzystając z twierdzenia o dystrybuancie takiej zmiennej mamy:

0 x
0

F(x) = 1/5 0 < x
1

1 x > 1

Wykres dystrybuanty:

y

1/5

x

1

Liczbę
nazywamy kwantylem p-tego rzędu 0<p<1, gdy spełni on warunki:

P(X

)
p

P(X

)
1-p

Kwanty rzędu p=0.5 nazywamy medianą.

Wykażemy, że x=1 jest medianą zmiennej losowej X:

P(X
1)
0.5 P(X<1) + P(X=1)
0.5 F(0)+F(1)
0.5

P(X
1)
1-0.5 1-P(X<1)
0.5 1-F(1)
0.5

4/5 + 1/5
0.5 1
0.5

1-1/5
0.5 0.8
0.5

Warunki na medianę zostały spełnione a zatem wykazaliśmy, że x=1 jest medianą.

Zadanie 5.5

Aby obliczyć medianę zmiennej losowej X potrzebna jest dystrybuanta. Ponieważ zmienna losowa jest ciągła, więc dystrybuanta ma postać:

, gdzie f(t) jest to funkcja gęstości zmiennej losowej X i w tym przypadku wynosi:

szukamy mediany, czyli miejsca, środka rozkładu x_0,5

F(x_0,5) = 0,5

sin x_0,5 = 0,5

x_0,5 = arcsinx_0,5 =

Zadanie 5.6

Dane:

Zmienna losowa może przyjmować 3 wartości : x1 = -1, x2 = 0, x3 = 1 z prawdopodobieństwami P(X=-1) = P(X=0) = ¼ P(X=1) = ½

Szukane:

Wyznaczyć dystrybuantę tego rozkładu, wykazać że każda wartość x z przedziału [0 ; 1]

jest medianą.

P( X ≤ -1 ) = 0 Dystrybuanta tego układu :

P( X ≤ 0 ) = ¼

P( X ≤ 1 ) = ½

W przedziale x ∈ [0 ; 1]

P( X ≤ 0 ) = P( X = -1 ) + P ( X = 0 ) = ½

P( X ≥ 1 ) = 1 - P( X < 1 ) = 1 - ½ = ½

Warunek na medianę: ( p - kwantyl p-tego rzędu )

P( X ≤ x ) ≥ p

P( X ≥ x ) ≤ 1 - p

Dla przedziału x ∈ [0 ; 1]

P( X ≥ 0 ) = ¼ + ½ = ¾ ≥ 1-p = 1- ½ = ½ ≥ ½ ⇒ ¾ ≥ ¼

P( X ≤ 1 ) = ¼ + ¼ + ½ = 1 ≥ 1 - p = ½

Zadanie 5.7

Ponieważ zmienna losowa ma rozkład jednostajny funkcja charakterystyczna jest określona wzorem:
. Jest to przekształcenie Fouriera funkcji f(x).

gdzie a, b
R; a < b

Zadanie 5.8

Dane:

Założenie ( lemat )

1. Dowód dla rozkładu dyskretnego:

2. Dowód dla rozkładu ciągłego:

Zadanie 5.9

Dane:

- funkcja gęstości

Szukane:

Rozkład, którego
byłaby funkcją charakterystyczną.

Jeżeli funkcja charakterystyczna
jest absolutnie całkowalna na prostej tzn:

to odpowiadająca jej zmienna losowa ma gęstość, którą wyznacza się ze wzoru:

Sprawdzamy zatem, czy spełniony jest warunek absolutnej całkowalności, czyli:

Ponieważ 2<
zatem warunek ten jest spełniony.

Wyznaczamy zatem gęstość odpowiadającą danej funkcji charakterystycznej:

Czyli:

f(x)=

Zatem funkcja f(x) jest funkcją gęstości prawdopodobieństwa jakiegoś rozkładu. Rozkładem tym jest rozkład Cauchy'ego, ponieważ f(x) jest jego funkcją gęstości.

-x_0,9=x_0,1

x_0,9

1

½

¼

1

0

-1

---