Sprawozdania:

1). Sprawozdanie pisane ręcznie prezentujemy wyłącznie na papierze podaniowym,

2). Sprawozdanie powinno składać się z :

- tabelki umieszczonej na pierwszej stronie w której umieszczone są następujące informacje: nazwa grupy, imiona i nazwiska osób wchodzących w skład zespołu wykonującego ćwiczenie oraz tytuł ćwiczenia,

- krótkiego wstępu teoretycznego, który powinien zawierać cel ćwiczenia, krótki opis zastosowanej w doświadczeniu metody pomiarowej, definicje (wraz z jednostkami) wielkości mierzonych,

- odpowiednich tabel, w które będą wpisywane mierzone wielkości fizyczne,

- wszystkie wykonywane obliczenia,

- wyraźnie oznaczony wynik pomiaru (wraz z policzonym błędem pomiaru oraz jednostką wielkości mierzonej),

- wnioski dotyczące metody pomiarowej użytej w doświadczeniu.

3). Sprawozdania powinny być oddawane na bieżąco.

Wykonanie wykresów

Przy sporządzaniu wykresu należy przestrzegać następujących zasad:

1. Osie układu, w którym sporządza się wykres powinny mieć w przybliżeniu jednakowej długości.

2. Na osi odciętych (x) odkłada się zawsze zmienną niezależna (parametr, który zmienia eksperymentator), a na osi rzędnych (y) zmienna zależną.

3. Osie powinny być opisane, tzn. w pobliżu końca osi po lewej stronie osi rzędnych i pod osią odciętych powinny być umieszczone symbole odkładanych wielkości fizycznych oraz w nawiasie kwadratowym, symbole jednostek w jakich te wielkości są wyrażone.

4. Na obydwu osiach powinny być naniesione skale w postaci kilku kresek opisanych liczbami „okrągłymi”.

5. Punkty doświadczalne muszą być wyraźnie zaznaczone, a jeśli oszacowane są błędy pomiarowe, to należy je nanieść w postaci pionowych odcinków.

6. Krzywa powinna być gładka i przebiegać tak, aby liczba punktów pomiarowych leżących pod nią i nad nią była prawie równa

Teoria błędów

Maksymalny błąd przypadkowy pojedynczego pomiaru bezpośredniego

- Pomiar długości - maksymalny błąd pomiaru długości zależy od użytego narzędzia pomiarowego.

W przypadku posługiwania się przymiarem (linijka, taśma miernicza) z podziałką co 1cm błąd pomiaru

ocenia się na 0,5cm. Gdy podziałka jest milimetrowa błąd jest równy najmniejszej podziałce - czyli

1mm. Błąd pomiaru przy użyciu suwmiarki, w zależności od jej wykonania szacuje się na 0,1mm, zaś

przy użyciu śruby mikrometrycznej, na 0,01mm.

- Pomiar masy - w przypadku pomiaru masy przy użyciu wagi technicznej, przyjmuje się, że

maksymalny błąd jest równy masie najmniejszego użytego przy ważeniu odważnika.

- Pomiar czasu - Przy pomiarze czasu za pomocą ręcznego sekundomierza (stopera), zwykle przyjmuje się, że błąd pomiaru nie przekracza 0,2s.

- Pomiar temperatury - Przyjmuje się, ze dokładność pomiaru temperatury przy użyciu termometrów

cieczowych odpowiada jednej podziałce - przeważnie jest to 1mm.

W przypadku pomiaru dowolnej wielkości za pomocą mierników cyfrowych, jeśli producent nie określił dokładności przyrządu, przyjmuje się, ze błąd nie przekracza wartości określonej cyfrą 5 na miejscu po ostatnim miejscu wyświetlanym. Np. gdy miernik wskazuje wartość 1,25 jednostki, to należy przyjąć, ze błąd nie przekracza 0,005 tejże jednostki.

Ocena dokładności średniej arytmetycznej wyników pomiarów

Aby zmniejszyć wpływ błędów przypadkowych na wynik pomiaru często dokonuje się w ustalonych warunkach serii pomiarów x₁, x₂, x₃, …, x_n wartości danej wielkości, i oblicza się wartość średnią :

Do oceny błędu uzyskanej wartości używa się często błędu średniego średniej arytmetycznej.

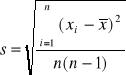
Zaokrąglanie liczb. Często zdarza się tak, że liczbę będącą wynikiem działań na liczbach przybliżonych należy zaokrąglić. Stosuje się wówczas następujące zasady:

a). Jeżeli pierwsza z odrzucanych cyfr jest większa niż 5, to ostatnią pozostającą cyfrę liczby należy zwiększyć o jeden np. zaokrąglając liczbę 1,357 do trzech cyfr znaczących należy napisać 2,36, zaś do dwu cyfr znaczących 2,4 - analogicznie z liczbą 3468, zaokrąglając do trzech cyfr znaczących należy napisać 3,47*10³, czyli 3470

b). Jeżeli pierwsza z odrzucanych cyfr jest mniejsza niż 5, to ostatnią pozostającą cyfrę zachowuje się cez zmiany np. 3,531 zaokrąglając do trzech cyfr znaczących należy napisać 3,53 - analogicznie 9642 - 9,64*10³, czyli 9640

c). Jeżeli jedyną odrzucaną cyfrą jest 5, to ostatnią pozostającą cyfrę, liczby w przypadku gdy jest ona parzysta, zachowuje się bez zmiany, zaś gdy jest nieparzysta, zwiększa się o jeden np. zaokrąglając liczbę 9,225 do trzech cyfr znaczących należy napisać 9,22 - analogicznie 2,235 - 2,24.

Dodawanie i odejmowanie liczb przybliżonych. Wyniki dodawania lub odejmowania liczb o różnej dokładności należy zapisywać z taką dokładnością, jaką ma liczba najmniej dokładna.

Np. w rezultacie sumowania liczb 45,21+0,5312+4,721 otrzymamy 50,4622. Ponieważ pierwszy składnik sumy 45,21 jest najmniej dokładny, wynik sumowania należy zaokrąglić do tego samego rzędu, czyli do dwóch miejsc po przecinku. Zatem należy zapisać 45,21+0,5312+4,721 = 50,46

Mnożenie i dzielenie liczb przybliżonych. Jeśli dokonuje się mnożenie (lub dzielenie) liczby zawierającej m cyfr znaczących przez liczbę zawierającą n cyfr znaczących, to iloczyn (iloraz) należy zaokrąglić, aby zawierał m cyfr znaczących gdy m<n, albo n cyfr znaczących gdy n<m.

Np. w rezultacie mnożenia liczb 3,235 przez 2,3 otrzymamy 7,4405. Ponieważ mnożna zawiera cztery, a mnożnik dwie cyfry znaczące, to iloczyn powinien zawierać dwie cyfry znaczące, a zatem należy napisać że3,235*2,3=7,4

Sposób zapisywania wyników pomiarów i obliczeń

Po dokonaniu oceny błędu, niezależnie od tego czy jest to maksymalny błąd przypadkowy pojedynczego pomiary, średni błąd średniej arytmetycznej, zawsze należy zaokrąglić uzyskany wynik do jednej, a co najwyżej dwu cyfr znaczących. Wynik pomiarów lub obliczeń należy tak zaokrąglić, aby rząd jego ostatniej cyfry znaczącej był taki sam, jak rząd ostatniej cyfry znaczącej oszacowanego błędu.

Np. Po dokonaniu pomiarów czasu t przebiegu pewnego zjawiska obliczono średni czas t_śr=18,413s i średni błąd wartości średniej s=0,0478s. Wynik obliczeń po zaokrągleniach należy zapisać jako :

t = (18,41±0,05) [s].

---