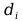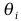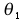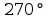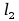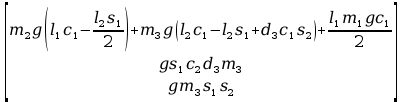Akademia Techniczno – Humanistyczna w Bielsku – Białej Bielsko – Biała,17.01.2016
Wydział Budowy Maszyn i Informatyki
Automatyka i Robotyka/Mechatronika i Robotyka
Rok akademicki: 2015/2016
Rok studiów: 3
Semestr: 5
PROJEKT
 Z
DYNAMIKI MANIPULATORÓW
Z
DYNAMIKI MANIPULATORÓW
6
Jakub Koziołek
Wojciech Grzybek
Wstęp teoretyczny:
Przedstawiony tutaj projekt z dynamiki manipulatorów jest kompletnym rozwiązaniem prostego zadania dynamiki. Przedmiotem projektu jest przykładowy manipulator (robot). W pierwszej kolejności należy rozwiązać proste zadanie kinematyki zgodnie z metodą tradycyjną a następnie zgodnie z notacją Denavita – Hartenberga w celu sprawdzenia.
Proste zadanie dynamiki
W zadaniu prostym
dynamiki dany jest punkt trajektorii ruchu, prędkości i
przyśpieszenia, a wyznacza się wektory sił i momentów napędowych
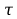 .
W celu prawidłowego wykonania zadania należy wyznaczyć macierze
transformacji. By tego dokonać, stosuje się dwie metody:
.
W celu prawidłowego wykonania zadania należy wyznaczyć macierze
transformacji. By tego dokonać, stosuje się dwie metody:
metoda tradycyjna
Należy w tym celu wyznaczyć macierze rotacji, które są w następującej postaci:


Należy również wyznaczyć na podstawie przyjętych układów współrzędnych, wektor położenia początkowego układów:
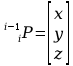

Macierz transformacji otrzymuje się następująco:



metoda algorytmu Denavita – Hartenberga
Metoda ta polega na konstrukcji tabeli parametrów Denavita – Hartenberga i stworzeniu macierzy transformacji na podstawie otrzymanych wyników. Tebela wygląda następująco:
|
i |
|
|
|
|
|
|
|
|
|
|


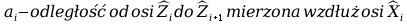


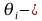


Algorytm przywiązywania układów współrzędnych do członu:
1) Zidentyfikowanie osi połączeń (i oraz i+1)
2) Znalezienie prostej obustronnie prostopadłej do nich lub punktu ich przecięcia. Przyjęcie początku układu współrzędnych członu w punkcie przecięcia i –tej osi z prostą obustronnie prostopadłą lub punkcie przecięcia osi i oraz i+1
3)
Przyjęcie osi
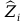 w osi i-tego
połączenia
w osi i-tego
połączenia
4)
Przyjęcie osi
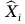 wzdłuż prostej obustronnie prostopadłej lub jeśli osie przecinają
się przyjęcie
wzdłuż prostej obustronnie prostopadłej lub jeśli osie przecinają
się przyjęcie
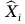 jako normalną do płaszczyzny zawierającej te dwie osie.
jako normalną do płaszczyzny zawierającej te dwie osie.
5)
Przyjęcie
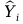 tak, aby uzupełniała prawoskrętny układ współrzędnych.
tak, aby uzupełniała prawoskrętny układ współrzędnych.
6)
Układ {0} pokrywa się z układem {1}, gdy zmienna pierwszego
połączenia jest równa zero. Należy przyjąć dowolne usytuowanie
początku układu {N} i zwrot osi
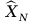 ,
tak aby spowodować zerowanie się możliwie największej liczby
parametrów.
,
tak aby spowodować zerowanie się możliwie największej liczby
parametrów.
Macierz transformacji:
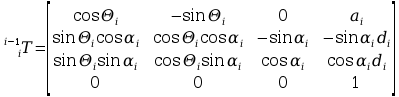
Schemat manipulatora wraz z przyjętymi układami współrzędnych według notacji
Denavita – Hartenberga:
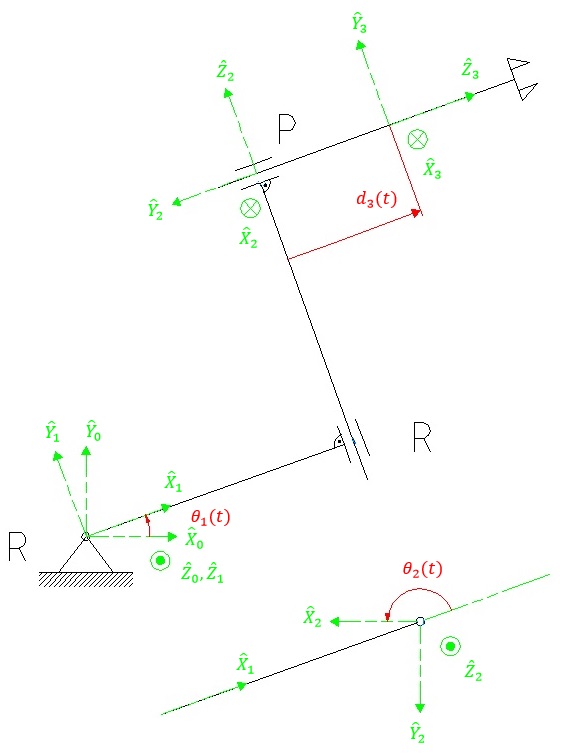
Sformułowanie wektora współrzędnych uogólnionych:
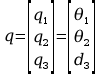
Tabela parametrów charakterystycznych:
|
i |
|
|
|
|
|
1 |
0 |
0 |
0 |
|
|
2 |
|
|
|
|
|
3 |
0 |
|
|
0 |
Macierze transformacji:
Wyznaczone metodą tradycyjną
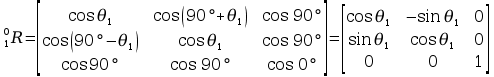



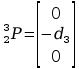

Wyznaczone metodą Denavita – Hartenberga
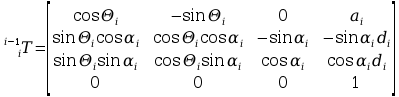
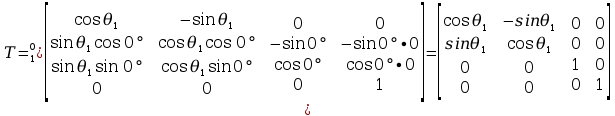
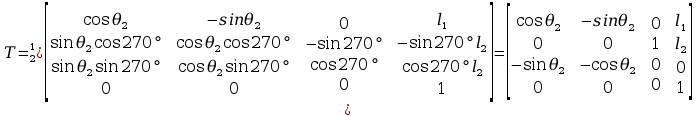
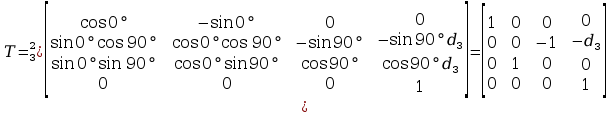
Uzyskanie
macierzy
 :
:
W celu uproszczenia zapisu kolejnych macierzy wprowadzono nowe oznaczenia:





 =
=
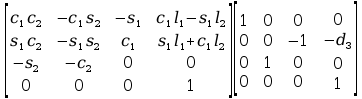 =
=
Wyznaczenie pochodnych cząstkowych:
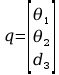
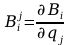
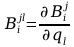


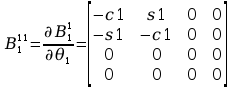

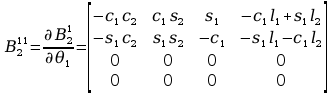
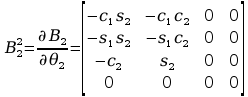
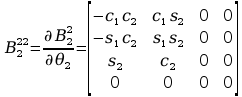
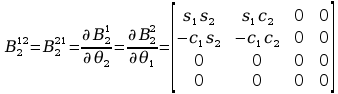
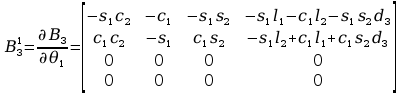


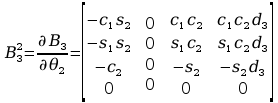
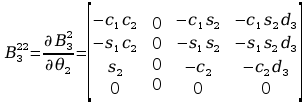
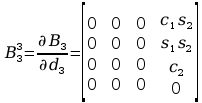
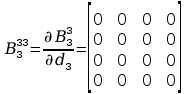

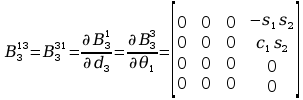

Wyznaczenie macierzy H:
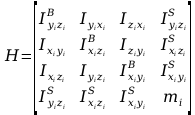
Momenty bezwładności względem płaszczyzn
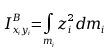
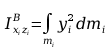

Momenty statyczne względem płaszczyzn

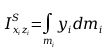
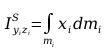
Momenty odśrodkowe
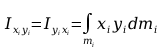


Obliczanie macierzy H1:
Momenty bezwładności
względem płaszczyzn
Rozkład masy tylko na osi x1
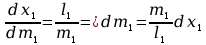
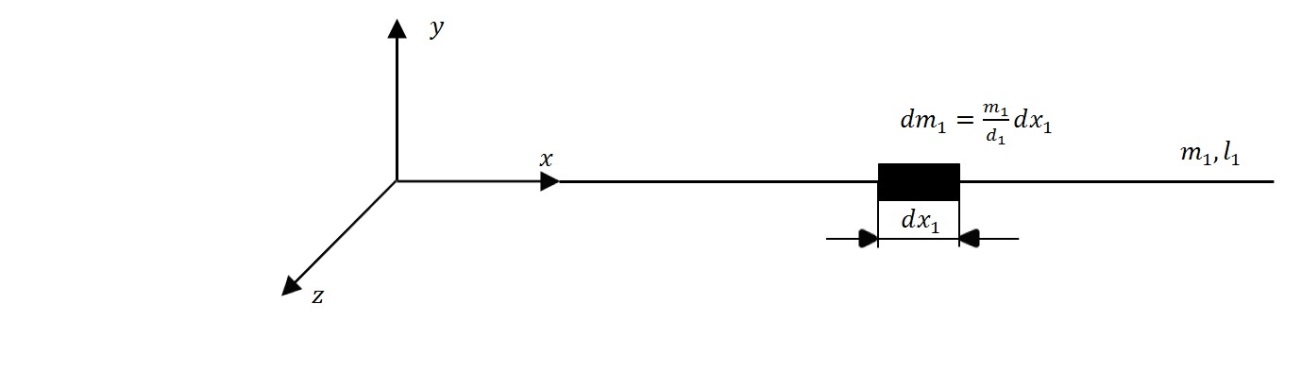
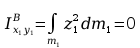


Momenty odśrodkowe
Momenty
odśrodkowe występują jedynie gdy masa jest rozłożona po co
najmniej dwóch osiach, zatem w tym przypadku wszystkie będą równe
0.
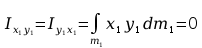
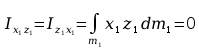
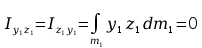
Momenty statyczne względem płaszczyzn
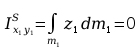
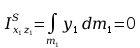
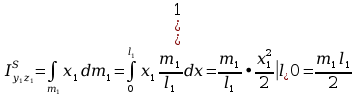

Obliczanie macierzy H2:
Momenty bezwładności względem płaszczyzn
Rozkład masy tylko na osi z2


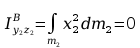

Momenty odśrodkowe
Momenty
odśrodkowe występują jedynie gdy masa jest rozłożona po co
najmniej dwóch osiach, zatem w tym przypadku wszystkie będą równe
0.
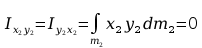

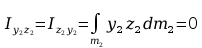
Momenty statyczne względem płaszczyzn
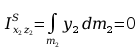
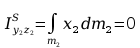
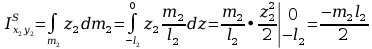
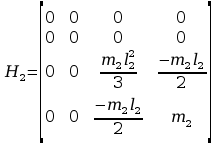
Obliczanie macierzy H3:
Momenty bezwładności
względem płaszczyzn
Rozkład masy tylko na osi z3
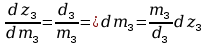
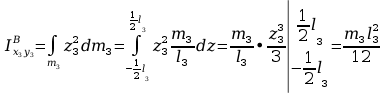


Momenty odśrodkowe
Momenty
odśrodkowe występują jedynie gdy masa jest rozłożona po co
najmniej dwóch osiach, zatem w tym przypadku wszystkie będą równe
0.
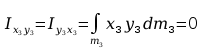

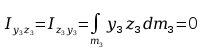
Momenty statyczne względem płaszczyzn
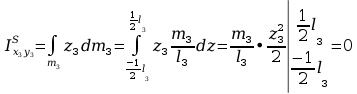

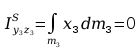
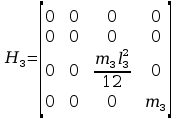
Obliczenia macierzy A:
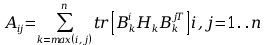




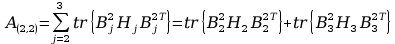


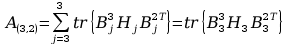
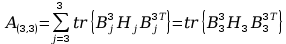
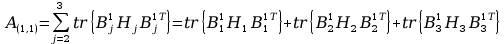
 +
+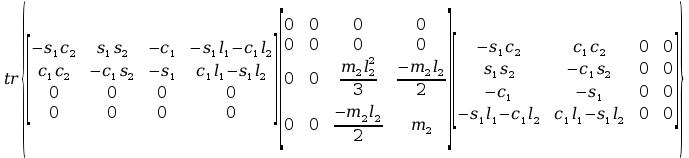
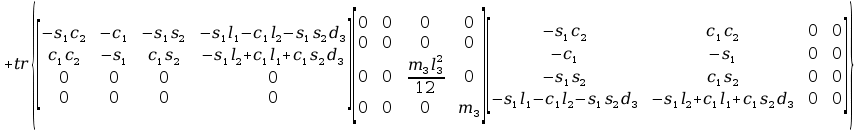
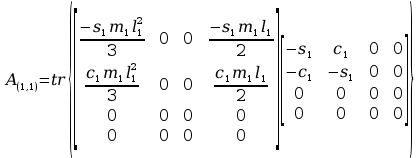
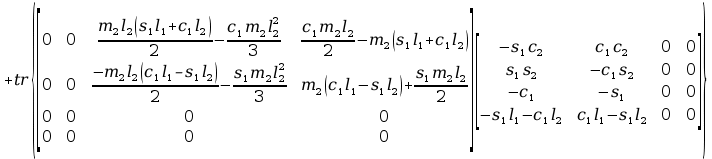
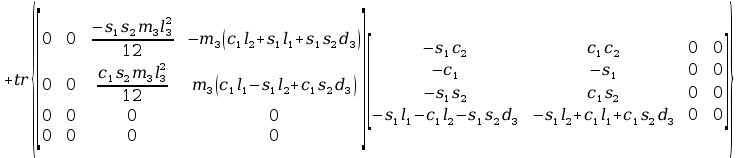
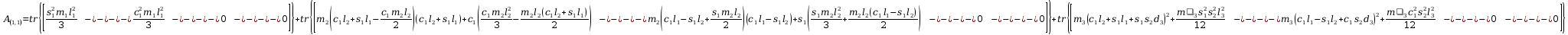


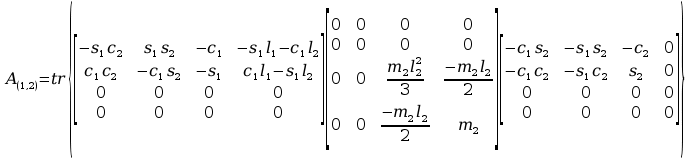
+
 +
+
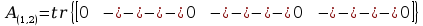 +
+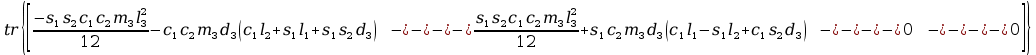


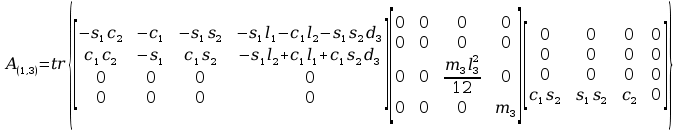
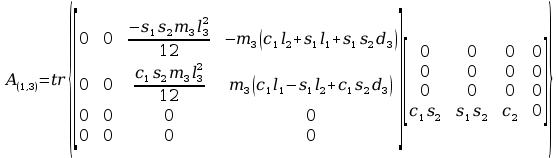



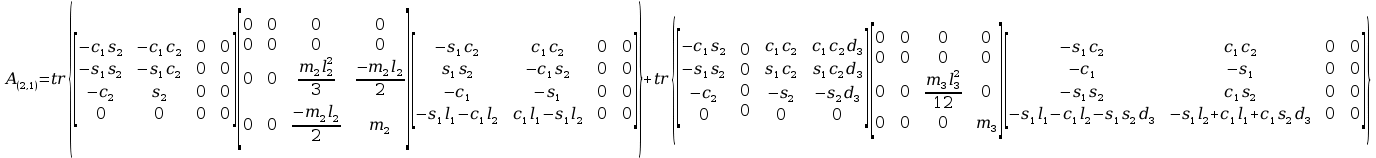
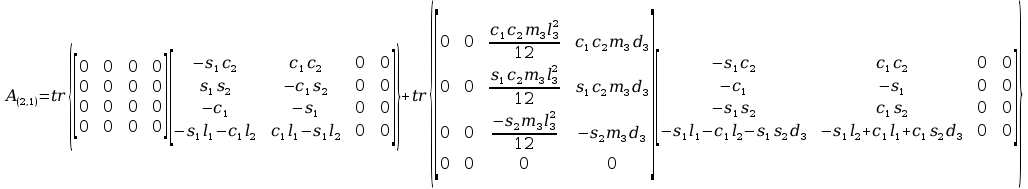
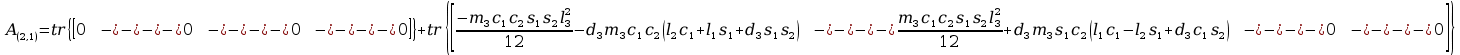

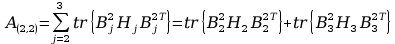
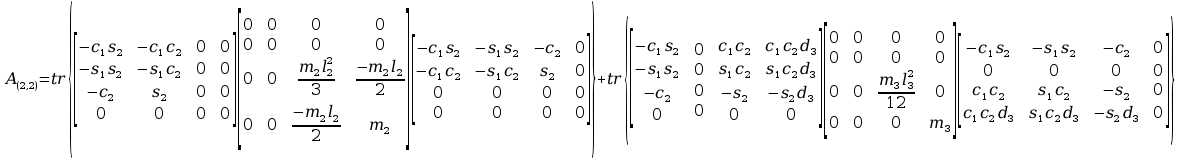
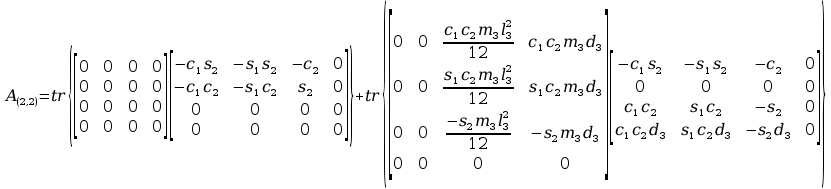

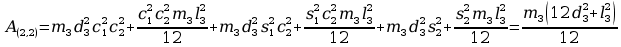


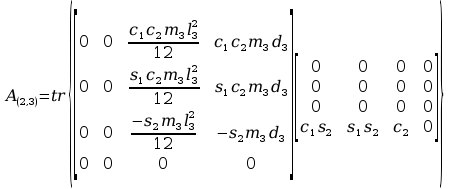




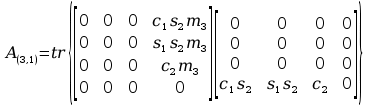


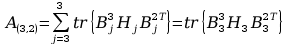
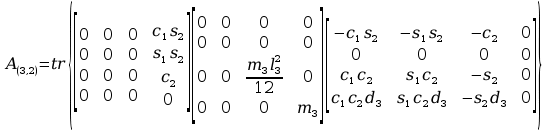



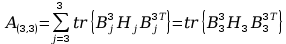

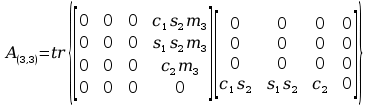
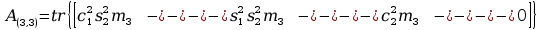
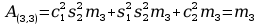
11. Wyznaczanie Macierzy C.
Aby przejść do wyznaczania powyższych macierzy A musimy zająć się transponowaniem macierzy pochodnej cząstkowej B, bo jak zobaczymy w rozpisanych j wzorach są one nam potrzebne, tak więc :
 =
=

 =
=

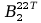 =
=

 =
=
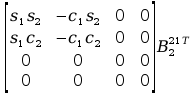 =
=
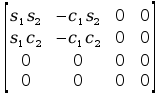
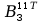 =
=

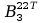 =
=
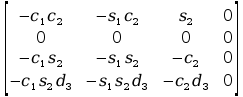
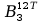 =
=
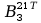 =
=

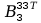 =
=
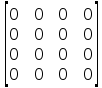
 =
=
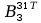 =
=
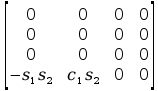

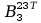 =
=
 =
=
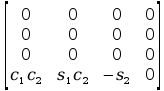

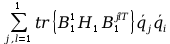 +
+
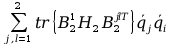 +
+
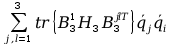 =
=
=
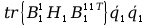 +
+
 +
+
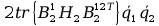 + tr
+ tr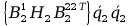 +
+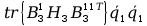 +
+
+2tr
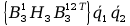 +
+
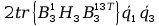 +tr
+tr
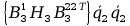 +2tr
+2tr
 +
+
 =
=
=
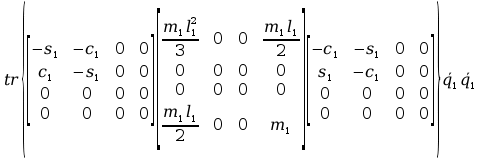 +
+
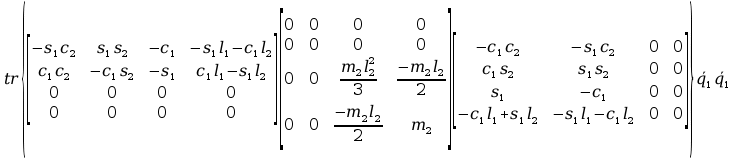 +
+
+
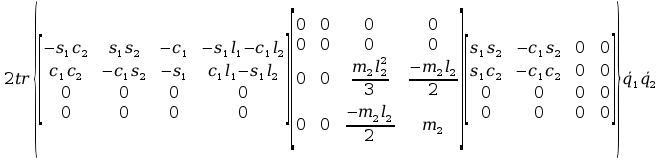 + tr
+ tr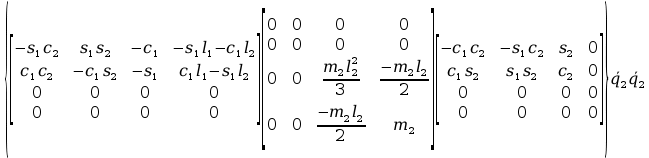 +
+
+
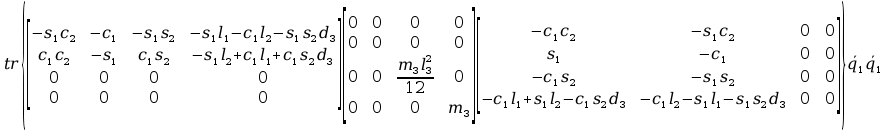 +
+
+
2tr
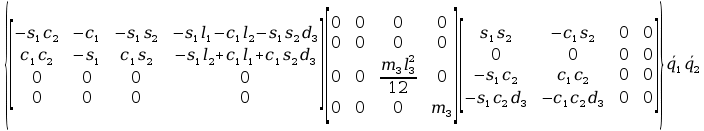 +
+
+
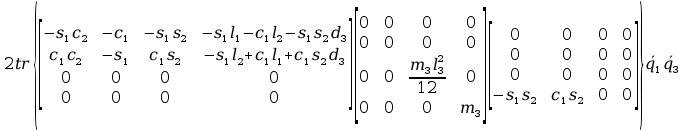 +
+
+
tr
 +
+
+
2tr
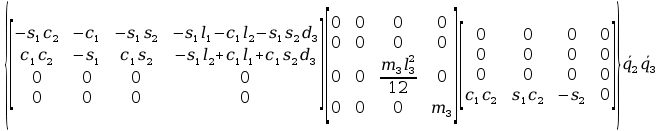 +
+
+
 =
=
=
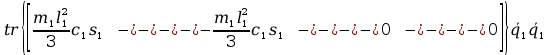 +
+
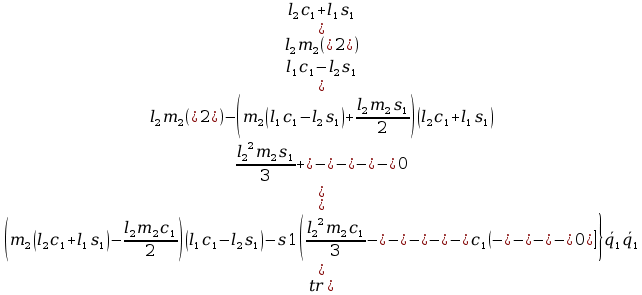 +
+
+
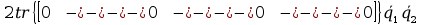 + tr
+ tr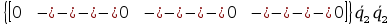 +
+
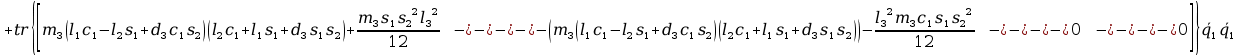
+
2tr
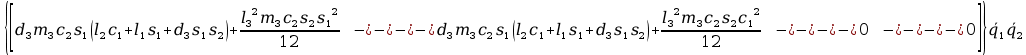 +
+
+
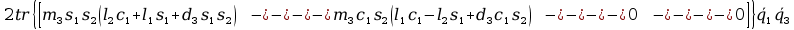 +
+
+
tr
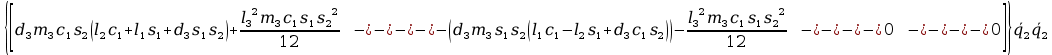 +
+
+
2tr
 +
+
 =
=
=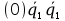 +
+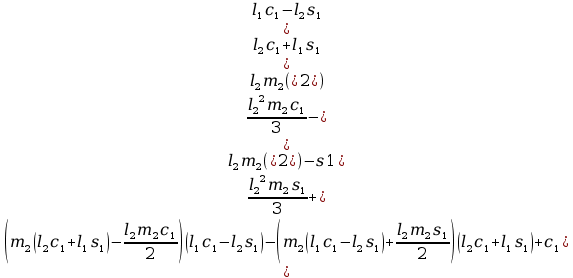 +
+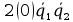 +
+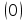
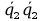 +
+
 + 2
+ 2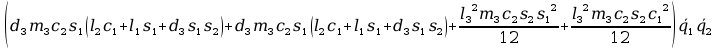 +
+
+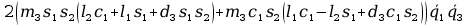 +
+

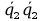 +
+
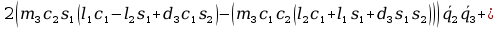
 =
=
=
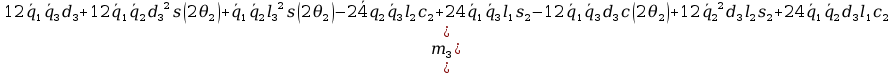

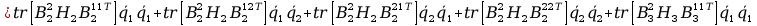

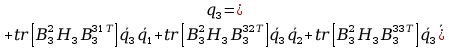

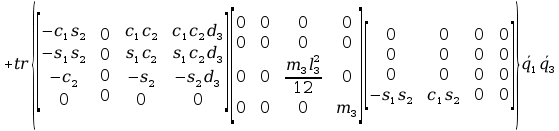
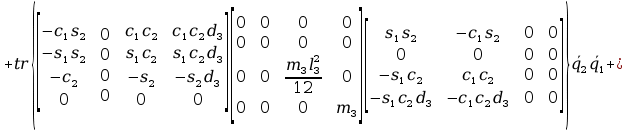
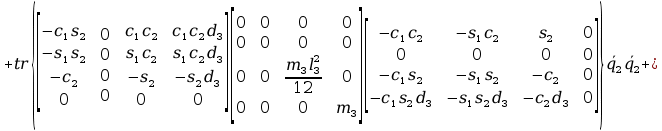
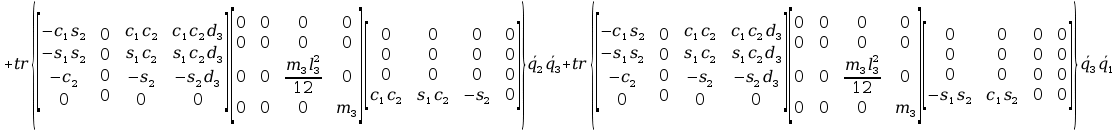


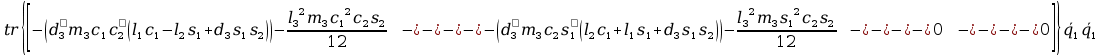
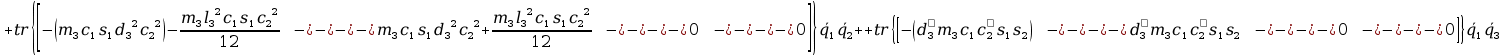
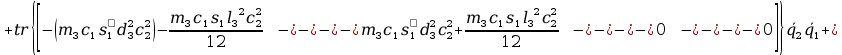


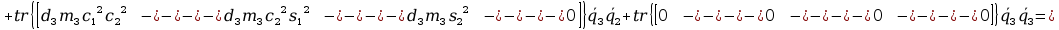
 +
+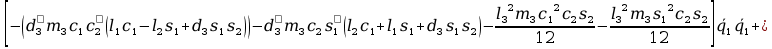
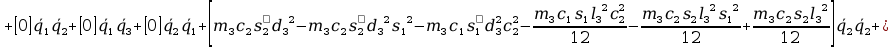
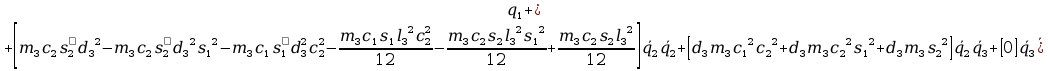

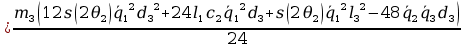
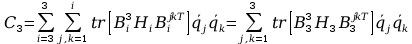

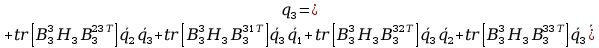
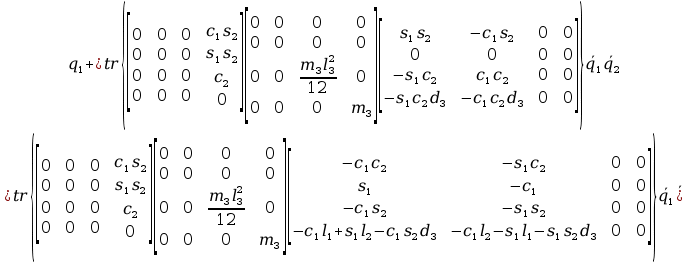



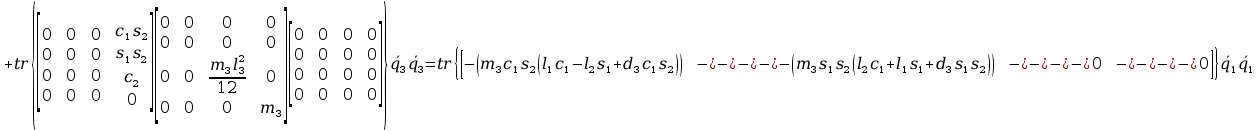
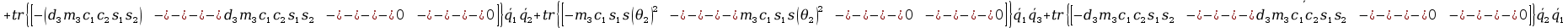
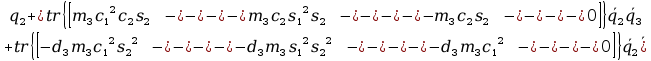
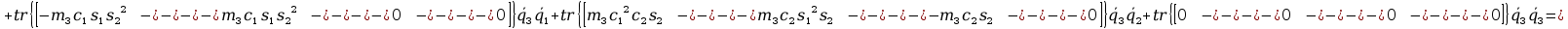
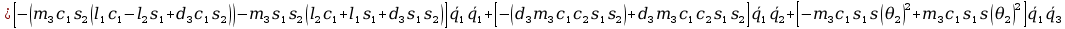
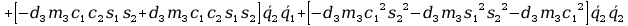
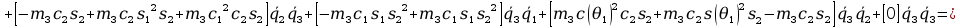
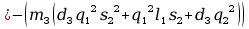
12. Wyznaczanie Macierzy G.
Macierz
 :
:  =
=

Macierze środków ciężkości :
 =
=

 =
=
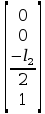
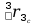 =
=
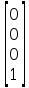
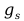 =
=
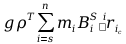
 =
=
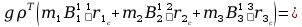
=
g
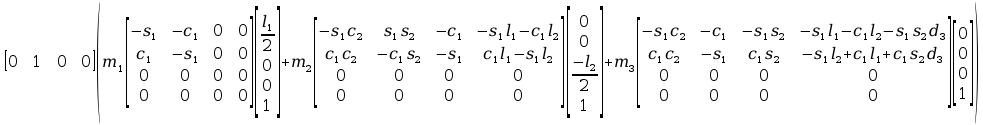 =
=
=
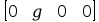
 =
=
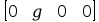
 =
=
=
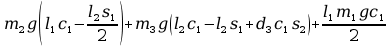
 =
=
 =
=
=
g
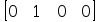
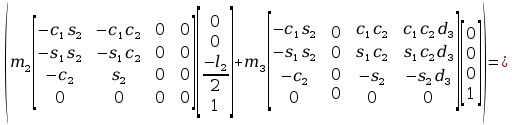
=
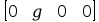
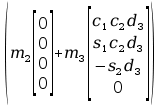 =
=
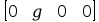
 =
=
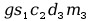
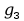 =
=
 =
g
=
g
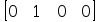
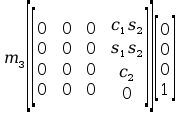 =
=
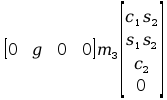 =
=
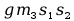
Wszystkie wartości G przedstawione w postaci macierzy 3x1 (ostateczny wygląd macierzy G) :
Podsumowanie – podstawienie obliczonych wartości rachunku macierzowego równań ruchu.
Postać ogólna równań ruchu:
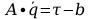
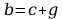
Postać szczególna równań ruchu dla manipulatora 3-członowego:
 =
=
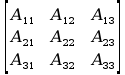


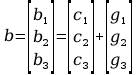

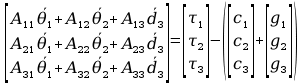

Wyszukiwarka
Podobne podstrony:
sprawozdanie na gotowo kruszarki dev, pliki od was
Projekt na informatykę
Kawerny solne – magazynowanie gazu Gazownictwo projekt na 5
Obserwacja na gotowo
projek na cw
Projekt na informatykę 2
Projekt na protezę kosmetyczną ramienia
Egzamin Tektonika na gotowo
Projekt na Zarządzanie Procesami
projekt na itr
Projekt na zaliczenie
Projekt na ocene mój
Projekt na kółko teatralne dla dzieci z klas I
GRUPA LOTOS S projekt na szzl
projekt na podstawie zakładu kosmetycznego (8 str), Ekonomia
Projekt na mikrosocjologię - monografia, Praca licencjacka
projekt na el en wykresy i scre Nieznany
więcej podobnych podstron