Teoria sygnałów, laboratorium - ćwiczenie 5

Przykładowe pytania z zakresu piątego ćwiczenia:

Zalecana literatura to:

[2] - ćw. 5 - rozdz. 1.4, 1.5, 1.6;

ćw. 6 rozdz. 4.1;

[5] - rozdz. 3.6, 3.11, 3.13 (głównie wstęp i 3.13.1, ale pozostałe części też są wartościowe), 3.14 i 3.15.

Wszystkie pytanie, o ile wyraźnie nie zaznaczono, że jest inaczej, dotyczą Dyskretnej Transformacji Fouriera.

Wszystkie rozważane ciągi pierwotne i ciągi transformat należy umieć opisać wzorem, wykreślić na kartce oraz z użyciem pakietu Matlab.

1. Korzystając ze wzoru na DFT wyznacz transformatę N-elementowego ciągu, będącego fragmentem ciągu delty Kroneckera (dla n od zera do N-1).

2. Korzystając ze wzoru na DFT wyznacz transformatę N-elementowego ciągu, będącego fragmentem ciągu delty Kroneckera (dla n od zera do N-1) opóźnionej o k indeksów.

3. W jaki sposób należałoby zinterpretować wyznaczanie transformaty DFT dla delty Kroneckera „przyspieszonej” o k indeksów? (pobierając N próbek dla n od zera do N-1 nie uwzględnilibyśmy jedynej niezerowej wartości w ciągu delty)

4. W jaki sposób na podstawie znajomości transformaty delty Kroneckera przesuniętej o k indeksów i na podstawie podobieństwa wzorów na DFT oraz IDFT (odwrotną DFT) można „przewidzieć” ciąg pierwotny dla widma w postaci delty Kroneckera?

5. Korzystając ze wzoru na IDFT wyznaczyć ciąg pierwotny dla widma w postaci
   .

6. Korzystając ze wzoru na IDFT wyznaczyć ciąg pierwotny dla widma w postaci
   .

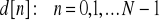
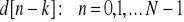
7. Korzystając ze wzoru na DFT wyznaczyć transformatę ciągu będącego sumą poprzesuwanych delt Kroneckera - np.: x[n] = d[n] + d[n-1] + d[n-2] lub x[n] = 0,5 d[n] - 0,25 d[n-1] + 0,125 d[n-2].

8. Wyznaczyć transformatę ciągu podobnego do określonego w punkcie 7 na podstawie znajomości widma d[n-k] (określonego ogólnie dla dowolnego k) i liniowości DFT.

9. Metodą analogiczną do a) punktu 7, b) punktu 8, wyznaczyć transformatę ciągu prostokątnego, zdefiniowanego np. jako 5 wartości „1” i następnie 27 wartości „0”.

10. Problem analogiczny do określonego w punkcie 9, jednak po odwróceniu ról ciągu pierwotnego i transformaty - zatem ciąg prostokątny stanowi widmo, natomiast poszukujemy dla niego ciągu pierwotnego (IDFT).

11. Korzystając ze znajomości ciągu pierwotnego dla transformaty w postaci d[n-k] (patrz punkty 4-6) wyznaczyć transformatę dla ciągu próbek kosinusoidy (sinusoidy) przy spełnionym warunku, iż w przedziale próbowania mieści się całkowita ilość okresów tej kosinusoidy (sinusoidy).

12. Wyjaśnić dlaczego współczynniki transformaty można potraktować jak współczynniki rozwinięcia ciągu pierwotnego w szereg złożony z odpowiednich ciągów bazowych:

1. dla ciągów bazowych w postaci próbkowanych sinusoid oraz kosinusoid;

2. dla ciągów bazowych w postaci próbkowanych funkcji
   .

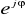
13. Jak można uzasadnić efekt „przecieku” polegający na tym, że transformata próbkowanej kosinusoidy (sinusoidy) może zawierać więcej niż dwa elementy niezerowe, mimo iż wiemy, że dla sygnałów i widm analogowych widmo kosinusoidy (lub sinusoidy) zawiera zawsze dokładnie dwie rozłożone symetrycznie delty Diraca? (Ważne pytanie !)

14. Jeżeli znane jest widmo dla danego ciągu pierwotnego N-elementowego, to co można powiedzieć o widmie ciągu otrzymanego przez wydłużenie tego ciągu o pewną ilość wartości zerowych:

1. gdy ilość elementów zerowych wynosi
   ;

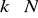
2. gdy dodano ilość elementów zerowych inną niż
   ?

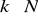
(oprócz przyjrzenia się wzorowi na DFT warto tu nawiązać do relacji między transformacjami DFT i D-TFT)

15. Jeżeli znane jest widmo dla danego ciągu pierwotnego N-elementowego, to co można powiedzieć o widmie ciągu
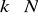
    -elementowego otrzymanego przez wstawienie pomiędzy kolejne elementy ciągu N-elementowego (k-1)-elementowych podciągów zerowych?

16. Jeżeli znane jest widmo dla danego ciągu pierwotnego N-elementowego, to co można powiedzieć o widmie ciągu o tej samej długości (N-elementowego) otrzymanego przez wyzerowanie podciągów pomiędzy co k-tą próbką? (sytuacja analogiczna do próbkowania związanego z twierdzeniem o próbkowaniu, tylko że tym razem próbkujemy ciąg a nie sygnał analogowy)

17. Przyjmując, że widmo DFT stanowi precyzyjną reprezentację widma D-TFT (mocno wyidealizowane założenie), opisać jak należy określić widmo DFT filtru, by za pomocą pomnożenia widm (filtru i sygnału) otrzymać dolnopasmową część sygnału? - Podać przykład takiego widma filtru.

18. Przyjmując, że widmo DFT stanowi precyzyjną reprezentację widma D-TFT (mocno wyidealizowane założenie), opisać jak należy określić widmo DFT filtru, by za pomocą pomnożenia widm (filtru i sygnału) otrzymać górnopasmową część sygnału? - Podać przykład takiego widma filtru.

19. Zademonstrować za pomocą pakietu Matlab, że oddzielenie części dolnopasmowej i górnopasmowej (stanowiącej uzupełnienie do części dolnopasmowej) sygnału w dziedzinie widma prowadzi do dwóch ciągów w dziedzinie pierwotnej(indeksów czasowych), które po dodaniu w dziedzinie indeksów czasowych dają kompletny ciąg sygnału.

20. Skąd bierze się część urojona w ciągu pierwotnym otrzymanym po zastosowaniu funkcji ifft Matlaba, mimo iż widmo spełnia odpowiednie warunki symetrii? Jak należy wówczas postąpić, by skorygować ten efekt?

21. Zademonstrować za pomocą pakietu Matlab, że filtracja filtrem z punktu 17 lub 18 prowadzi zwykle do filtracji „nieco” odbiegającej od dolno- lub górnopasmowej (tzn., że przyjęte założenie może zbytnio upraszczać problem).

Teoria sygnałów, laboratorium - ćwiczenie 5

1

---