Literatura:

Krysicki, ... - Statystyka matematyczna

Luszniewicz - Statystyka stosowana

Sobczyk - Statystyka

Podstawy rachunku prawdopodobieństwa

Prawdopodobieństwo zajścia zdarzenia A oznacza się ogólnie jako: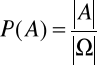
, 0≤P(A)≤1

Permutacja

Wariacja bez powtórzeń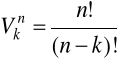

Wariacja z powtórzeniami

Kombinacja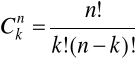

Prawdopodobieństwo całkowite

Prawdopodobieństwo warunkowe

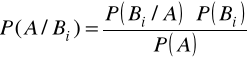
Zdarzenia niezależne

Schemat Bernoulliego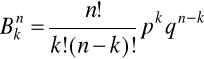
, gdzie p - prawdopodobieństwo sukcesu w 1-ej próbie, q - prawdopodobieństwo porażki w 1-ej próbie, n -liczba prób, k -liczba sukcesów.

STATYSTYKA MATEMATYCZNA

Statystyka matematyczna zajmuje się opisywaniem i analizą zjawisk masowych przy użyciu metod rachunku prawdopodobieństwa.

Populacja generalna - Ogół zbiorowości; założenie: przynajmniej jedna cecha wspólna

Jeśli badamy wszystkie elementy populacji generalnej to mamy do czynienia z badaniem kompletnym. Jeżeli mamy reprezentację danej populacji to mamy do czynienia z badaniem cząstkowym. Często badania kompletnego nie da się wykonać.

Próbka - stanowi reprezentację populacji. Częstości występowania w próbce każdej z badanych cech nie powinny się znacznie różnić od częstości występowania tych cech w populacji generalnej.

Próbka losowa prosta, n-elementowa - jest to próbka wylosowana z populacji w taki sposób, że przed jej pobraniem każdy podzbiór składający się z n elementów populacji generalnej ma takie samą szansę wylosowania.

Badaniu mogą podlegać cechy:

• mierzalne (ilościowe) - np. długość, ciężar;

• niemierzalne (jakościowe) - np. kolor, płeć, zawód (nadaje się im często wartości liczbowe - tzw. rangi).

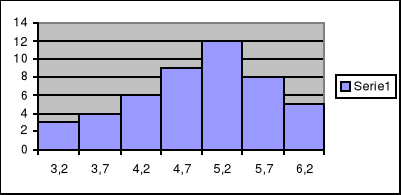
Szereg rozdzielczy (tworzenie histogramu)

Mamy n elementową próbę wyników, uszeregowanych w sposób rosnący (x₁...x_n)

1. Obliczamy rozstęp.
   

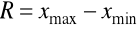
2. Wyznaczamy ilość klas.
   .

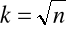
3. Wyznaczamy długość klasy.
   .

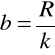
4. Znając dokładność pomiaru α (np. gdy wyniki są podane z dokładnością do jednego miejsca po przecinku to α=0,1) wyznaczamy dolną granicę pierwszej klasy
   .

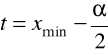
5. Dodając do początku każdej z klas długość klasy otrzymujemy poszczególne klasy. Wyniki, które mieszczą się w kolejnych przedziałach należą do kolejnych klas.

Np.:

Nr klasy	Klasy	Liczebności klas	Środki klas
1	2,95-3,45	3	3,2
2	3,45-3,95	4	3,7
3	3,95-4,45	6	4,2
4	4,45-4,95	9	4,7
5	4,95-5,45	12	5,2
6	5,45-5,95	8	5,7
7	5,95-6,45	5	6,2

Histogram (inaczej wykres słupkowy) to graficzne przedstawienie powyższej tabeli

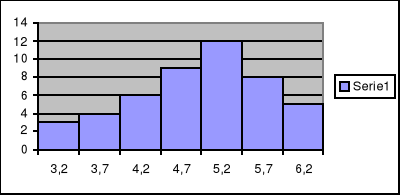
Podstawowe statystyki sumacyjne:

1. Estymatory wartości oczekiwanej

• średnia arytmetyczna
  ;

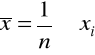
• mediana - wartość środkowa (przy uszeregowaniu wyników w sposób rosnący, jeżeli mamy parzystą liczbę wyników to dwie środkowe dzielimy przez 2);

• moda - najczęściej powtarzająca się wartość. Jeśli jest kilka wartości powtarzających się jednakowo często to mody nie ma. Modą nie może być ani wartość minimalna, ani maksymalna.

• średnia geometryczna
  ;

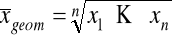
oraz

• kwartyl dolny - mediana z dolnej połowy (bierzemy połowę wyników i dodajemy medianę z całości i z tej grupy wyliczamy kolejną medianę)

• kwartyl górny - mediana z górnej połowy (bierzemy drugą połowę wyników i dodajemy medianę na początek. Z tej grupy wyliczamy kolejną medianę)

2. Miary rozproszenia

• wariancja (moment centralny rzędu 2-go)
  
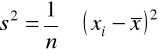
  . Dla małych prób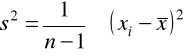
  .

• Odchylenie standardowe
  

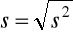
• Błąd standardowy
  

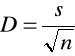
3. Miary asymetrii

• skośność
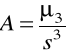
  , gdzie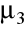
  to moment centralny rzędu 3-go;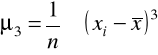
  . Służy do badania asymetrii (czy rozkład wyników jest symetryczny względem średniej. Im mniejsza wartość skośności tym rozkład bardziej symetryczny (ujemna skośność - to symetria ujemna, czyli więcej wyników większych od średniej, jeśli skośność dodatnia to na odwrót)

• kurtoza
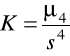
  . Bada spłaszczenie rozkładu. Jeśli kurtoza=3 to rozkład zmiennej jest taki jak normalny (Gaussa), jeśli K>3 to większe spłaszczenie rozkładu niż w rozkładzie normalnym, jeśli K<3 to mniejsze spłaszczenie.

• standaryzowany współczynnik skośności
  

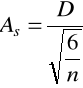
• standaryzowany współczynnik kurtozy
  

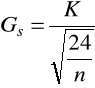
• współczynnik zmienności
  

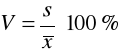
Funkcja gęstości

Funkcja gęstości jest krzywą powstałą na podstawie histogramu. Każda zmienna ma swoją własną krzywą gęstości. Najbardziej rozpowszechnioną w przyrodzie jest krzywa gęstości rozkładu Gaussa (rozkładu normalnego).

Ogólny wzór tej krzywej gęstości to: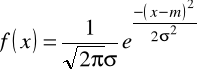

Gdzie: σ - odchylenie standardowe (dla całej populacji), m - wartość oczekiwana, e=2,7172.

W wypadku gdy mamy do czynienia z próbką w miejsce σ i m wstawiamy wartości ich estymatorów (czyli najczęściej średnią arytmetyczną oraz odchylenie standardowe s).

Standaryzacja zmiennej losowej do rozkładu normalnego:

W tablicach statystycznych mamy dostęp tylko do zestandaryzowanego rozkładu normalnego N(0,1) (tzn., że wartość oczekiwana wynosi 0 a odchylenie standardowe 1). W przypadkach empirycznych zazwyczaj wartości te różnią się od wzorcowych. Dlatego konieczne jest ich zestandaryzowanie.

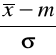
Wówczas dla otrzymanej wartości można odczytać wartość tablicową z tablicy dystrybuanty rozkładu normalnego.

Tablice statystyczne można np. znaleźć pod następującymi adresami stron www:

http://math.uc.edu/~brycw/classes/148/tables.htm

http://fsweb.berry.edu/academic/education/vbissonnette/tables/tables.html

---