Model Ekonometryczny
Model jednorównaniowy dla zmiennej endogenicznej - zużycia gazu z sieci w hektometrach sześciennych w gospodarstwach domowych w latach 1980-1996. Model oparty jest więc na 17 obserwacjach. Kształtowanie się zmienności zużycia gazu w gospodarstwach domowych początkowo starałam się wyjaśnić w oparciu o trzy zmienne egzogeniczne:
import gazu w hm3
długość sieci gazowej w km
ilość gospodarstw domowych w tys. szt.
Po oszacowaniu parametrów strukturalnych modelu okazało się jednak, że zmienna objaśniająca: ilość gospodarstw domowych nie wpływa istotnie na zmienną objaśnianą. Przyczyną złego dopasowania jest zapewne fakt, iż nie każde gospodarstwo ma dostęp do sieci gazociągowej, zatem użycie tej zmiennej jest nieco mylące. Po odrzuceniu jej, model oparty został na dwóch pozostałych zmiennych.
Założenia modelu: pomiędzy zmienną objaśnianą Yt, a zmiennymi objaśniającymi zachodzi związek liniowy, zakłócony przez addytywny składnik losowy ξt o rozkładzie normalnym o wartości oczekiwanej równej zero i stałej wariancji.
1. Postać równania liniowego modelu
Yt = β0 + β1X1t + β2X2t + ξ t
zmienna objaśniana (endogeniczna) : Yt - zużycie gazu w hm3 w gospodarstwach domowych
zmienne objaśniające (egzogeniczne) : X1t - import gazu w hm3, X2t - długość sieci gazowej w km
parametry strukturalne: β0 , β1, β2
składnik losowy : ξt
t = 1,2, ... ,17 - numer obserwacji
2. Oszacowanie parametrów strukturalnych
Ŷt = - 1109,2 + 0,95497 X1t + 0,05568 X2t + ξt
(941,2755) (0,15697) (0,0070133)
β0 = - 1109,2 nieznany parametr został oszacowany na podstawie 17 obserwacji na
poziomie - 1109,2 z dokładnością ± 941,2755
β1 = 0,95497 - jeśli import zwiększy się o jeden hektometr sześcienny, to zużycie gazu w gospodarstwach domowych wzrośnie o 0,95497 hektometra sześciennego, ze średnim błędem ± 0,15697
β2 = 0,05568 - jeśli długość sieci gazowej wzrośnie o jeden kilometr, to oczekuje się, że zużycie gazu w gospodarstwach domowych wzrośnie o 0,05568 hektometra sześciennego, ze średnim błędem ± 0,0070133
3. Syntetyczne miary dopasowania
Współczynnik determinacji R2
R2 = 0,94029 - model empiryczny wyjaśnia 94% rzeczywistej zmienności zużycia gazu
![]()
Skorygowany współczynnik determinacji
Obie wartości współczynników nie różnią się znacznie od siebie, co oznacza, że nie występuje „efekt pozornego wyjaśnienia”.
R = 0,96968 - występowało silne skorelowanie rzeczywistych i teoretycznych wartości zużycia gazu w latach 1980 - 1996.
Współczynnik zbieżności φ2
φ2 = 1 - 0,94029 = 0,05971 - ok. 6% zmienności rzeczywistego zużycia gazu nie zostało wyjaśnione przez model, co oznacza, że kształtuje się pod wpływem innych czynników, nieuwzględnionych bezpośrednio w modelu.
Standardowy błąd resztowy:
δξ = 486,2398 - przeciętnie, wartości rzeczywiste zużycia gazu odchylają się od jego wartości teoretycznych Yt (tj. wyznaczonych na podstawie modelu empirycznego)
o ± 486,2398 hm3
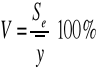
Współczynnik zmienności losowej V
![]()
Średni błąd resztowy stanowi 6,14% średniej wartości zużycia gazu w badanym okresie.
Weryfikacja ekonomiczna
Zarówno znaki jak i wartości ocen parametrów strukturalnych należy uznać za rozsądne.
4. Weryfikacja statystycznej istotności ocen parametrów strukturalnych
a) Indywidualne hipotezy istotności ocen parametrów strukturalnych
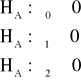
Hipotezy mają postać:
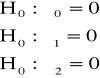
Liczba stopni swobody , w omawianym przypadku, jest równa (T - K - 1) = 17 - 2 - 1 = 14. Przy poziomie istotności α = 0,05, statystyka t-Studenta przyjmuje wartość krytyczną
t0,05 = 2,145.
Wartości odpowiednich statystyk wynoszą: t0 = -1,1784, t1 = 6,0839, t2 = 7,9391
Ponieważ zachodzi:
t0= 1,1784 < t0,05 = 2,145, to przyjmujemy H0, co oznacza, że parametr β0 nie różni się istotnie od zera, czyli nie wpływa na zmienna objaśnianą Yt. Ponadto wynika to również z faktu, że prawdopodobieństwo przyjęcia przez statystykę wartości nie mniejszej niż
-1,1784 jest równe Prob = 0,258. Prob = 0,258 > 0,05, więc H0 przyjmujemy.
t1= 6,0839 > t0,05 = 2,145, to odrzucamy H0 na rzecz HA, co oznacza, że parametr β1 różni
się istotnie od zera, czyli import gazu wpływa na zużycie gazu w gospodarstwach domowych. Prob = 0,000 < 0,05, więc H0 odrzucamy.
![]()
t2 = 7,9391 > t0,05 = 2,145, to odrzucamy H0 na rzecz HA, co oznacza, że parametr β1 jest statystycznie istotny, czyli długość sieci gazowej ma wpływ na zużycie gazu w gospodarstwach domowych. Prob = 0,000 < 0,05, więc H0 odrzucamy.
b) Łączna hipoteza istotności parametrów strukturalnych
Test istotności parametrów strukturalnych oparty jest na statystyce F-Snedecora.
Hipoteza istotności ma postać:
H0 : β1 = β2 = 0
HA : istnieje takie i, że βi ≠ 0
Wartość krytyczna statystyki F, dla poziomu istotności α = 0,05 oraz K = 2 i T - K - 1 = 14 stopni swobody wynosi F0,05 = 3,74
H0 należy odrzucić na rzecz HA, gdy F > Fα
Wartość statystyki F = 110,2255 > F0,05 = 3,74, czyli H0 odrzucamy na rzecz HA, co oznacza, że łącznie zmienne objaśniające istotnie wpływają na zużycie gazu w gospodarstwach domowych. Ponadto Prob = 0,000 < 0,05, co potwierdza powyższy wniosek.
5. Weryfikacja hipotez dotyczących braku autokorelacji składnika losowego
a) Test Durbina - Watsona
Statystyka DW wyznaczona na podstawie modelu wynosi DW = 1,9870. Hipoteza więc ma postać:
H0 : ρ = 0, reszty modelu nie są skorelowane
HA : ρ > 0, autokorelacja reszt występuje i jest dodatnia
ρ -współczynnik autokorelacji (rzędu pierwszego) składników losowych modelu.
Z tablic wartości krytycznych testu DW dla T = 17 obserwacji, K = 2 zmienne objaśniające i poziomu istotności α = 0,05, odczytuję dwie wartości krytyczne: górną du = 1,536 oraz dolną dl = 1,015.
H0 odrzucamy na rzecz HA wówczas, gdy DW < dl (autokorelacja dodatnia); oraz DW ∈
<dl; du> (nie można podjąć żadnej decyzji)
Ponieważ zachodzi: DW = 1,9870 > du = 1,536, H0 należy przyjąć, co oznacza, że autokorelacja reszt składnika losowego nie istnieje.
b) Test Godfreya - testowanie istotności autokorelacji dowolnego rzędu
Hipoteza ma postać:
H0 : σ1 = σ2 = ... = σp = 0 (brak autokorelacji rzędu p)
HA : istnieje takie i, że i σ ≠ 0, i = 1,2, ... , p
σ - określają zależność autokorelacyjną składników losowych modelu, którą można przedstawić jako: ξt = σ1 ξt-1 + σ2 ξt-2 + ... + σpξt-p + μt, gdzie μt to składnik czysto losowy z wartością oczekiwaną równą zero, stałą wariancją oraz zerowymi kowariancjami.
Statystyka ta ma rozkład χ2(p) oraz odpowiednik w postaci rozkładu F (p, T - p - (k + 1)), gdzie p oznacza maksymalny rząd autokorelacji podlegający badaniu.
χ2 obliczone na podstawie modelu wynosi χ2sc(1) = 2,2644. Przyjmując 5% poziom istotności H0 należy odrzucić dla Prob ≤ 0,05. Dla Prob > 0,05 nie ma podstaw do odrzucenia hipotezy zerowej.
Wartość próbkowa statystyki χ2sc(1) = 2,2644 z wartością Prob = 0,132, co oznacza, że H0 należy przyjąć.
Statystyka Fsc (1, 13) = 1,9977 z wartością Prob = 0,181. H0 należało by odrzucić dopiero na poziomie istotności α ≥ 0,181. Dla α = 0,05 nie ma podstaw do odrzucenia H0 o braku autokorelacji składników losowych, reszty modelu nie są względem siebie zależne.
6. Testowanie poprawności wyboru postaci analitycznej modelu
Test Ramseya
Hipoteza ma postać:
H0 : funkcja modelu jest liniowa p = 1
HA : funkcja modelu nie jest liniowa (jest p-tego rzędu, p > 1)
Statystyka ma rozkład χ2F (p) oraz odpowiednik w postaci rozkładu F (p, T - p -(K + 1))
Wartość próbkowa statystyki χ2F (1) = 3,045 z wartością Prob = 0,081, co oznacza, że H0 odrzucamy dopiero na poziomie istotności α ≥ 0,081. Dla α = 0,05 nie ma podstaw do
odrzucenia H0 zakładającej liniową postać modelu.
Statystyka Fsc (1, 13) = 2,8366 z wartością Prob = 0,116. H0 należało by odrzucić dopiero na poziomie istotności α ≥ 0,116. Dla α = 0,05 nie ma podstaw do odrzucenia H0.
Oba testy pozwalają na wnioskowanie, że model liniowy jest właściwą postacią opisu zależności zużycia gazu od importu gazu i długości sieci gazowej w latach 1980 - 1996.
7. Testowanie normalności rozkładu składników losowych
Test Jarque'a - Bera
Hipoteza ma postać:
H0 : ξt ma rozkład normalny
HA : ξt nie ma rozkładu normalnego
Statystyka J -B ma rozkład χ2 o dwóch stopniach swobody. Krytyczna wartość pochodząca z rozkładu χ2(2) i poziomu istotności α = 0,05 wynosi χ20,05 = 5,991. Ponieważ zachodzi:
J - B = 4,2738 < χ20,05 = 5,991, więc wnioskujemy, że nie ma podstaw do odrzucenia H0, czyli składniki losowe mają rozkłady normalne. Ponadto wartość Prob = 0,118 > 0,05, co potwierdza wyżej wysunięty wniosek.
8. Testowanie heteroskedastyczności rozkładu składników losowych
Hipoteza ma postać:
H0 : σ2ξt = σ2ξ , t = 1,2, ... , T
HA : wariancja nie jest stała
Statystyka testu ma dwa sprawdziany χ2(1) oraz F (1, T - 2)
χ2(1) = 3,1733 z wartością Prob = 0,075. H0 można odrzucić dopiero na poziomie α ≥ 0,075, więc dla α = 0,05 nie ma podstaw do odrzucenia H0.
F(1, 15) = 3,4426 z wartością Prob = 0,083 > 0,05, więc nie ma podstaw do odrzucenia H0.
Na podstawie testu χ2 i F można wnioskować, że rozkład składnika losowego nie jest heteroskedastyczny, czyli charakteryzuje się stałością wariancji.
9. Testowanie losowości reszt
Test serii
Hipoteza ma postać:
H0: reszty modelu mają charakter losowy
HA: reszty modelu nie mają charakteru losowego
a - reszty dodatnie a = 10
b - reszty ujemne b = 7
k - liczba serii
b, a, a, b, b, a, b, b, a, b, a, a, a, a, a, a, b
k = 9
Dla α = 0,05 , a = 10 oraz b = 7 wartość krytyczna wynosi kα = 5
k = 9 > kα = 5, nie ma więc podstaw do odrzucenia H0 , mówiącej o losowym charakterze reszt modelu.
Wniosek ogólny: model spełnia wszystkie kryteria weryfikacji i dane są dobrane tak, aby zmienne objaśniające: import gazu oraz długość sieci gazowej istotnie wyjaśniały zużycie gazu.
Załączniki :
Wykaz danych modelu (Rocznik statystyczny: 1980 -1997)
Wydruk estymacji przeprowadzonej metodą najmniejszych kwadratów ( źródło - MICROFIT )
Wydruk testów diagnostycznych ( źródło - MICROFIT )
Wykres dopasowania danych empirycznych do rzeczywistych ( źródło - MICROFIT )
WYKAZ DANYCH MODELU
Obserwacje |
Zużycie gazu w hm3 |
Import gazu w hm3 |
Długość sieci gazowej w km |
Ilość gospodarstw w tys. szt. |
C |
1980 |
5054 |
5312 |
22402 |
10052 |
1,0000 |
1981 |
5382 |
5261 |
23647 |
10165 |
1,0000 |
1982 |
5926 |
5621 |
25204 |
10334 |
1,0000 |
1983 |
5487 |
6007 |
26745 |
10474 |
1,0000 |
1984 |
5993 |
6015 |
28356 |
10692 |
1,0000 |
1985 |
6602 |
5898 |
30046 |
10867 |
1,0000 |
1986 |
7222 |
7135 |
32165 |
11055 |
1,0000 |
1987 |
7823 |
7531 |
34640 |
11206 |
1,0000 |
1988 |
8188 |
7487 |
37825 |
11101 |
1,0000 |
1989 |
8556 |
7905 |
41175 |
11057 |
1,0000 |
1990 |
9406 |
7836 |
45827 |
11967 |
1,0000 |
1991 |
9542 |
7752 |
52033 |
11953 |
1,0000 |
1992 |
9785 |
7628 |
60752 |
11967 |
1,0000 |
1993 |
9891 |
7458 |
67981 |
11744 |
1,0000 |
1994 |
9822 |
6942 |
74595 |
11592 |
1,0000 |
1995 |
10486 |
6772 |
79352 |
12053 |
1,0000 |
1996 |
9353 |
7358 |
83699 |
12498 |
1,0000 |
źródło: Rocznik Statystyczny, lata 1980 - 1996
1
1
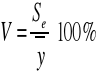
![]()
![]()
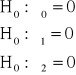

![]()
Wyszukiwarka
Podobne podstrony:
Model Ekonometryczny2, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Model ekonometryczny, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Teoria konsumenta, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
17, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
pomoc publiczna, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
konsorcjum gospodarcze, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Ś z integracji europejskiej, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Logistyka, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Egzaminu przedmiotu Normalizacja, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
Folie do tematow 1-2, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
44, Studia, STUDIA PRACE ŚCIĄGI SKRYPTY
więcej podobnych podstron