Zadanie 5.

Punkty przegięcia są to takie punkty, w których styczna do funkcji przechodzi z jednej strony na drugą. W związku z tym punkty przegięcia to punkty dla których pochodna drugiego rzędu zmierzająca od strony prawej przyjmuje wartości dodatnie, a z lewej ujemne i vice versa.

Rozwiązanie:

Najpierw liczę pochodną pierwszego rzędu, a później wyliczę pochodną drugiego rzędu.

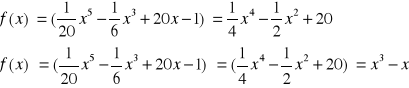
Następnie przyrównuję pochodną drugiego rzędu do 0.

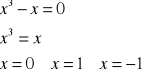
Dla tych trzech punktów obliczam granice prawo i lewostronne.

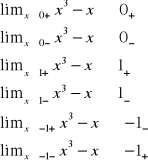
Granice te policzyłam analogicznie do twierdzenia 5.4.16 na str.84(Krysicki,Włodarski)

Zostaje nam do skonstruowania tabelka:

-∞	(-∞;-1)	-1	(-1;0)	0	(0,1)	1	(1,+∞)	-∞	Argumenty
-	-	0	+	0	-	0	+	+	2ga Pochodna

Odpowiedź: Punkty przegięcia to x=-1, x=0 i x=1.

---