LISTA 1

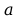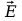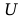1. W trzech rogach kwadratu o boku znajdują się ładunki: q, 2q i 3q. Znaleźć natężenie i potencjał pola elektrycznego w czwartym rogu tego kwadratu.

2. Które z podanych pól wektorowych może być polem magnetycznym (b – stała):

a) ,

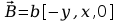b) ,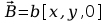

c) ,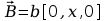

d) .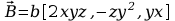

3. Pierścień o promieniu a jest jednorodnie naładowany ładunkiem q. Policzyć natężenie pola elektrycznego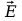 w punkcie leżącym na osi symetrii obrotowej pierścienia w odleg lości x od jego środka.

4. Określić natężenie pola elektrycznego 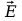w odległości 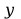od nieskończenie długiego jednorodnie naładowanego pręta. Na jednostkę długości pręta przypada ładunek λ.

LISTA 2

1. Wychodząc z równań Maxwella wyznaczyć natężenie pola elektrycznego w całej przestrzeni dla:
a) jednorodnie naładowanej kuli izolatorowej o promieniu R i ładunku Q,

b) kuli metalowej o promieniu R i ładunku Q,

c) jednorodnie naładowanego nieskończonego prostoliniowego pręta o gęstości liniowej ładunku λ,

d) nieskończonej jednorodnie naładowanej płaszczyzny o gęstości powierzchniowej ładunku σ.

2. Wychodząc z równań Maxwella wyznaczyć indukcję pola magnetycznego w całej przestrzeni dla:

a) nieskończonego prostoliniowego pręta, przez który płynie stały w czasie prąd o natężeniu I,

b) nieskończonego solenoidu, przez który płynie stały w czasie prąd o natężeniu I (liczba zwojów na jednostkę długości solenoidu wynosi n).

LISTA 3

1. W jednym z naroży (A) sześcianu ABCDEFGH znajduje się punktowy ładunek Q. Policz strumienie pola elektrycznego przez boki ABCD i EFGH tego sześcianu ?

2. W pewnym obszarze wektor natężenia pola elektrycznego jest równy (we współrzędnych

sferycznych) 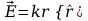, gdzie k jest stałą. Znaleźć gęstość ładunku objętościowego q_v. Wyznaczyć

całkowity ładunek zawarty w kuli o promieniu R i środku w początku układu współrzędnych.

3. Pierścień o promieniu a jest jednorodnie naładowany ładunkiem Q. Policzyć potencjał pola elektrycznego w punkcie leżącym na osi symetrii obrotowej pierścienia w odległości r od jego środka.

4. Wyznacz potencjał pola elektrycznego dla pól z zadania 1, a) i b) na poprzedniej liście zadań.

5. Natężenie pola elektrycznego w pewnym obszarze wynosi 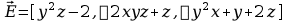. Znajdź potencjał tego pola w tym obszarze.

LISTA 4

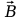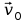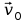1. Cząstka o ładunku q wpada w jednorodne pole magnetyczne z prędkością początkową , tak, że kąt między i 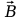wynosi α. Znaleźć tor ruchu ładunku. Znaleźć promień orbity po której porusza się ładunek jeśli kąt α jest równy π/2.

2. Przewodnik (prosty drut) o długości l, w którym płynie prąd o natężeniu i znajduje się w prostopadłym do niego jednorodnym polu magnetycznym B. Korzystając z wzoru na siłę Lorentza oraz zależności określającej gęstość powierzchniową prądu j = nev, gdzie e jest ładunkiem elektronu, n jest koncentracją elektronów (liczbą elektronów na jednostkę objętości), a v prędkością unoszenia elektronów, pokazać, że pole magnetyczne działa na przewodnik siłą o wartości F = ilB.

3. Obliczyć siłę działającą na umieszczony w polu magnetycznym B przewodnik w kształcie półokręgu o promieniu R, w którym płynie prąd o natężeniu I. Linie indukcji pola magnetycznego są prostopadłe do płaszczyzny w której leży przewodnik.

4. Dwa równoległe długie przewodniki prostoliniowe znajdują się w odległości d od siebie. Przez przewodniki płyną w tym samym kierunku prądy o natężeniach I₁ i I₂. Jaką pracę należy wykonać (na jednostkę długości przewodników), aby rozsunąć te przewodniki do odległości 2d?

5. Dwie długie, wzajemnie równoległe, szyny miedziane ustawione pionowo w odległości l, są zwarte w górnym końcu oporem R. Znajdują się one w jednorodnym polu magnetycznym o indukcji B, prostopadłym do płaszczyzny szyn. Wzdłuż szyn spada bez tarcia przewodnik o masie m. Znaleźć wartość prędkości spadania, jaka się ostatecznie ustali. 9