Wstęp teoretyczny

Dualizm korpuskularno-falowy to teoria według której w zależności od sytuacji światło może być rozpatrywane jako cząsteczka, gdyż posiada masę, energię, ulega efektowi Comptona (w którym w podczas zderzenia fotonu z elektronem, przekazuje temu drugiemu część energii i odchyla się od początkowego toru ruchu), czy efektowi fotoelektrycznemu (w którym foton padający na powierzchnię metalu o energii wyższej od pracy wyjścia wybija z niej elektron) lub jako fala gdyż posiada długość, częstotliwość, ulega zjawisku dyfrakcji (zmiany kierunku rozchodzenia się fali w po napotkaniu na przeszkodę) czy interferencji (wzmacniania lub wygaszania fal w wyniku ich nakładania się). W świecie optyki obowiązuje wiele praw, najważniejsze z nich to prawo odbicia i załamania. Pierwsze z nich mówi, że kąt padania równy jest kątowi odbicia, a drugie, że stosunek sinusa kąta padania do sinusa kąta załamania jest stały dla danych dwóch ośrodków. W obu przypadkach promień padający, załamany i prosta prostopadła do po powierzchni w punkcie załamania leżą w jednej płaszczyźnie. Przytoczony wyżej stosunek sinusów kątów jest wielkością opisującą parę ośrodków przez które przechodzi światło i nazywany jest względnym współczynnikiem załamania światła - ośrodka drugiego względem pierwszego. Gdy jednym z ośrodków jest próżnia, wyznaczyć można bezwzględny współczynnik załamania światła będący stosunkiem prędkości światła do prędkości światła rozchodzącego się w danym ośrodku. Porównując współczynniki bezwzględne dwóch ośrodków dochodzimy do wzoru na względny współczynnik załamania światła:

Celem tego ćwiczenia było poznanie budowy i zasady działania mikroskopu optycznego oraz metody pomiaru współczynnika załamania światła przy jego użyciu. Mikroskop to urządzenie optyczne służące do obserwacji małych, zwykle niewidocznych gołym okiem obiektów. Składa się on z obiektywu, okularu, tubusa w którym następuje formowanie powiększonego obrazu pośredniego, śruby mikrometrycznej do wstępnej regulacji odległości oraz mikrometrycznej do ustalenia ostrości i źródła światła (np. lusterka). Obraz obiektu najpierw ulega wstępnemu powiększeniu i odwróceniu, gdy promienie światłą przechodzą przez obiektyw - w ten sposób powstaje obraz rzeczywisty wewnątrz tubusa, który następnie poprzez okular ulega powiększeniu. Ostatecznie obraz jest odwrócony, powiększony i pozorny. Rozważając bieg promieni świetlnych przechodzących od spodu próbki i ulegających załamaniu na granicy powietrze/badany materiał można stwierdzić, że stosunek sinusa kąta załamania do sinusa kąta odbicia (dla małych kątów równych stosunkowi tangensów tych kątów) jest równy stosunkowi rzeczywistej grubości płytki do odległości obrazu pozornego powierzchni dolnej, od górnej powierzchni badanej próbki. Stosunek ten równy jest współczynnikowi załamania światła próbki względem powietrza, który należało wyznaczyć w celu identyfikacji próbek. W ramach ćwiczenia dokonywano pomiarów grubości d, trzech nieznanych płytek spośród: szkła, pleksi oraz kwarcu. Na początku grubość każdej z nich zmierzono za pomocą śruby mikrometrycznej. Następnie po zamocowaniu jej w mikroskopie ustawiono ostrość na plamę kreskę namalowaną flamastrem (różnych kolorów) znajdującą się na dolnej powierzchni płytki i odczytano wskazanie grubościomierza a₁. Po czym podniesiono tubus na wysokość a₂ przy której ostry był obraz namalowanej flamastrem kreski znajdującej się na górnej powierzchni płytki. Każdy pomiar wykonywano po sześć razy w różnych miejscach, dla każdej z próbek. Różnica odległości wysokości

a₂-a₁ wyznaczała odległość obrazu pozornego od górnej powierzchni płytki a.


Otrzymane wyniki zestawiono w tabeli:

Pomiar „a”	Próbka 1. [mm]	Próbka 2. [mm]	Próbka 3. [mm]
1.	2,37	1,25	0,76
2.	2,35	1,21	0,72
3.	2,4	1,2	0,72
4.	2,3	1,14	0,70
5.	2,37	1,19	0,63
6.	2,37	1,05	0,71
Średnia „a”	2,36	1,17	0,71
Pomiar „d”
1.	3,65	1,97	0,96
2.	3,64	1,98	0,95
Średni „d”	3,645	1,975	0,955

Następnie obliczono współczynnik załamania ze wzoru

n₁=1,544
n₂=1,68
n₃=1,35

Następnie obliczono średni błąd kwadratowy ze wzoru: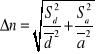

, gdzie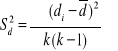
;

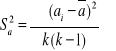
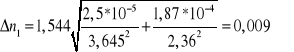
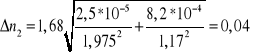
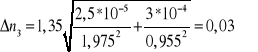
Co daje następujące wyniki końcowe:

n₁=1,544
0,009
n₂=1,68
0,04
n₃=1,35
0,03

Dla danych tablicowych:
n_kwarc/pow.=1,46
n_pleksi/pow.=1,489
n_{szkło.crown/pow.}=1,54
n_{kszkło.flint/pow.}=1,66

Wnioski:
Powyższe badanie umożliwiło mi zapoznanie się z zasadą działania mikroskopu oraz przypomnienie zasad optyki. Jak również zaznajomienie się z metodami identyfikacji materiałów próbek przezroczystych.

Na niepewności pomiaru miały wpływ takie czynniki jak:
- niedokładność urządzeń pomiarowych - niepewność związana z ustaleniem odległości tubusa od stolika przy użyciu śruby mikrometrycznej
- klasa urządzeń pomiarowych - mikroskop optyczny, śruba mikrometryczna
- jakości oraz grubości materiałów użytych w doświadczeniu
- błędy wynikające z przyjętej dokładności prowadzenia obliczeń
- wpływ czynnika ludzkiego - ostrość jest pojęciem względnym, każda osoba mierząca tę odległość ustawi inną ostrość, w przypadku mikroskopu odczucia te będą dość zbliżone, ale jednak mogą się nieznacznie różnić

Dodatkowo na niepewności pomiaru wpływ mogła mieć aberracja chromatyczna - światło pochodzące z kresek namalowanych różnymi kolorami rozchodziło się szybciej (dla czerwonego) czy wolniej (dla niebieskiego) i w związku z tym na różnej odległości ustalała się ostrość obrazu. Ujawnia się to poprzez różnice w pomiarach „a” dla danej płytki dla pomiarów 2. I 3. gdzie kreski były namalowane flamastrami różnych kolorów w odróżnieniu od 1. na której wyrysowane były wyłącznie

czerwone kreski.

Na podstawie porównania wyników obliczonych wielkości fizycznych z wartościami tablicowymi, można zidentyfikować dwie spośród trzech próbek. Pierwszą z nich, było prawdopodobnie szkło typu crown o dużej zawartości tlenku potasu, charakteryzujące się dużą przejrzystością. Drugą z nich mogło być ciężkie szkło typu flint. Określenie z czego była wykonana najcieńsza próbka jest prawie niemożliwe, gdyż wartości tabelaryczne dla tej wartości przedstawiają głównie ciecze, które nie były przedmiotem badań. Jednakże już niewielkie odchylenie od pomiaru zmienia diametralnie wynik w przypadku tak małych liczb. Na przykład gdyby przyjąć wartość 4. pomiaru „a” zamiast średniej dla próbki 3., (a=0,654 mm), współczynnik załamania światła wynosiłby 1,46 co stanowiłoby, że badana

próbka była wykonana z kwarcu.

Powyższe rozważania pozwalają skonstatować, że im cieńsze są próbki tym mniej dokładny jest pomiar, a co za tym idzie mniej wiarygodny jest wynik próby identyfikacji materiału.
Co prowadzi do wniosku, że badanie to jest dość dobrą metodą weryfikacyjną dla próbek o grubości powyżej dwóch milimetrów.

Wiktor Adamski, Nanotechnologia, semestr II, grupa 1., gr. laboratoryjna 14.

---