Uczelnia Zawodowa Zagłębia Miedziowego

LUBIN

FIZYKA

LABOLATORIUM

ĆWICZENIA

TEMAT: BADANIE EFEKTU HALLA

Prowadzący: Wykonał:

Mgr Stanisław Lis Biskup Bernard

ZPP II grupa A

Uczelnia Zawodowa Zagłębia Miedziowego LUBIN	FIZYKA LABORATORIUM	Ćwiczenie nr 3
Prowadzący ćwiczenie Podpis………………….	Tytuł ćwiczenia: Badanie efektu Halla	Data wykonania ćwiczenia
autor: ZPP II rok, gr. A	Przyjęcie wykonania ćwiczenia przez prowadzącego	Końcowa ocena ćwiczenia/sprawozdanie/

WSTĘP

EFEKT HALLA.

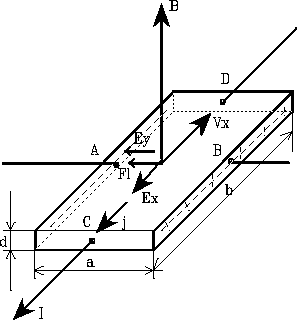
Jeżeli płytkę z metalu lub półprzewodnika włączymy w obwód [prądu stałego i umieścimy w polu magnetycznym, którego wektor indukcji B jest prostopadły do powierzchni płytki i do kierunku płynącego prądu elektrycznego, to między punktami na bocznych powierzchniach płytki wytworzy się różnica potencjałów UH, zwana napięciem Halla.

Załóżmy, że nośnikami prądu są elektrony. Jeżeli do płytki przyłożymy napięcie, to w razie braku pola magnetycznego przez próbkę będzie płynął prąd o natężeniu I. Wytworzone w próbce pole elektryczne o natężeniu Ex będzie skierowane zgodnie z kierunkiem płynącego prądu, natomiast elektrony poruszać się będą w kierunku przeciwnym polu z prędkością vx. Gęstość prądu płynącego przez płytkę określona jest wzorem:

j = e n vx

Natężenie prądu I można określić jako iloczyn gęstości prądu i powierzchni S prostopadłej do kierunku wektora gęstości prądu , zatem

I = e n vx S.

W obecności pola magnetycznego o indukcji B, na elektrony poruszające się w tym polu z prędkością vx, działa siła Lorentza

FL = -e (vx B).

Tak więc każdy elektron w płytce poruszający się z prędkością vx, zostaje odchylony od swego początkowego kierunku ruchu. Wskutek zmiany torów elektrony gromadzą się na jednej z krawędzi płytki, natomiast na drugiej wytwarza się niedobór elektronów. Dzięki temu powstaje dodatkowe pole elektryczne o natężeniu Ey. Proces gromadzenia się ładunków trwa tak długo, aż powstałe pole poprzeczne Ey, działające na elektrony z siłą

Fy = -eEy

zrównoważy siłę Lorentza.

Dla warunków równowagi możemy zapisać

Fy = FL

skąd możemy otrzymać wyrażenie określające napięcie Halla

UH = I B,

w którym

gdzie d - wysokość płytki.

Mierząc natężenie prądu I płynącego przez płytkę, napięcie Halla UH oraz znając współczynnik , można wyznaczyć indukcję magnetyczną B. Urządzenie służące do wyznaczania indukcji magnetycznej nazywa się hallotronem, współczynnik zaś czułością hallotronu.

ĆWICZENIE NR 3

1. Spis przyrządów

1. - hallotron umieszczony w polu magnetycznym wytworzonym przez magnesy trwałe. Magnesy zamocowane są tak aby możliwy był pomiar zmian orientacji pola magnetycznego względem płaszczyzn hallotronu,

2. - zasilacz hallotronu,

3. - miliamperomierz do pomiaru natężenia prądu sterującego,

4. - woltomierz do pomiaru napięcia Halla.

2. Cel ćwiczenia

5. Wyznaczenie charakterystyk hallotronu.

6. Wyznaczenie czułości hallotronu.

7. Wyznaczenie koncentracji elektronów swobodnych.

8. Wyznaczenie czułości kątowej układu.

3. Przebieg pomiarów

1. połączyć układ zasilający hallotron.

2. wyznaczyć zależność napięcia Halla U_H od indukcji magnetycznej przy ustalonym natężeniu prądu płynącego przez hallotron I_S = const = 10 mA. Włączyć woltomierz oraz zasilacz hallotronu. Obrócić magnesy w położenie przy którym napięcie Halla U_H = 0 - kierunek pola magnetycznego jest wtedy równoległy do powierzchni hallotronu - zanotować to położenie jako α0 . Wykonać pomiary zależności napięcia Halla od kąta pomiędzy kierunkiem indukcji magnetycznej B i powierzchnią hallotronu. Pomiary wykonać w przedziale od 0˚do 360˚ co 10˚.

3. wyznaczyć zależność napięcia Halla U_H od natężenia prądu płynącego przez hallotron I_S, przy ustalonej wartości indukcji magnetycznej B. Ustawić magnesy pod kątem wskazanym przez prowadzącego (160˚). Przeprowadzić pomiary zależności napięcia Halla U_H od natężenia prądu sterującego I_S w zakresie od 1mA do 15mA co 1mA.

4. Opracowanie wyników

1. Narysować wykres zależności napięcia Halla od kąta odczytanego z podziałki hallotronu.

2. Korzystając z tego wykresu odczytać wartości α0 przy której U_H = 0.

3. Obliczyć maksymalną wartość czułości kątowej hallotronu Δ U_H /Δα.

4. Narysować wykres zależności napięcia Halla od wartości składowej normalnej indukcji Bn = B0 sin(α-α0).

5. Narysować wykres zależności napięcia Halla U_H od natężenia prądu I_S płynącego przez hallotron.

6. Korzystając z regresji liniowej obliczyć współczynniki kierunkowe prostych opisujących zależności U_H (B) przy I_S = const oraz U_H (I_S ) przy Bn=const.

7. Korzystając z wartości współczynników kierunkowych obliczuć czułość hallotronu γ.

8. Oszacować niepewność wyznaczenia czułości hallotronu Δγ oraz Δγ/γ [%].

9. Obliczyć koncentrację elektronów swobodnych n korzystając z wyrażenia:

Gdzie:

d - grubość płytki hallotronu (d=2μm)

e - ładunek elementarny (e=1,6·10‾¹9 C)

przyjąć: B0=(0,500±0,05)T

Δd/d=5%

9. Niepewności pomiarowe Δ U_H oraz Δ I_S należy obliczyć zgodnie z wskazówkami , które znajdują się w instrukcji do mierników.

10. Obliczyć względną niepewność koncentracji Δn/n[%]=Δd/d[%]+Δγ/γ[%]

4. Tabele z wynikami pomiarów

1. Wyznaczenie zależności napięcia U_H od indukcji magnetycznej przy ustalonym natężeniu prądu I_S = const = 10 mA

α0 = 85⁰

2. Wykres zależności napięcia Halla U_H od natężenia prądu I_S płynącego przez hallotron

B = const (160⁰)

3. Wykres zależności napięcia Halla U_H od wartości składowej normalnej indukcji B_n.

OBLICZENIA

Obliczenie czułości hallotronu

Pomiar 2

Średnia czułość hallotronu wyznaczona dla pomiarów 2 γ  = 47,13

przy:

- B_M = const

- T = 0,5

Pomiar 3

Średnia czułość hallotronu wyznaczona dla pomiaru 3 γ  = 48,79

przy:

- I_S = const

- I = 10 [mA]

Z pomiarów 2 i 3 wynika, że czułość hallotronu wynosi:

γ  (γ  γ  

γ  (,  ,  

γ  ,

Oszacowanie niepewności czułości hallotronu γ oraz γ/γ [%]

Do obliczeń wziąłem tabelę z pomiarami 2. Pomiar wykazuje zależność napięcia od natężenia przy stałej indukcji

B= const.

Niepewność względna ε

Obliczenie koncentracji elektronów swobodnych n

gdzie

e = 1,6 ^. 10 ^-19 C

d = 2 m = 2 ^. 10 ^-6 m

γ = 47,96

   mA

  , 

[n] =

Δd / d = 5%

Względna niepewność koncentracji

Δn / n [%] = Δd / d + Δλ / λ

Δn / n [%] = 8,01%

Błąd bezwzględny I_s = 10 mA

Błąd względny I_s

Błąd bezwzględny U_H = 26 mV

Błąd względny U_H

Współczynniki kierunkowe prostych

WNIOSKI

1. Charakterystyka Uh(B) przy stałym prądzie sterującym Is . Charakterystyka ta jest w przybliżeniu liniowa, jest to zjawisko bardzo korzystne ponieważ zapewnia bardzo szeroki zakres przetwarzania hallotronu. Taki układ pracy można stosować min. do pomiarów indukcji magnetycznej.

2. Charakterystyka Uh(Is) przy stałej indukcji. Na podstawie charakterystyki widzimy, że czułość hallotrony rośnie wraz ze wzrostem prądu sterującego hallotron. Przez wzrost czułości rozumiemy wzrost napięcia na zaciskach hallotronu przy stałej indukcji.

3. Liniowość powyższych zależności wykorzystywana jest szeroko w przemyśle. Produkowane jest wiele typów hallotronów (elementów, w których powstaje zjawisko Halla polegające na powstaniu różnicy potencjału w przekroju poprzecznym przewodnika, w którym płynie prąd), oraz podzespołów hallotronowych. Przykładami takim elementów są specjalne sądy hallotronowe, bezstykowe przełączniki sygnałów elektrycznych, szerokopasmowe głowice odczytujące zapis magnetyczny. Wśród urządzeń należy wymienić min.: mierniki indukcji pola magnetycznego, specjalne silniki z komutatorami hallotronowymi, przeznaczone do urządzeń informatyki oraz przetworniki przesunięć liniowych i kątowych i wiele innych.

- 1 -

0,005 ^. 0,1

=

U_H [V]

I_S [A] ^. B [T]

gdzie :

U_H - napięcie Halla

Is - natężenie prądu sterującego

B - wartość indukcji pola magnetycznego przy danej wartości natężenia prądu magnesującego.

0,02

=

= 57,59

0,010 ^. 0,09

= 48

0,05

=

Pierwszy pomiar z tabeli

Pierwszy pomiar z tabeli

1

m³

47,96 ·1,6 ^. 10 ^{-19 .} 2^. 10 ^-6

1

n =

0,65 ^. 10 ²³

=

m³

1

ε =

Sx (odch. Stan. Poj. Pomiaru)

x (średnia arytmetyczna )

ε = 0,00682

Zaokrąglenie wyników pomiarów

γ  (,  ,

Δ Is =

0,5 ^. 10 mA

100 %

= 0,05 mA

= 0,5 %

Is

Δ Is

δ _Is =

^. 100 %

Δ U_H =

0,5 ^. 26 mV

100 %

= 0,13 mV

^. 100 %

= 0,5 %

U_H

Δ U_H

δ _UH =

Δγ

δ _UH = 0,5%

δ _Is = 0,5%

δ _B = 2%

δ _D = 5%

δγ  δ _UH + δ _Is + δ _B = 2,5%

Δγ  γ ( δ _UH + δ _Is + δ _B ) = 1,42

δn  δγ  δ _D = 3,55%

n= 0,65 _˙ 10 ²³

γ

Dla U_H (I_S) przy B = const

Współczynnik A = 2,198 _˙ 10 ^-2

Współczynnik B = 8,023 _˙ 10 ^{- 4}

Dla U_H (B) przy I_S = const = 10 mA

 ∈ ( 

Współczynnik A = 3,074 _˙ 10 ^{- 5}

Współczynnik B = 1,226 _˙ 10 ^{- 1}

Dla U_H (B) przy I_S = const = 10 mA

 ∈ (  

Współczynnik A = 1,152 _˙ 10 ^{- 3}

Współczynnik B = - 6,173 _˙ 10 ^{- 1}

---