TRANSFORMACJA RÓWNOKĄTNA WSPÓŁRZĘDNYCH PROSTOKĄTNYCH PŁASKICH

Przyjmując, że współrzędne punktów w układzie pierwotnym oznaczone są literami U i W, natomiast współrzędne punktów w układzie wtórnym literami X, Y oraz obie pary współrzędnych płaskich są parami współrzędnych izometrycznych, to funkcję odwzorowawczą, która zapewni równokątność odwzorowania, możemy napisać w postaci następującego szeregu odwzorowawczego:

gdzie:

a₀, b₀, a₁, b₁, a₂, b₂, ... - współczynniki liczbowe,

n - najnowszy wykładnik potęgi, czyli stopień transformacji.

Po wykonaniu działań matematycznych wynikających z powyższego wzoru można oddzielić część rzeczywistą od części urojonej.

Po uporządkowaniu wyrażeń otrzymamy:

Obliczenia za pomocą powyższych wzorów mogą sprawić pewne kłopoty, ponieważ kolejne iloczyny współczynników a_i lub b_i wyrażeń znajdujących się w nawiasach będą iloczynami liczb bardzo małych i liczb bardzo dużych.

W celu uniknięcia tych trudności można wprowadzić dwa nowe układy współrzędnych: u, w i x, y. Współrzędne u, w są zdefiniowane następującymi wzorami:

gdzie:

U₀, W₀ - są współrzędnymi wybranego punktu w układzie pierwotnym, leżącego w pobliżu środka ciężkości transformowanego zbioru punktów, natomiast k jest współczynnikiem liczbowym dobranym tak, aby średnia wartość |u| i |w| była zbliżona do jedności.

Współrzędne x, y są zdefiniowane wzorami:

Związek współrzędnych x, y i u, w ma następującą postać macierzową:

(*)

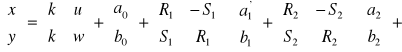
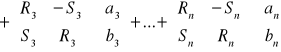
gdzie :

Do obliczania współczynników liczbowych a₀, b₀, a'₁, b₁, ... są wykorzystywane punkty łączne, czyli takie punkty, które mają znane współrzędne w układzie pierwotnym (U, W), jak i w układzie wtórnym (X, Y).

Dla każdego punktu łącznego można ułożyć dwa równania mające postać wzorów (*), w których niewiadomymi będą poszukiwane współczynniki. Jeżeli liczba punktów łącznych jest większa niż (n + 1) · 2 , gdzie n jest stopniem transformacji, to obliczanie współczynników przeprowadza się metodą najmniejszych kwadratów.

Równania poprawek dla każdego punktu łącznego mają następującą postać wynikającą z poniższego wzoru:

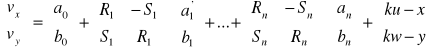
gdzie:

ku - x oraz kw - y są wyrazami wolnymi.

Stopień transformacji zwykle jest dobierany doświadczalnie na podstawie wielkości błędu średniego pojedynczej „obserwacji” m_o. Stopień transformacji jest z reguły tym większy, im większy jest obszar, na którym są rozrzucone transformowane punkty.

1

---