Sieci płaskie nazywamy zespół punktów geodezyjnych, zawierający przynajmniej dwa punkty znane, tj. punkty o ustalonych współrzędnych, i w którym dla wyznaczenia położenia n punktów zmierzono więcej niż 2n elementów geometrycznych. Podstawowym parametrem oceny dokładności przy wyrównaniu sieci płaskich jest błąd m₀. Wyraża się on wzorem:

gdzie v to błąd pozorny - różnica wartości średniej do wartości jednorazowej. Jeżeli błąd m₀ po wyrównaniu sieci jest większy niż przed wyrównaniem, to znaczy że sieć posiada błędy grube i wyrównanie trzeba powtórzyć.

Drugim ważnym elementem są wagi. Wagi obserwacji o błędach średnich

m₁, m₂, ..., m_n

nazywamy liczby

p₁, p₂, ..., p_n

odwrotnie proporcjonalne do kwadratów średnich błędów. Przy oznaczeniu czynnika stałego przez m₀ będzie:

,
, ....,
.

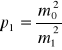
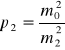
Czynnik m₀ w tych wzorach nosi nazwę średniego błędu spostrzeżenia o wadze jednostkowej, dla m_i = m₀ będzie bowiem p_i = 1. Niekiedy za błąd spostrzeżenia o wadze jednostkowej przyjmuje się jedność. Wówczas wagi staną się po prostu odwrotnościami kwadratów średnich błędów. Odwrotność wagi funkcji daje nam wartość q, która jest brana pod uwagę podczas wyrównania

Zasada Legendre'a mówi, że: układ obserwacji należy wyrównywać tak, aby suma kwadratów poprawek mnożona przez odpowiadające wagi była najmniejszością:

Kolejnym czynnikiem charakteryzującym dokładność przy wyrównaniu jest błąd położenia punktu m_p. Błąd ten określany jest jako przeciwprostokątna trójkąta o przyprostokątnych m_x i m_y, to znaczy

Przy analizach dokładnościowych odnoszących się do układów wyznaczających większą liczbę punktów można oczywiście posługiwać się wzorami wyznacznikowymi, staje się to jednak uciążliwe. Bardziej celowe jest wtedy stosowanie wzorów krakowianowych operujących pojęciem pierwiastka, który jest niezastąpiony przy rozwiązaniu bardziej skomplikowanych zagadnień rachunkowych. I tak na przykład dla jakiejś funkcji błąd wynosi:

gdzie

Elementy krakowianu kolumnowego ϕ łatwo jest obliczyć mnożąc go przez kolejne kolumny R (pierwiastek krakowianowy z wyrównania), co ma dawać znane elementy kolumny współczynnikowej f:

Następnym elementem jest elipsa błędu położenia punktów, którą można przedstawić za pomocą wykresu, gdzie a i b to półosie, a α - azymut półosi:

Wyrażają się one wzorami:

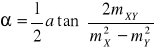
Najprostszym programem do wyrównania sieci jest program WinKalk, w którym podczas obliczania współrzędnych punktów sieci poziomej można otrzymać zarówno błąd m₀, jak i błędy m_x i m_y, z których powstaje błąd położenia punktu. Podobnymi programami są C-Geo oraz GeoNet, które mają większe możliwości pod względem wyrównania.

Następnie programy Mathcad i Excel to programy, w których można obliczyć wszystkie powyższe parametry. W programie Mathcad można je zapisać tak jak wyglądają w rzeczywistości. Natomiast w Excelu, tak jak w każdym arkuszu kalkulacyjnym, kolejne wzory należy przypisywać do danych cel (komórek). Także obliczenie błędu położenia punktu, bądź innej funkcji wykorzystując wzory krakowianowe nie stwarzają większych problemów.

Kolejnym programem jest program DOS-owski Poz86, w którym da się obliczyć błędy m₀ i m_p, ale także od razu elipsy błędu położenia punktów. Jest to program, który pozwala wyrównać daną sieć, a później przeanalizować i ocenić dokładności po wyrównaniu.

Literatura:

1. Rachunek wyrównawczy i obliczenia geodezyjne Stefan Hausbrandt

2. Teoretyczne podstawy opracowania wyników pomiarów geodezyjnych Włodzimierz Baran

3. www.softline.geo.pl

4. www.geonet.net.pl

5. Notatki z poprzednich semestrów

---