1.2. OBLICZENIA NA LICZBACH PRZYBLIŻONYCH

Liczbą przybliżoną, o znanym przybliżeniu, nazywa się taką liczbę x , dla której będzie spełniona nierówność

(1.1)

gdzie: x - nieznana dokładna (prawdziwa) wartość liczby,

x0 - znana wartość przybliżona danej liczby,

x - znany błąd wartości przybliżonej xo, zwany „błędem

krańcowym”, „granicą błędu” lub „błędem bezwzględnym”.

Liczba przybliżona jest znana, gdy znany jest przedział, w którym się ona znajduje.

1.2.1. Zapis liczb przybliżonych

Liczby przybliżone zapisuje się ten sposób, by błąd krańcowy nie przekraczał połowy jednostki ostatniej, zapisanej cyfry.

W ten sposób zapis x = 165,86 oznacza, że

a więc x mieści się w przedziale

165,855
x
165,865

Wartość błędu krańcowego wynosi tu

Pisząc = 3,14, widzimy od razu, że

3,14 - 0,510-2

3,14 + 0,510-2

błąd krańcowy zaś wynosi tu
= 0,510-2.

Wartość błędu krańcowego na ogół zapisuje się pod postacią

(1.2)

gdzie k jest ujemną lub dodatnią liczbą całkowitą.

Jeżeli liczbę przybliżoną zapisze się zgodnie z przyjętą zasada, to będzie ona zawierać wszystkie cyfry pewne, łącznie z ostatnią.

Zgodnie z ustaleniem, że błąd graniczny charakteryzuje się odpowiednim zapisem, nie wolno dopisywać zbędnych cyfr, które mogłoby sugerować większą dokładność niż faktycznie istniejąca. Pisząc np. l = 15 km, stwierdza się tym samym, że l jest liczbą przybliżoną o błędzie krańcowym
l = 0,5 km.

Jeżeli jednak napisze się l = 15 000 m, to błąd krańcowy wynosi
l = 0,5 m. Widzimy, że dwie formalnie równe wartości: l = 15 km i l = 15 000 m,zapisane jako liczby przybliżone, mają różne błędy krańcowe. Dlatego też liczbę a = 314,657 48, o której wiemy, że ma tylko 5 początkowych cyfr pewnych, zapiszemy w postaci a = 314,66 lub a = 31 46610-2. Podobnie gdy liczba całkowita b = 165 784 645 ma sześć początkowych cyfr pewnych, zapiszemy ją następująco:

b = 165 784103 . Jej błąd krańcowy jest równy
b = 0,5103.

Zamiast mówić „liczba ma n poczatkowych cyfr pewnych”, używa się zwrotu „liczba ma n cyfr znaczących pewnych”.

Liczby przybliżone charakteryzuje się ilością cyfr znaczących. Cyframi znaczącymi są wszystkie cyfry liczb oprócz zer położonych na lewo od pierwszej różnej od zera cyfry.

Podane niżej liczby mają następujące ilości cyfr znaczących:235,56 - 5 cyfr znaczących,

1 357,00 - 6 cyfr znaczących,

0,467 - 3 cyfr znaczących,

500,014 - 6 cyfr znaczących,

6 000,000 - 7 cyfr znaczących,

0,005 - 1 cyfra znacząca.

Zera występujace na końcu liczb mogą mieć dwojakie znaczenie: mogą wskazywać rząd wielkości liczby oraz charakteryzować jej dokładność wyrażoną ilością cyfr znaczących.

Dla włściwej interpretacji ustalono konwencję specjalnego zapisu liczb przybliżonych. Dzięki niej można określić dokładność bez osobnego podawania błędu czy ilości cyfr dokładnych. Napisana liczba 8,456 ma cztery cyfry dokładne. Jeżeli liczba 120 000 ma tylko trzy cyfry dokładne, to niedokładne zera zastępuje się odpowiednią potegą liczby 10, pisząc 120103 lub też 1,20105, a dla zaznaczenia, że liczba 0,2 ma cztery cyfry dokładne, pisząc 0,2000.

Konwencja powyższa nie dotyczy jednak obliczeń pomocniczych, gdzie nieraz wpisuje się więcej cyfr znaczących danej liczby przybliżonej, niż ma ona dokładnych, aby nie powiększać błędów wynikających z działań przybliżonych. Te zapasowe cyfry, maskujace właściwą dokładność liczb występujących w rachunku, nie powinny jednak wprowadzać liczącego w błąd. W tym celu zaleca się zapisywać cyfry zapasowe mniejszym pismem.

1.2.2. Zaokrąglanie liczb przybliżonych

Operując liczbami przybliżonymi, spotykamy się często z koniecznością ich zaokrąglania w przypadkach, gdy dokładność danych lub obliczanych liczb przewyższa potrzebną nam dokładność. Liczby przybliżone zaokrąglamy przestrzegając zasady, by błąd krańcowy nie przekraczał połowy jednostki ostatniego miejsca liczby zaokrąglonej. W myśl tego:

a) Ostatnią, pozostawioną cyfrę zwiększamy o 1, gdy pierwsza z odrzuconych cyfr jest większa niż 5.

b) Ostatnią cyfrę pozostawiamy bez zmiany, gdy pierwsza z odrzuconych cyfr jest mniejsza niż 5.

c) Jeżeli pierwsza z odrzuconych cyfr jest równa 5 i nie następują po niej inne cyfry niż zera, ostatnią cyfrę, gdy jest nieparzysta, zwiększamy o jedność, gdy jest parzysta - pozostawiamy bez zmiany.

d) Jeżeli pierwsza z odrzuconych cyfr jest równa 5, lecz następuje po niej co najmniej jedna cyfra inna niż zero, ostatnią pozostawioną cyfrę zwiększa się o jednostkę.

Niekiedy, w celu prawidłowego dalszego zaokrąglenia liczby przybliżonej, kończącej się cyfrą 5, stawia się nad nią kropkę w przypadku zaokrąglania z niedomiarem lub kreskę w przypadku zaokrąglenia z nadmiarem.

Podane niżej liczby są zapisane w myśl przedstawionych zasad:

12,678 45 12,68

136,453 42 136,453

40,500 40

41,500 42

42,501 43

1.2.3.Ocena dokładności funkcji liczb przybliżonych

Mierzone bezpośrednio wielkości fizyczne służą nam zazwyczaj do obliczania innych wielkości. Tak na przykład dla obliczenia wspołrzędnych punktów mierzy się długości boków i kąty. Wyniki rachunków geodezyjnych, wykonywane na

liczbach przybliżonych, lub ogólniej - wartości funkcji argumentów przybliżonych są także przybliżone. Zagadnienie sprowadza się do obliczenia błędu wartości znanej funkcji, gdy znane są błędy jej argumentów.

Spośród wielu metod wyróżnia się:

a) metodę podwójnego obliczania,

b) metodę różniczki zupełnej,

c) prawo przenoszenia się błędów,

d) metodę wielocyfrowości.

A. Metoda podwójnego obliczania

W tej metodzie oblicza się dwukrotnie zadaną wartość funkcji F = F (x,y,...,s) podstawiając do niej takie liczby przybliżone, by wraz ze znanym błędem przybliżenia (x
x), (y
y),...,(s
s) otrzymać maksymalną oraz minimalną wartość funkcji.

(1.3)

B. Metoda różniczki zupełnej

Metoda ta wyraża się wzorem rachunku różniczkowego

(1.4)

gdzie przy założeniu, że
F = dF oraz
x = dx, itp., wzór (1.4) jest wtedy różniczką zupełną funkcji F = F (x,y,...,s).

C. Prawo przenoszenia sie błędów

Obliczanie błędu funkcji F (x,y,...,s), oparte o prawo przenoszenia się błędów, scharakteryzowane jest wzorem

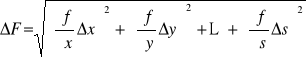
(1.5)

którego pochodzenie oraz właściwą interpretację pozna czytelnik w rozdziale 1.4.

D. Metoda wielocyfrowości - reguły Kryłowa-Bradisa

W odróżnieniu od omówionych metod, metoda wielocyfrowości jest metodą przybliżoną. Metody ścisłe są uciążliwe rachunkowo oraz nie uwzględniają prawdopodobieństwa występowania poszczególnych błędów. Z tych też względów nie nadają się do praktycznego zastosowania. Metoda wielocyfrowości nie określa wprawdzie ściśle błędów mogących wystąpić w rachunku, pozwala jednak na szybkie zorientowanie się, jakiego rzędu wielkości błędów możemy się spodziewać. Właściwego ujęcia tej metody oraz trafnego zebrania zasad obliczeń za pomocą liczb przybliżonych dokonali matematycy - Kryłow i Bradis. Poniżej podane są reguły rachunkowe Kryłowa-Bradisa dla typowych działań:

1. Przy dodawaniu i odejmowaniu liczb przybliżonych należy w wyniku zachować tyle miejsc dziesiętnych, ile ich zawiera liczba o najmniejszej ilości miejsc dziesiętnych.

Uwaga. Miejscami dziesiętnymi liczby nazywamy miejsca położone na prawo od przecinka dziesiętnego.

2. Przy mnożeniu i dzieleniu należy w wyniku zachować tyle cyfr znaczących, ile ich zawiera liczba przybliżona o najmniejszej ilości cyfr znaczących.

Uwaga. Cyframi znaczącymi liczby nazywamy wszystkie jej cyfry, z wyjątkiem zer służących wyłącznie do określania położenia przecinka dziesiętnego.

3. Przy podnoszeniu do kwadratu i sześcianu należy w wyniku zachować tyle cyfr znacących, ile ich zawiera liczba potęgowana.

Uwaga. Ostatnia cyfra potęgi, kwadratu, a zwłaszcza sześcianu jest przy tym mniej pewna od ostatniej cyfry potęgowanej liczby.

4. Przy wyciąganiu pierwiastka kwadratowego i sześciennego w wyniku należy zachować tyle cyfr znaczących, ile ich zawiera pierwiastkowana liczba.

Uwaga. Ostatnia cyfra pierwiastka, w szczególności sześciennego, będzie przy tym pewniejsza od ostatniej cyfry liczby pierwiastkowej.

5. Przy obliczaniu pośrednich wyników rachunku należy brać zawsze o jedną cyfrę więcej, niż to wskazują powyższe zasady.

Uwaga. W rezultacie końcowym tę zapasową cyfrę odrzucamy. Zaleca się ją pisać drobniejszym pismem.

6. Jeżeli niektóre dane zawierają więcej dziesiętnych znaków (w działaniach pierwszego stopnia) lub więcej cyfr znaczących (w działaniach drugiego lub trzeciego stopnia) niż pozostałe, należy je przede wszystkim zaokrąglić, zachowując jedną, zbędną według reguł, cyfrę.

7. Jeżeli dane wyjściowe można brać do rachunku z dowolną dokładnością, wówczas celem otrzymania wyniku o k cyfrach, należy brać dane z taką ilością cyfr znaczących, która zgodnie z regułami 1-4 daje (k+1) cyfr wyniku.

Powyższe reguły oparte są na następującej zasadzie ogólnej: Liczbę przybliżoną należy pisać tak, by wszystkie jej cyfry znaczące, z wyjatkiem ostatniej, były ścisłe. Błąd ostatniej cyfry nie powinien przekraczać średnio jednostki. PRZYKŁAD 1. Obliczyć wartość sumy

S = 12,763 425+6,758+123,425+78,293 62+18,61+21,3625

Zgodnie z regułą 6, przed wykonaniem działania zaokrąglamy liczby pozostawiając 3 miejsca po przecinku, gdyż najmniejsza ilość miejsc dziesiętnych występuje w składniku przedostatnim i wynosi dwa. Po zaokrągleniu sumujemy, otrzymując

S = 12,763+6,758+123,425+78,294+18,61+21,362

Jeżeli uzyskany wynik będzie użyty do dalszych rachunków, to zapiszemy go w postaci S = 261,212 (reguła 5), jeżeli natomiast jest on rezultatem końcowym, to zgodnie z regułą 1 pozostawimy w nim dwa miejsca dziesiętne pisząc S = 261,21. PRZYKŁAD 2. Obliczyć wartość iloczynu

I = 2,63764,298,780,375840,23.

Zgodnie z regułą 6 zaokrąglimy czynniki, pozostawiając w każdym, z wyjątkiem ostatniego, trzy cyfry znaczące. (Ilość cyfr czynnika zawierającego najmniej cyfr znaczących wynosi dwa). Otrzymamy I = 2,6464,298,80,3760,23. Wykonując działania i pamiętając o regule 5, będziemy mieli kolejno

I = 16998,80,3760,23

I = (167102)0,3760,23

I = 62,80,23102

I = 14,4102

Jeżeli wynik stanowi pośrednie stadium rachunku, zapisujemy go w postaci I = 14,4102 . Gdy jest to wynik końcowy, będzie I = 14102.

PRZYKŁAD 3. Obliczając kwadrat (96,4)2 , zapiszemy wynik w postaci 9293 lub 929102 (reguła 3), w zależności od tego, czy liczba bierze udział w dalszym rachunku, czy stanowi wynik końcowy.

PRZYKŁAD 4. Sześcian (0,8935)3 obliczymy, korzystając z reguł 5 i 3. Będzie kolejno (0,8935)3 = 0.798340,8935 = 0,71332 lub 0,7133.

PRZYKŁAD 5. Obliczając wartość pierwiastka kwardatowego z liczby 62,873, zachowamy w wyniku 6 lub 5 cyfr znaczących (reguły: 4 i 5). Będzie więc

7,92925 lub 7,9292

PRZYKŁAD 6. Obliczając wartość wyrażenia

Licznik ma 3 cyfry znaczące pewne, przy czym pozostawiono dodatkową czwartą, gdyż jest to pośredni wynik rachunku L = 3,6+10,68+13,73 = 28,01. Mianownik ma 4 cyfry znaczące pewne, z piątą cyfrą pozostawioną z tych samych względów M = 1,654+6,82+15,261 =23,735. Iloraz będzie więc miał 3 cyfry znaczące pewne, przy czym działania przeprowadzimy na liczbach czterocyfrowych. Ponieważ pierwiastek z liczby mającej trzy cyfry znaczące pewne będzie miał 3 cyfry znaczące pewne, otrzymamy kolejno

lub 1,09

PRZYKŁAD 7. Wartość wyrażenia

obliczamy, stosując poznane reguły do kolejno wykonywanych działań. Otrzymamy

SL = 0,36+128,542 = 128,902

SM = 0,3+123.32+902,8 = 1026,42

lub 5,0

Czasem rezygnuje się ze ścisłego przestrzegania reguł Kryłowa-Bradisa, by zachować w wynikach pośrednich stale tę samą ilość miejsc dziesiętnych, która jest zwykle większa od podanej przez wyżej wymienione reguły. Operowanie liczbami zawierającymi jednakową ilość znaków dziesiętnych znacznie ułatwia obliczenia i zmniejsza możliwość popełnienia błędów rachunkowych.

2

---