Wydział Geodezji i Gospodarki Przestrzennej Olsztyn, 23.05.2011r.

Kierunek: Geodezja i Kartografia

Specjalność: Geodezja i Geoinformatyka

PRACE ZIEMNE

Wpływ ukształtowanie powierzchni terenu na dokładność określenia objętości

Piotr Płókarz

Gr. 2, Rok III

Błędy określenia objętości gruntów.

Można wyróżnić dwa podstawowe źródła błędów określenia objętości:

1. błędy pomiarów i opracowań map, na które składają się:

1. błąd odwzorowania terenu

2. błąd pomiaru rzeźby terenu

3. błąd opracowania mapy warstwicowej

2. błędy obliczania objętości, wynikające z przyjętego sposobu obliczeń

Błąd odwzorowania terenu

Powierzchni terenu nie można odwzorować wiernie (izometrycznie). Każdy pomiar rzeźby terenu stanowi przybliżenia powierzchni terenu powierzchnią topograficzną, czyli powierzchnią określoną zbiorem punktów o znanych współrzędnych w przyjętym układzie odniesienia. Geodeta, dokonując pomiaru powierzchni terenu dzieli ją na szereg płaszczyzn, najczęściej trójkątnych, przez wyznaczenie współrzędnych wierzchołków figur. W rzeczywistości pomiędzy trzema punktami tworzącymi płaszczyznę rozpięty jest pewien płat powierzchni terenu o nieregularnej krzywiźnie. Punkty powierzchni terenu mogą względem danej płaszczyzny przyjmować różne położenia:

1. wszystkie nad płaszczyzną (powierzchnia wypukła)

2. wszystkie pod płaszczyzną (powierzchnia wklęsła)

3. 
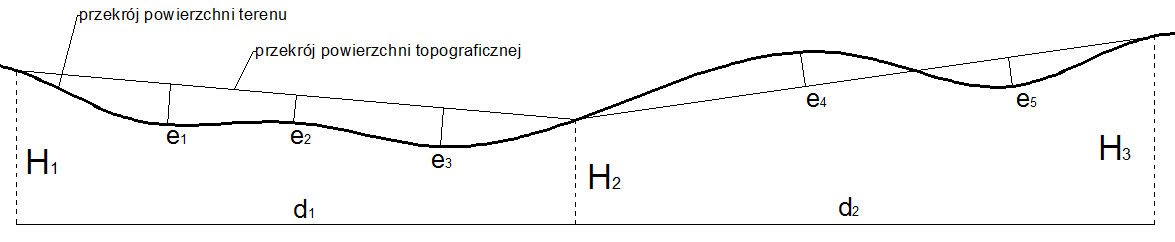
   cześć punktów nad, część pod, a wobec tego część również na płaszczyźnie

Odległości e_i powierzchni terenu zmieniają się od 0 do e_max , gdzie e_max - największa odległość pomiędzy powierzchnią terenu a daną płaszczyzną.

Ze względu na nieskończoną ilość punktów na powierzchni, średnią odległością e₀ będzie wartość oczekiwana E(e_i), a zatem objętość bryły V_i, utworzonej przez płat powierzchni terenu i daną płaszczyznę pola S_i będzie:

V_i = E(e_i)S_i

W rozpatrywanym punkcie odległości e_i są błędami prawdziwymi odwzorowania terenu i jak wiadomo mogą być z dostatecznym przybliżeniem określone na drodze pomiaru. Z uwagi na skończoną liczbę punktów powierzchni, w których możemy dokonać pomiaru, wartość oczekiwaną E(e_i) zastąpimy średnim błędem odwzorowania terenu:

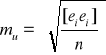
gdzie e_i - odległość pomiędzy powierzchnią terenu a płaszczyzną powierzchni topograficznej, pomierzona w punkcie i z dokładnością umożliwiającą uznać ją za błąd prawdziwy; n - liczba pomierzonych odległości.

Wpływ błędu odwzorowania terenu na dokładność obliczenia objętości gruntu będzie zależna od charakteru terenu. Jeżeli teren jest zróżnicowany pod względem ukształtowania powierzchni, tzn. gdy wymienione pod (a), (b), (c) położenia powierzchni terenu względem płaszczyzny topograficznej występują w przybliżeniu z jednakową częstotliwością na całym obszarze objętym robotami ziemnymi, wówczas ze względu na jednakowe prawdopodobieństwo wystąpienia dodatnich i ujemnych błędów odwzorowania terenu e_i można napisać:

gdzie:

m_Vz - wpływ błędu odwzorowania terenu na dokładność obliczenia objętości gruntu

m_z - średni błąd odwzorowania terenu

S₀ - pole średniego trójkąta utworzonego przez punkty pomiaru rzeźby terenu

n - liczba trójkątów na obszarze o powierzchni S

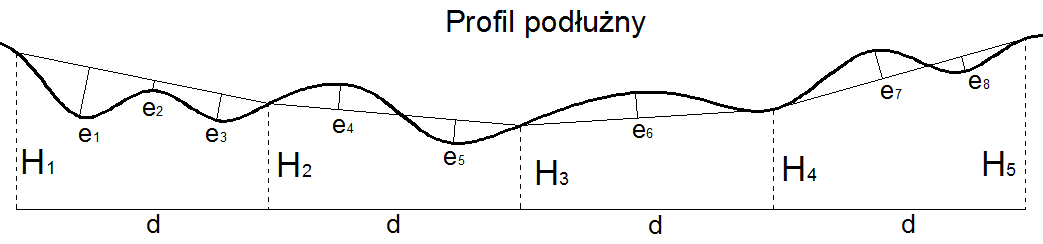
Praktyczne zastosowanie tej metody można przedstawić za pomocą pomiaru wgłębienia terenu. Kiedy to dla lepszego odzwierciedlenia objętości możemy zbudować siatkę kwadratów o długości boku np. 20m, a w miejscach charakterystycznych dla mierzonego obszaru dodatkowo dokonujemy odczytu. Zwiększy to dokładność odwzorowania terenu, a zarazem zmniejszy błąd pomiaru rzeźby terenu.

gdzie :

d - długość boku siatki kwadratów
H_i - wysokość na punktach węzłowych siatki

e_i - odległość między powierzchnią terenu a daną płaszczyzną w charakterystycznych punktach terenu

---