Ostatnio mówiliśmy o kryptografii klucza publicznego i skończyliśmy na kryptosystemie RSA. Dziś natomiast zajmiemy się zastosowaniem kryptosystemu klucza publicznego do realizacji usług uwierzytelniania. Załóżmy, że strona A uwierzytelnia się (potwierdza swoją tożsamość wobec strony B). Strona A ma swój klucz prywatny
. Z kolei strona B ma certyfikowany klucz publiczny
strony A. Popatrzmy najpierw jak wygląda generacja dowodu tożsamości przez stronę A. Odbywa się to w dwóch punktach:

1. Strona A sporzadza sensowną wiadomość jawną M.

2. Strona A przekształca, czyli szyfruje M swoim kluczem prywatnym
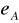
   , czyli oblicza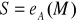
   i wysyła to S do strony B.

To S nazywa się tutaj podpisem M z odtwarzaniem wiadomości wykonywanym przez A. I tutaj nastepuje w dwóch krokach weryfikacja tożsamości A przez stronę B. I tak:

1. Strona B stosuje klucz publiczny
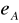
   strony A do przekształcenia, czyli odszyfrowania wiadomości. Robi to w ten sposób: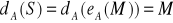
   

2. Jeśli wiadomość M jest sensowna, to potwierdza to tożsamość A, a konkretnie potwierdza to, że A ma właściwy klucz prywatny. Została przy tym odtworzona wiadomość M.

I to tyle jeśli chodzi o kryptografie klucza publicznego. Kolejnym naszym tematem będzie intergralność i jednokierunkowe funkcje skrótu. Na początek powiemy nieco o intergralności danych. Wymiana danych odbywa się w taki sposób, jak to pokazano na rysunku:

Strona A wysyła do strony B jakąś wiadomość M wraz z jej skrótem, czyli cyfrowym odciskiem oznaczanym h(M). Strona B po otrzymanu wiadomości M' (zakładamy, że M mogła ulec zmianie) oblicza skrót h(M'), a następnie sprawdza, czy h(M') = h(M). Jeśli tak, to wówczas wnioskuje, że M' = M, a jeśli nie to wnioskuje, że M' nie jest równe M (Oznacza to, że wiadomośc M uległa zmianie podczas transmisji). Wnioskowanie oparte jest na własnościach zastosowanej funkcji skrótu h, która służy do sprawdzania intergralności danych. Teraz kilka słów o jednokierunkowych funkcjach skrótu. Jednokierunkową funkcję skrótu oznaczamy wzorem
, gdzie:

to ciągi bitowe dowolnej długości (zbiór wszystkich wiadomości)

to z kolei ciągi bitowe o długości n bitów, gdzie n jest długością skrótu.

W praktyce zwykle n wynosi 128, 160, lub 256 bitów. Teraz omówmy cztery podstawowe warunki nakładane na funkcje skrótu:

1. Obliczanie skrótu h(x) dla
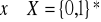
   jest efektywne (złożoność wielomianowa).

2. Dla
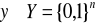
   trudne obliczeniowo jest znalezienie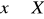
   takiego, że h(x) = y (złożoność O(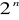
   )).

3. Dla
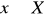
   trudne obliczeniowo jest znalezienie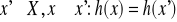
   (złożoność O(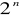
   )).

4. Trudno obliczeniowo jest znaleźć
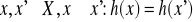
   , czyli tak zwana

odporność na kolizje(złożoność O(
) - na podstawie paradoksu dnia urodzin).

Funckje skrótu uwazamy za złamaną, jeśli w jednym z punktów - 2, 3, lub 4, wykorzystując budowę wewnętrzną funkcji skrótu, uzyskmy złożoność mniejszą niż wskazana wynikająca z warunków ogólnych. Oto, jakie mamy najczęściej stosowane jednokierunkowe funkcje skrótu:

1. MD4 - skrót 128 bitów. Złamana, aktualnie nie stosowana.

2. MD5 - skrót 128 bitów. Złamana ze względu na znajdowanie kolizji. Była powszechnie stosowana w protokole internetowym SSL.

3. SHA 1 - skrót 160 bitów. Standard USA. Występuje w standardzie podpisu cyfrowego. Miał jednak miejsce atak terrorystyczny na znajdowanie kolizji o zlożoności O(
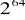
   ) dlatego ogłoszony został przez NIST konkurs na opracowanie nowych funkcji skrótu.

---