Na dzisiejszych zajęcich powiemy o równaniach różniczkowych zwyczajnych pierwszego rzędu. I na początek nieco przypomnienia. Każdy związek pomiędzy funkcją, jej pochodną izmienną x wielokrotną, czyli F(y, y', x) = 0 jest równaniem różniczkowym zwyczajnym rzędu I. Równanie to można zapisać w postaci: y' = f(x, y).

Jest kilka rodzajów takich równań. Na poczatek powiemy sobie o pierwszym z nich - o równaniu różniczkowym o zmiennych rozdzielonych. Tównanie to określone jest wzorem:

Popatrzmy na przykład:

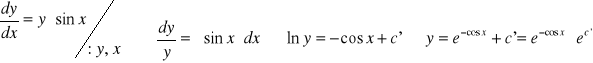
Przyrównując c do
nasze równanie przyjmie postać
i jest to całka ogólna równania różniczkowego. Sprawdźmy jeszcze, czy rachunek jest dobry:

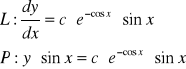
A więc się zgadza. Rozpatrzmy jeszcze taki przykład:
. To nam dalej daje
. I jeszcze kilka przykładów do wykonania w domu:

A teraz przejdziemy do drugiego równania - równania różniczkowego liniowego rzędu I. Jest ono określone wzorem:

Dla obliczenia tego równania musza zostać podjęte trzy kroki. Pierwszy krok to obliczenie CORLJ, czyli całki ogólnej równania liniowego jednorodnego
. Drugi krok to obliczenie CSRLN, czyli calki szczególnej równania liniowego niejednorodnego, która powstaje przez uzmiennienie
stałej c w CORLJ. I ostatni krok to obliczenie CORLN, czyli calki ogólnej równania liniowego niejednorodnego będącego sumą CORLJ i CSRLN. Popatrzmy teraz na przykład, jak to się liczy.

Rozwiążmy przykład
.

1. Najpierw liczymy CORLJ

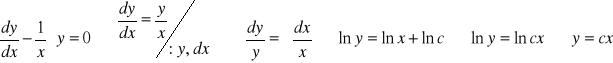
2. Kolejny krok to obliczenie CSRLN. CSRLN poszukujemy w postaci y = c(x) * x. Podstawiając y do (*) otrzymuję:

Zatem nasze CSRLN wynosi ostatecznie
.

3. I teraz CORLN otrzymujemy z wysumowania, co daje nam
   .

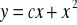
Przejdźmy teraz do kolejnego przykładu, a mianowicie

1. CORLJ:

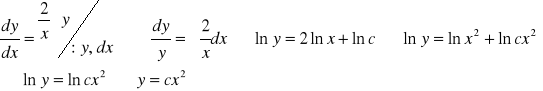
2. CSRLN poszukujemy w postaci
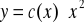
   . Podstawiając y do (*) optrzymujemy:

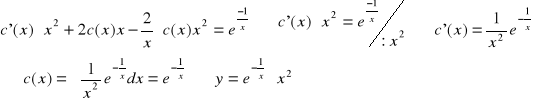
3. CORLN:
   

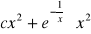
Teraz kilka zadań do rozwiązania w domu (przykłady analogiczne do powyższych):

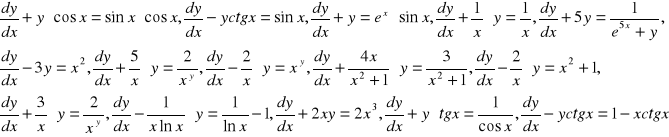
My natomiast z powyższych przykładów rozwiążemy jeden. Wykonajmy przykład ostatni. I tak mamy:

1. CORLJ

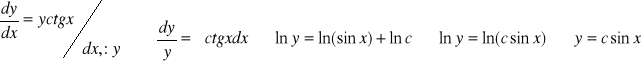
2. CSRLN poszukujemy w postaci
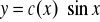
   . Podstawiając y do (*) otrzymuję:

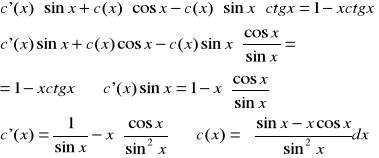
3. CORLN:

c może być dowolna, dlatego c = lnc

---