Dziś kontynuować będziemy temat ekstremów warunkowych. Mamy daną funkcję ![]()
z poprzednich ćwiczeń, oraz warunek dany wzorem ![]()
. Należy znaleźć ekstremum warunkowe. Najpierw rysunek tej sytuacji:
I teraz nieco przypomnienia. Naszym zadaniem będzie znalezienie ekstremum warunkowego w ![]()
pod warunkiem ![]()
. Zawsze na początek buduje się funkcję Lagreange'a:
![]()
Następnie szukamy jej punktów stacjonarnych ![]()
dla ![]()
rozwiązując następujący układ równań:
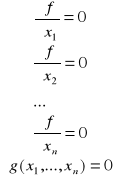
Na koniec sprawdzamy warunek dostateczny. Warunkiem dostatecznym jest, by w punkcie ![]()
było minimum (maksimum) warunkowe funkcji gdy wszystkie wyznaczniki główne ![]()
, czyli hesjanu obrzeżonego równego:
Spełniały warunki: ![]()
. No i na podstawie tych definicji rozwiążmy nasz przykład zaczynając od funkcji Lagrange'a. W naszym przypadku będzie to ![]()
. A zatem: ![]()
. I teraz budujemy dla tej funkcji układ stacjonarny:
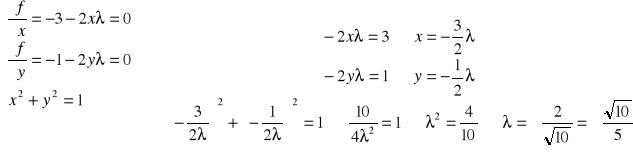
Z tego dla ![]()
mamy ![]()
. I stąd właśnie wynika pierwszy punkt stacjonarny ![]()
. Z kolei dla ![]()
mamy drugi punkt stacjonarny ![]()
. Stąd dalej budujemy hesjan obrzeżony:
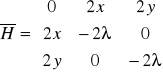
.
I teraz liczę dla pierwszego z puktów stacjonarnych wyznacznik 2x2 i 3x3 podstawiając współrzędne punktu do hesjanu:
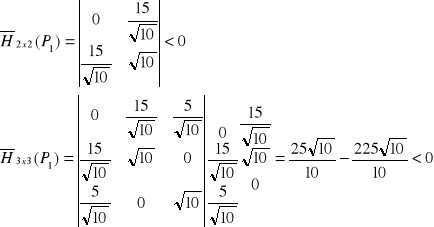
Obydwa eyznaczniki jak widać sa ujemne. St ąd zniosek, że funkcja w punkcie ![]()
ma minimum lokalne przy warunku ![]()
. Dla drugiego punktu sprawdzamy identycznie.
Teraz przejdźmy do zadania kolejnego. Należy obliczyc ekstremum warunkowe funkcji ![]()
przy warunku ![]()
. Oto rysunek całej sytuacji, który wygląda mniej więcej tak:
No i wyznaczamy funkcję Lagrange'a: ![]()
. Nastepnie buduje układ stacjonarny:
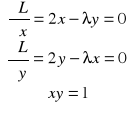
Z pierwszej części układu wynika, że ![]()
. I teraz to, co otrzymałem podstawiam za x do drugiej części układu. I mam:
![]()
Dla ![]()
ten układ ma się tak:
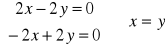
. Z podstawienia mamy, że ![]()
. Stąd wychodza nam dwa punkty stacjonarne (minimum sprawdzimy dla pierwszego): ![]()
. I tak mamy hesjan:
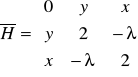
No i liczymy wyznacznik hesjana 2x2 i 3x3:
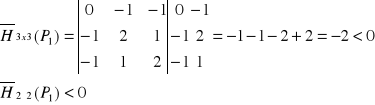
Stąd wnioskujemy, że w punkcie P jeden funkcja ma minimum przy zadanym warunku. No i na koniec to samo zadanie z przykładami do obliczenia w domu. Należy wyznaczyć ekstremum warunkowe dla:
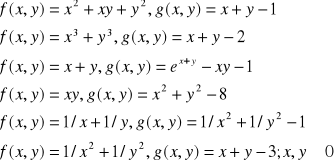
Wyszukiwarka
Podobne podstrony:
Z Ćwiczenia 26.04.2008, Programowanie
Z Ćwiczenia 20.04.2008, Zajęcia, II semestr 2008, Teoria informacji i kodowania
Z Ćwiczenia 19.04.2008, Zajęcia, II semestr 2008, Algorytmy i struktury danych
Z Ćwiczenia 05.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Ćwiczenia 06.04.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Z Ćwiczenia 27.04.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Z Wykład 26.04.2008, Zajęcia, II semestr 2008, Rachunek prawdopodobieństwa
Z Ćwiczenia 29.03.2008, Zajęcia, II semestr 2008, Wstęp do kryptologii
Z Ćwiczenia 15.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 19.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Ćwiczenia 01.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 06.04.2008, Zajęcia, II semestr 2008, Rachunek prawdopodobieństwa
Z Wykład 05.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Ćwiczenia 01.06.2008, Zajęcia, II semestr 2008, Rachunek prawdopodobieństwa
Z Ćwiczenia 17.05.2008, Zajęcia, II semestr 2008, Teoretyczne podst. informatyki
Z Wykład 20.04.2008, Zajęcia, II semestr 2008, Algorytmy i struktury danych
Z Ćwiczenia 14.06.2008, Zajęcia, II semestr 2008, Algorytmy i struktury danych
więcej podobnych podstron