18.8 Moment magnetyczny atomu i elektronu.

Moment magnetyczny jest zawsze przeciwnie skierowany do momentu pędu.

Moment magnetyczny  :

 ;   

,      
.

Moment magnetyczny w atomie wodoru jest wielkością skwantowaną.

Oznaczenia:
b - moment pędu;
h - stała Plantha;
e - ładunek elementarny;
m_e - masa elektronu;
n - numer orbity;
m - moment magnetyczny;
 - moment magnetyczny Bohra (wielkość stała)

18.9 Spinowy moment magnetyczny.

Jest związany z ruchem elektronu wokół własnej osi.


;   


spinowy moment magnetyczny:
 


Spinowy moment magnetyczny jest odpowiedzialny za właściwości magnetyczne materii (zob.pkt. 22.11)

Oznaczenia:
h - stała Plantha;
e - ładunek elementarny;
m_e - masa elektronu;
m -spinowy  moment magnetyczny;
s - spin

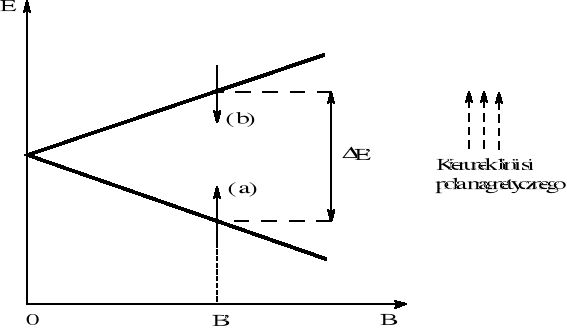
Jądra atomowe niektórych pierwiastków mają moment pędu, zwany spinem, w związku z czym wykazują właściwości magnetyczne. Poglądowo można przyjąć, że takie jądra wykonują ruch wirowy i wirowanie ładunku odpowiedzialne jest za ich magnetyczność. Jądra te charakteryzują się niezerową wartością liczby spinowej I. Jeśli tego rodzaju jądro umieści się w stałym, jednorodnym polu magnetycznym o indukcji B, wektor spinu przyjmie w przestrzeni tylko określone położenia, a o układzie powiemy, że jest skwantowany. Liczbę tych położeń określa wzór N=2I+1, gdzie I oznacza liczbę spinową. Na przykład proton ¹H, a także izotop węgla ¹³C (jego naturalna zawartość wynosi ok. 1%, natomiast dominującym w przyrodzie izotopem węgla jest ¹²C), mają liczby spinowe równe ½, więc ich spiny zajmują w stałym zewnętrznym polu magnetycznym dwa różne położenia, ponieważ 2×½+1=2. Położenia te można opisać jako (a) - równoległe, (b) - antyrównoległe do linii sił pola, przy czym różnica energii między położeniami (a) i (b) pojawia się dopiero po przyłożeniu pola i jest proporcjonalna do jego indukcji B

Z reguł mechaniki kwantowej wynika, że zawsze występuje niewielki nadmiar jąder w niższym stanie energetycznym, a więc po zorientowaniu spinów w polu powstaje wypadkowy makroskopowy moment magnetyczny układu badanych jąder, który można opisać wektorem magnetyzacji, równoległym do linii sił pola B. Wektor ten wykonuje ruch wirowy wokół kierunku linii sił pola B z częstością proporcjonalną do wartości wektora indukcji B. W celu przeprowadzenia pomiaru metodą NMR impulsowo przykłada się dodatkowe, zmienne pole elektromagnetyczne, którego częstość _g zrównuje się z częstością wirowania wektora magnetyzacji, reprezentującego badany rodzaj jąder. Gdy te częstości są równe, ma miejsce zjawisko rezonansu, i wtedy spełnione są równania

h_g = ΔE' = E_b - E_a [1]

_g = γB·h/2Π [2]

gdzie h oznacza stałą Plancka, a γ jest współczynnikiem magnetogirycznym. Ponieważ pasmo impulsowe jest wystarczająco szerokie (rzędu kiloherców), jednoczesnemu wzbudzeniu ulegną wszystkie jądra analizowanego pierwiastka, znajdujące się w różnych otoczeniach, a więc wchodzące w rezonans przy nieco różnych natężeniach pola. Częstość generatora zmiennego pola elektromagnetycznego sięga kilkuset megaherców, np. w nowoczesnych aparatach przy badaniu protonów stosuje się częstości 500-800 MHz.

W wyniku przyłożonego impulsu zmiennego pola elektromagnetycznego wektor magnetyzacji ulega wychyleniu, a następnie powraca do stanu równowagi dzięki procesom relaksacji, polegającym na bezemisyjnym oddawaniu przez jądra nadmiaru energii do otoczenia. Tzw. relaksacja podłużna, charakteryzowana przez czas T₁, polega na wymianie energii spin-sieć, natomiast relaksacja poprzeczna, opisana czasem T₂, dotyczy transferu energii między spinami pobliskich jąder. Procesy relaksacji odtwarzają pewien nadmiar jąder na niższym poziomie, co umożliwia pomiar metodą NMR. Detektor wykrywa emisję energii jąder po ustaniu wzbudzającego impulsu, wyrażoną przez zmniejszanie się wychylenia wektora magnetyzacji w płaszczyźnie xy, a rejestrowany zanikający sygnał zwany jest sygnałem swobodnej precesji (FID). Ten sygnał zawiera informację dotyczącą wszystkich badanych jąder układu, a jego analizę pod kątem wyodrębnienia danych o jądrach znajdujących się w różnych otoczeniach magnetycznych, czyli uzyskania widma NMR, przeprowadza się metodą transformacji Fouriera

Larmora precesja, larmorowska precesja, ruch precesyjny orbitalnego momentu pędu i związanego z nim momentu magnetycznego elektronu wokół kierunku zewnętrznego pola magnetycznego o indukcji B, zachodzący z prędkością kątową ϖ=eB/2m_ec, gdzie e i m_e - ładunek i masa elektronu, c - prędkość światła w próżni.

Jest to częstość wirowania momentu magnetycznego, który ustawiony pod kątem α do pola magnetycznego precesuje wokół pola.

a) częstość kołowa (VIII.2.1a) b) częstość liniowa (VIII.2.1b) Z (VIII.2.1a) wynika, że: oraz że

Rys. 1. Rozszczepienie poziomów energetycznych jądra o spinie ½ w stałym polu magnetycznym.

---