POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI	SPRAWOZDANIE Z ĆWICZENIA NR 25 TEMAT : WYZNACZANIE WSPÓŁCZYNNIKA ROZSZERZALNOŚCI LINIOWEJ METODĄ ELEKTRYCZNĄ.
KRZYSZTOF JUNGOWSKI IZ rok II	DATA WYKONANIA : 8 . 11 .95 OCENA : ..............................

1. ROZSZERZALNOŚĆ CIEPLNA.

Zmiana objętości ciała pod wpływem zmiany temperatury. R.c. tłumaczy się wzrostem średniej odległości między cząsteczkami wskutek zwiększania się energii ruchu drgających cząsteczek. Ilościowo zjawisko r.c. charakteryzuje współczynnik rozszerzalności objętościowej a zdefiniowany przez związek :

ΔV = --> [Author:(null)] αV₀ ΔT

gdzie :

V₀ - objętość początkowa ciała

ΔV - zmiana objętości ciała spowodowana niezbyt dużą zmiana temperatury o ΔT przy ustalonej wartości ciśnienia.

W przypadku ciał stałych wprowadza się również współczynnik rozszerzalności liniowej λ zdefiniowany wzorem :

Δl = λl₀ ΔT

gdzie:

l₀ - długość początkowa

Δl - zmiana długości ciała spowaodowana niewielką zmianą temperatury o ΔT przy ustalonym ciśnieniu

Dla ciał izotropowych α = 3 λ ( izotropia - niezależność własności fizycznych substancji od kierunku)

Największą r.c. wykazują gazy, słabszą ciecze, a najsłabszą ciała stałe. Niektóre ciała (np. woda w temp. ok 4°C) mają w pewnych przedziałach temp. ujemne współczynniki rozszeżalności (tzw. anomalna rozszerzalność).

Przykładowe współczynniki liniowej rozszerzalności cieplnej:

ciało	λ ⋅10^-6 [K^-1]
ołów	28,3
srebro	19,0
miedź	16,6
platyna	9,0
inwar (64% Fe, 36% Ni)	1,6
krzem	2,5
szkło kwarcowe	0,4

przy danych warunkach :

p₀ = 101325 [Pa]; T₀ = 293,15 [K];

[według Encyklopedii Fizyki PWN 1991]

Wyznaczanie współczynnika rozszerzalności liniowej.

Badanie rozszerzalności cieplnej ciał stałych jest oparte zwykle na prawie opisującym zależność dłudości ciała od temperatury:

l_t = l₀ (1 + α ΔT)

gdzie :

l_t - długość ciała w temperaturze T;

t₀ - długość ciała w temperaturze T₀;

ΔT = T - T₀;

α - współczynnik rozszerzalności liniowej.

Przekształcenie ostatniego równania do postaci :

gdzie : l_t - l₀ = Δl;

daje wygodną formę do wyznaczenia α na podstawie zmierzonej zależności względnego wydłużenia od przyrostu temperatury. Wartość współczynnika rozszerzalności liniowej jest bowiem równa tangensowi kąta nachylenia krzywej na wykresie, przedstawiającym zależność wydłużenia względnego Δl/l₀ od przyrostu temperatury ΔT.

2. POMIARY I OBLICZENIA.

2.1 Przyrządy pomiarowe:

• cyfrowy miernik temperatury CMT 12 - podziałka 0,1 [° C] (na mierniku brak było tabliczki znamionowej);

• voltomierz analogowy klasy 1; trzy zakresy pomiarowe (15, 30, 75 [V]); podziałka - 75 dz;

w naszym przypadku używaliśmy zakresu 15[V], czyli czułość przyrządu :

(15/75) [V/dz] = 0.2 [V/dz]

2.2 Wartości początkowe i stałe:

l₀ = (1,110 ± 0,004) m =

= (1110 ± 4 ) mm (wartość podana);

t₀ = 21,5 [° C] (miernik)

= 22,0 [° C] (termometr)

W obliczeniach używać będziemy pierwszej watrości temperatury początkowej ze względu na zalecenie używania do pomiarów tych samych przyrządów.

2.3 Tabela pomiarowa:

	T [°C]	Δl [⋅0,01 mm]	ΔT [°C]	λ [⋅10^-6 °C^-1]	Δλ [⋅10^-6°C^-1]
1.	31,2	46	9,7	42,72	8,18
2.	43,1	71	11,9	53,75	2,85
3.	52,9	59	9,8	54,24	3,34
4.	65,7	71	12,8	41,27	9,63
5.	74,5	51	8,8	52,21	1,31
6.	84,5	56	10,0	50,45	0,45
7.	95,1	59	10,6	50,14	0,76
8.	105,2	67	10,1	59,76	8,86
9.	114,2	50	9,0	50,05	0,85
10.	124,5	56	10,3	48,98	1,92
11.	131,4	40	6,9	52,27	1,37
12.	140,1	45	8,7	46,60	4,30
13.	149,6	55	9,5	52,16	1,26
14.	135,5	-79	-14,1	50,48	0,42
15.	117,3	-98	-18,2	48,51	2,39
16.	104,9	-73	-12,4	53,04	2,14
17.	92,2	-69	-12,7	48,95	1,95
18.	75,0	-101	-17,2	52,90	2,00
19.	56,6	-105	-18,4	51,41	0,51
20.	39,1	-114	-17,5	58,69	7,79
21.	23,9	-85	-15,2	50,38	0,52
średnio:				50,90	3,04

Przykładowe obliczenia:

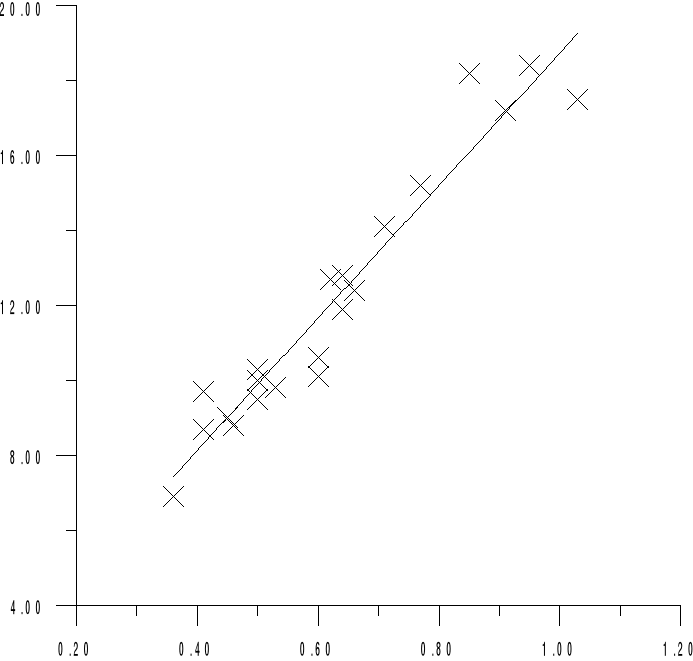
Na osi X zaznaczono iloraz

zas na osi Y ΔT [°C]

Współczynnik λ można obliczyć korzystając z wykresu, gdyż jest on równy tangensowi kąta nachylenia prostej (aproksymowanej) będącej wykresem zależności .

Zależność mierzonego napięcia od temperatury :

	U [⋅ 0,2 V]	T [°C]	τ [ V/°C]	Δτ [V/°C]
1.	7,0	31,2	0,045	0,001
2.	10,2	43,1	0,047	0,003
3.	12,8	52,9	0,048	0,004
4.	15,5	65,7	0,047	0,003
5.	17,7	74,5	0,048	0,004
6.	19,4	84,5	0,046	0,002
7.	21,5	95,1	0,045	0,001
8.	23,2	105,2	0,044	0
9.	24,8	114,2	0,043	0,001
10.	26,2	124,5	0,042	0,002
11.	27,6	131,4	0,042	0,002
12.	29,0	140,1	0,041	0,003
13.	30,3	149,6	0,041	0,003
14.	28,0	135,5	0,041	0,003
15.	25,0	117,3	0,043	0,001
16.	22,9	104,9	0,044	0
17.	20,5	92,2	0,044	0
18.	17,1	75,0	0,046	0,002
19.	13,0	56,6	0,046	0,002
20.	8,2	39,1	0,042	0,002
21.	-	23,9	-
średnio:			0,044	0,002

Przykładowe obliczenia:

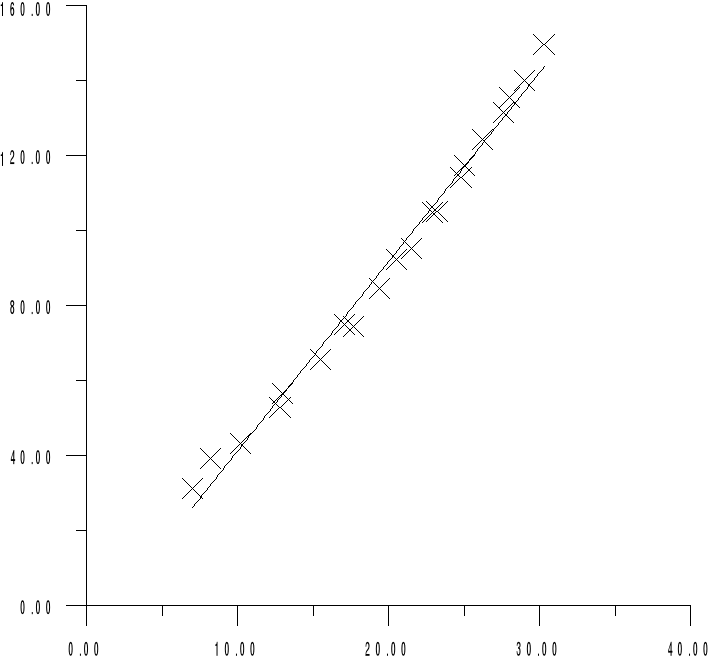
Na osi X przedstawiliśmy napięcie U [⋅0,2 V], zaś na osi Y temperaturę w [° C].

3. RACHUNEK BŁĘDÓW.

3.1 Błąd wyznacznia współczynnika rozszerzalności liniowej.

Metaoda różniczki zupełnej:

Obliczanie błędu:

δλ = Δλ /λ = 2,664 [%]

3.2 Błąd wyznaczania współczynnika τ.

δτ = Δτ/τ = 4,455 [%]

4. DYSKUSJA BŁĘDÓW.

Błędy wynikające z dokładności przyrządów są stosunkowo niewielkie, co wynika z dużej dokładności przyrządów. Mamy tu jednak do czynienia także z innymi błędami. Mierząc zmianę długości badanego drutu zerowaliśmy po każdym pomiarze miernik. Mogło to powodować błędy wynikające z niedokładności ustawienia wskazówki (za każdym razem kąt patrzenia na wskazówkę miernika mógł być inny, a więc wskazówka była inaczej ustawiana). Wpływ na zwiększenie błędu miało także to, że temperatura drutu bardzo wolno się stabilizowała i niektóre pomiary mogły zostać wykonane gdy temperatura jeszcze nie do końca się ustabilizowała. Temperatura w pomieszczeniu, w którym wykonywane było doświadczenie miała także wpływ na temperaturę drutu i zniekształcała pomiary. Z drugiej strony drut znajdował się w zamkniętej przestrzeni, co chroniło go przed prądami powietrza. Istotny wpływ na dokładność pomiarów miało także ustawienie strzałki ugięcia drutu (dokładne jej wyzerowanie miało zasadniczy wpływ na wartości odczytywane z miernika mierzącego wydłużenie drutu.

5. WNIOSKI.

Współczynnik rozszerzalności liniowej, który zmierzyliśmy nie odpowiada żadnemu współczynikowi rozszerzalności liniowej ciała stałego jaki mogę znależć w tablicach. Jednak dane znajdujące się w tablicach są dosyć ubogie na ten temat więc przypuszczam, że drut, którego współczynik rozszerzalności liniowej mierzyliśmy powstał ze specjalnego stopu.

7

---