Pomiar e/m metodą odchyleń w polu magnetycznym.

Na posiadającą ładunek elektryczny cząstkę, poruszającą się w polu elektrycznym i magnetycznym, działa siła , zwana siłą Lorentza, określona wzorem:

gdzie: q - ładunek cząstki, v - jej prędkość,

E - natężenie pola elektrycznego, B - indukcja magnetyczna.

Działanie obu wymienionych pól prowadzi w ogólnym przypadku do zmiany wektora prędkości - w polu elektrycznym może się zmieniać kierunek i wartość prędkości, natomiast w polu magnetycznym wartość prędkości pozostaje bez zmian (stała).

Badanie zachowania się cząstek naładowanych, jak np. elektronów, protonów, jonów dodatnich, w polach elektrycznym i magnetycznym pozwala wyznaczyć tzw. nabój właściwy, czyli stosunek q/m.

W celu określenia naboju właściwego elektronu posłużymy się lampą oscyloskopową z odchylaniem magnetycznym w kierunku Y. Pole magnetyczne wytwarzane jest w wyniku przepływu prądu przez uzwojenie umieszczone na zewnątrz lampy. Indukcja magnetyczna B jest proporcjonalna do natężenia prądu I
Współczynnik proporcjonalności c określamy empirycznie. Po wyjściu z obszaru pola magnetycznego elektrony biegną po linii prostej i w końcu uderzają w ekran fluorescencyjny wywołując jego świecenie. Warunek równowagi siły odchylającej w obszarze pola magnetycznego i siły bezwładności wyraża się równaniem

, gdzie R jest promieniem krzywizny toru.

Szukaną wielkość e/m możemy przedstawić w postaci

Prędkość możemy wyrazić napięciem U_a, przyrównując energię kinetyczną do pracy wykonywanej przez pole elektryczne na drodze między katodą i anodą

W ten sposób otrzymujemy:
Biorąc pod uwagę, że w warunkach doświadczenia y<< 1 oraz d << R możemy zapisać
Promień krzywizny R możemy zatem wyrazić w postaci
, gdzie: l - odległość ekranu lampy oscyloskopowej od środka cewki, d - średnica cewki odchylającej, y - odchylenie plamki na ekranie względem położenia przy B = 0.

Ostateczne wyrażenie, z którego możemy wyliczyć stosunek e/m:

Wielkość
została podana i wynosi ona
.

Błąd pomiaru natężenia prądu można obliczyć korzystając z klasy miernika:

= 35 mA (maksymalne wskazanie amperomierza)

Błąd pomiaru odchylenia toru elektronowego
wynosi 1mm.

Błąd powstały przy obliczaniu ładunku właściwego elektronu obliczam wykorzystując metodę różniczki zupełnej. Dla przejrzystości obliczeń podstawiam
= a

Więc: C =

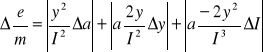
Przy czym: ∆y = 0,1 [cm] = 0,001 [mm] ∆I = 0,1 [mA] = 0,0001 [A]

Pomiary:

I[mA]	Polaryzacja dod. [cm]	Polaryzacja ujemna [cm]	wart y [m]	y*y	i*i	e/m=k*y*y/i*i [C/kg]
141,1	18,8	5,2	0,068	0,004624	0,01990921	192771084337,35
129,3	18,1	5,9	0,061	0,003721	0,01671849	184731396196,67
117,3	17,5	7,5	0,05	0,0025	0,01375929	150807200080,82
105,4	16,8	7,1	0,0485	0,00235225	0,01110916	175743935635,10
93,8	16,2	7,7	0,0425	0,00180625	0,00879844	170392421838,42
82,5	15,6	8,3	0,0365	0,00133225	0,00680625	162463544536,27
70,3	15,1	8,9	0,031	0,000961	0,022801	34982237621,16
58,6	14,5	9,4	0,0255	0,00065025	0,021025	25669797859,69
46,6	14	9,9	0,0205	0,00042025	0,00217156	160625310836,45
35	13,5	10,5	0,015	0,000225	0,001225	152448979591,84
23,4	13	11	0,01	0,0001	0,00054756	151581561837,97

Wynik ostateczny:

Wnioski:

Wyznaczona wartość stosunku e/m jest zbliżona do wartości tablicowej, która wynosi 1,76*10¹¹ C/kg. Błąd może być spowodowany dużą niedokładnością pomiaru odchylenia.

---