Podczas przeprowadzania ćwiczenia skorzystałem z następujących zależności.

-określenie poziomu domieszkowego E:

gdzie: a oznacza współczynnik nachylenia prostej ln(1/R)=f(1/T);

k oznacza stałą Boltzmana: k=1,38006210^-23 [J/K]

oraz 1 [J]=1,602189210^-19 [eV]

-błąd wyznaczenia poziomu domieszkowego E za pomocą różniczki logarytmicznej:

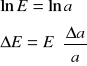
-określenie współczynnika nachylenia wykresu ln(1/R)=f(1/T) za pomocą regresji liniowej:

podczas analizy wyników i wykonywania obliczeń posłużyłem się programem „STATIST”, służącym do obliczania współczynnika nachylenia wykresu za pomocą regresji liniowej.

Na podstawie przedstawionych w punkcie 2. wzorów oraz wartości obliczonych podczas przeprowadzania ćwiczenia, zestawionych w tabeli 3., dokonałem niezbędnych obliczeń:

a)obliczanie wartości (wraz z błędem) współczynnika nachylenia wykresu ln(1/R)=f(1/T) (dane - dwie ostatnie kolumny tabeli 3.):

za pomocą programu „STATIST” dokonałem obliczeń wartości współczynnika nachylenia wykresu ln(1/R)=f(1/T) i otrzymałem następujący wynik:

• -3750  94

1. obliczanie wartości poziomu domieszkowego E (dane - współczynnik obliczony w punkcie 4.a.):

skoro wiadomo, że 1 [J]=1,602189210^-19 [eV] to 1,03510^-19 [J]=0,64602 [eV]

2. obliczanie błędu poziomu domieszkowego E (dane - wartość poziomu domieszkowego obliczona w punkcie 4.b.):

3. zestawienie wyniku poziomu domieszkowego z wartością jego błędu:

(0,6460,017) [eV]

Błąd pomiaru rezystancji mostkiem Wheatstone'a : R=0.1

Błąd pomiaru temperatury : T=1C

Współczynnik nachylenia prostej ln(1/R)=f(1/T) obliczony metodą regresji wynosi :

a= -63.890

a= -6.428

Poziom domieszkowy będzie zatem równy :

Błąd wyznaczenia poziomu domieszkowego :