Nr Ćw. 302	Data 8.03.2001	Krzysztof Gałęcki		Wydział Elektryczny			Semestr II	Grupa E-9
Prowadzący: Jarosław Gutek			przygotowanie		wykonanie	opracowanie		Ocena

Temat: Wyznaczanie stałej siatki dyfrakcyjnej

1. Falowy charakter światła.

Światło jest falą elektromagnetyczną rozchodzącą się w próżni ze stałą prędkością c. Jest rozchodzącym się w przestrzeni zaburzeniem pola elektromagnetycznego. Do celów optycznych potrzebne jest jedynie opisanie w czasie wektora elektryczengo fali świetlnej równaniem (dla fali biegnącej w kierunku osi x) :

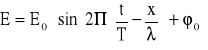
2. Zasada Hyghensa.

Jest ona oparta na konstrukcji geometrycznej i nie daje tak pełnego obrazu jak elektromagnetyczna teoria Maxwella. Brzmi ona: każdy punkt, który fala napotyka na swojej drodze staje się źródłem nowej fali kulistej; położenie fali można odczytać jako styczną do fal cząstkowych. Jest to podstawa wyjaśnienia zjawisk dyfrakcji i interferencji.

3. Interferencja.

Jest to wzajemne nakładanie się fal. W określonym punkcie przestrzeni nastapi wzmocnienie lub wygaszenie amplitudy w zależności od faz fal w tym punkcie.

a) Warunkiem na wygaszenie się wzjamne dwóch fal jest odwrotność ich faz, czyli różnica odległości od źródeł musi być równa połowie wielokrotności długości fali.

b) Warunek zaś konieczny do wzmocnienia się dwóch fal to zgodność ich faz, czyli różnica odległości od żródeł musi być równa całkowitej wielokrotności długości fali.

Chociaż interferencja zachodzi dla dowolnych fal to stały w czasie obraz interferncyjny można zaobserwować jedynie dla fal spójnych (koherentnych) - o stałej w czasie róznicy faz.

4. Dyfrakcja.

Jest to zjawisko ugięcia się fali zauważalne, gdy przechodzi ona przez szczelinę szczelinę o niewielkich rozmiarach.

dla a=10

a

dla a=

a

Zachowanie się fali za szczeliną zależy od szerokości tej szczeliny (a) w stosunku do długości fali (). Gdy a>> (pierwszy rysunek) szerokość przechodzącej wiązki jest w zasadzie równa szerokości otworu - oświetlenie ekranu , ustawionego równolegle do przeszkody jest obrazem geometrycznym otworu. W tej sytuacji zjawisko dyfrakcji praktycznie nie jest widoczne.Jeżeli jednak a<=: wówczas fala za szczeliną jest wyraźnie kulista i oświetla powierzchnię ekranu wielokrotnie większą od powierzchni szczeliny. Ten przypadek przedstawia zjawisko dyfrakcji (ugięcia) fali na pojedyńczej szczelinie.

5. Siatka dyfrakcyjna.

Jest to układ szczelin wzajemnie równoległych i leżących w stałej odległości. Wykonuje się je przez nacięcie rowków na szkle lub metalowej płycie za pomocą ostrza diamentowego. Maksimum główne to obszar największego podświetlenia w środkowej części widma ograniczony wystąpieniem pierwszego minimum lub wystąpieniem maksimów wtórnych, których natężenie jest bardzo małe. Jego szerokość jest wyznaczona przez położenie pierwszego minimum, aopisana jest wzorem:

, gdzie:

W siatkach dyfrakcyjnych szerokość szczelin jest rzędu długości fali świetlnej, więc natężenie prążków interferencyjnych jest prawie stałe.

6. Zdolność rozdzielcza.

Siatka dyfrakcyjna ma zdolność rozdzielczą R zdefiniowaną przez:

, gdzie:

jest średnią długości fali dwóch linii widmowych ledwie rozróżnialnych, a jest różnicą długości fal między nimi.

7. Kryterium Rayleigh'a.

Głosi ono, że dwa maksima są ledwie rozróżnialne, gdy ich odległość kątowa jest taka, że maksimum jednej linii przypada na minimum drugiej. Jeśli zastosujemy to kryterium, to możemy pokazać, że :

R=Nm, gdzie:

R--zdolność rozdzielcza, N--całkowita liczba nacięć, m--rząd obserwowanego widma.

8. Zasada pomiaru.

W celu znalezienia stałej siatki dyfrakcyjnej d (czyli odległości między środkami dwóch sąsiednich szczelin) skorzystamy z równania:

, gdzie:

n--rząd obserwowanego widma, --długość fali (dla lampy sodowej =589,3 nm), --kąt pod jakim obserwowane jest max. widma.

Wartości kątów dla poszczególnych rzędów n odczytujemy za pomocą spektrometru zaopatrzonego w dokładną podziałkę kątową. Rozbieżne światło lampy sodowej wpada do kolimatora przez szczelinę umieszczoną w ognisku soczewki, przez co opuszcza go jako wiązka równoległa. Następnie pada na siatkę dyfrakcyjną zamontowaną na osi obrotu lunetki z soczewką skupiającą. Lunetka jest trwale połaczona z kątomierzem, zatem jej położenie można z dużą dokładnością odczytywać ze skali kątowej zaopatrzonej w noniusz.

9. Wyniki pomiarów.

SIATKA A
	Położenie prążka rzędu 0.	Odchylenie prążka rzędu 1.		Odchylenie prążka rzędu 2.		Odchylenie prążka rzędu 3.
L.p.		w lewo	w prawo	w lewo	w prawo	w lewo	w prawo
1	142,2500°	6,8330°	6,7500°	13,6999°	13,6336°	20,8831°	20,8502°
2	142,2500°	6,8497°	6,7667°	13,7500°	13,6253°	20,8914°	20,8836°
3	142,2667°	6,8580°	6,8168°	13,7650°	13,6503°	20,8664°	20,8168°
SIATKA B
1	142,2500°	16,9165°	17,3001°	35,1331°	37,0167°	Nie dało się zaobserwować prążków 3-go rzędu.
2	142,2500°	16,9332°	17,3168°	35,1414°	37,0000°
3	142,2667°	16,9415°	17,3085°	35,1331°	36,9666°

10. Obliczenia i rachunek błędów.

Zgodnie z poleceniem w skrypcie obliczam wartość stałej siatki dla każdego z dokonanych

pomiarów (korzystając z wzoru w pkt. 8) otrzymując, po zaokrągleniu do 2 miejsc po przecinku następujące wyniki :

SIATKA A
	Stała liczona względem prążka rzędu 1.				Stała liczona względem prążka rzędu 2.		Stała liczona względem prążka rzędu 3.
L.p.	w lewo	w prawo			w lewo	w prawo	w lewo	w prawo
1	4953,11	5013,72			4976,43	5000,16	4959,57	4967,05
2	4941,09	5001,41			4958,65	5003,15	4957,69	4959,46
3	4935,14	4964,82			4953,35	4994,17	4963,36	4974,66
śr.	4943,11	4993,32			4962,81	4999,16	4960,21	4967,06
średnia stała siatki A:			(4970,95 ± 8,69) nm
SIATKA B
1	2025,24	1981,66			2048,04	1957,65	Nie dało się zaobserwować prążków 3-go rzędu.
2	2023,30	1979,81			2047,62	1958,41
3	2022,34	1980,73			2048,04	1959,93
śr.	2023,63	1980,73			2047,90	1958,66
średnia stała siatki B:			(2009,48 ± 20,59) nm

11. Wnioski i uwagi.

Otrzymane wyniki pozwalają obliczyć ilość rys przypadającą na cm dla badanej siatki. Wynosi ona około 2011 rys/cm dla siatki A i około 4976 rys/cm dla siatki B. Podsumowując, pomiary nie odbiegały od siebie za bardzo ze względu na zastosowanie noniusza przy mierzeniu kąta odchylenia, co zdecydowanie zwiększało dokładność pomiaru. W ćwiczeniu możnaby użyć kilku różnych lamp dających światła o różnych długościach fali.

---