Aproksymacja

Grzegorz Hoppe

Robert Watras

Zadaniem aproksymacji funkcji jest znalezienie funkcji która jest przybliżeniem funkcji dokładnej w ściśle sprecyzowanym sensie. W przypadku poniższego zadania staramy się znaleźć funkcję analityczną (wielomianową), która będzie przybliżeniem funkcji określonej dyskretnie (ciągu wyników pomiaru). Sprawdzimy jak zależy dokładność aproksymacji od stopnia wielomianu aproksymującego.

Do znalezienia współczynników wielomianu posłuży nam następujący algorytm:

Jeżeli punktu pomiarowe pogrupujemy w tabeli pomiarowej w postaci tablicy

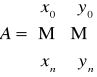
gdzie

to współczynniki wielomiany aproksymującego wyznaczymy rozwiązując następujące równanie macierzowe

gdzie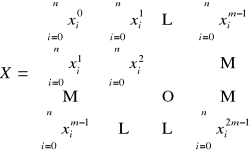
,
.

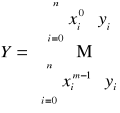
Otrzymana macierz

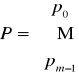
będzie macierzą współczynników wielomianu aproksymującego

Do wykonania tego zadania posłużył nam program napisany w matlabie. Poniżej przedstawiliśmy fragment kodu źródłowego odpowiedzialnego za obliczenie współczynników wielomianu.

ax=input('Podaj macierz Ax ');

ay=input('Podaj macierz Ay ');

m=input('Podaj rząd wielomianu ');

m=m+1;

[n,n]=size(ax);

x=repmat(0,[m,m]);

for w=1:m

for k=1:m

for i=1:n

x(k,w)=x(k,w)+ax(i)^(k+w-2);

end

end

end

x

y=repmat(0,[m,1]);

for w=1:m

for i=1:n

y(w,1)=y(w,1)+(ax(i)^(w-1))*ay(i);

end

end

y

p=x\y

Otrzymane wielomiany przedstawiliśmy na wykresach. W zależności od narzuconego przez nas stopnia m wielomianu W otrzymaliśmy wykresy, mniejszym lub większym stopniu, odzwierciedlające wyniki przeprowadzonego hipotetycznie doświadczenia. W naszym sprawozdaniu umieściliśmy wyniki dwóch serii aproksymacji wielomianami o stopniach 0-6 dla podpunktów

c)
e)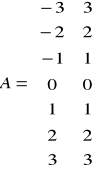

Dla każdej aproksymacji obliczyliśmy średni błąd względny w poszczególnych punktach. Następnie przedstawiliśmy na wykresie zależność błędu od stopnia wielomianu aproksymującego.

Jak wywnioskowaliśmy z powyższych wykresów aproksymacja funkcją wielomianową jest tym lepsza (dokładniejsza) im większy jest stopień tego wielomianu. Jednak w niektórych przypadkach okazuje się uzasadniona aproksymacja nawet do funkcji liniowej. Na przykład wtedy gdy wiemy że zmienność wyników powinna mieć charakter liniowy ale wyniki są obarczone błędem.

Ponadto zauważyliśmy, że w przykładzie e) zmiana stopnia wielomianu z parzystego na nieparzysty nie przyniosła poprawy dokładności. Okazało się, że zwiększenie stopnia wielomianu, w tych przypadkach, nie wpłynęło na współczynniki wielomianu a jedynie dodała jeden współczynnik równy 0. Jest to według nas spowodowane, tym że wyniki pomiarów mają charakter funkcji parzystej.

---