Kowalik Artur GR.3.3 data wykonanie ćwiczenia;

29,10,1999'

ĆWICZENIE 2.2

WYZNACZANIE OKRESU DRGAŃ WŁADNYCH GALWANOMETRU.

1.WYKONAIE ĆWICZENIA;

W celu wykonania drgań własnych galwanometru zestawiamy obwód według schematu podanego na rysunku zamieszczonym poniżej. Do tego celu używamy galwanometru zwierciadłowego przenośnego o oporze właściwym R_g=184Ω i oporze krytycznym R_kg=2350Ω.

Ustawiamy następnie wartość oporów R₂=10000Ω oraz R=R_kg-(R_g+R₁) oraz R₁ tak, aby przy podanej wartości napięcia U₀=20mV wskaźnik galwanometru wychylił się do końca skali. Uwzględniając, że wartość R₁<<R_g na oporniku R można ustawić wartość R=R_{kr ­­}-R_g co w naszym przypadku odpowiada wartości;

R=2350Ω.-184Ω=2166Ω

Zwiększenie oporu R­₁ dokonujemy przy zamkniętych wyłącznikach W­₁ i W₂ oraz przy otwartym wyłączniku W₃. Po otwarciu wyłącznika W₂ zauważamy, że wskaźnik świetlny galwanometru zaczyna wahać się wokół `'zera'' galwanometru. Otwierając wyłącznik W₂ jednocześnie włączamy sekundomierz i mierzymy czas 20,25 i 30 wahnięć.

Okres drgań własnych galwanometru określamy na podstawie wzoru;

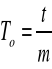
gdzie ``t'' jest zmierzonym czasem wahań, a `'m'' liczbą wahań. Pomiary okresu drgań własnych galwanometru przeprowadzamy odpowiedni dziesęcio-, pięcio- oraz sześciokrotnie.

2. WYNIKI POMIARÓW;

l.p.	m.	t	T0	Rk
1	20	29,59	1,4795	2350
2	20	29,51	1,4755	2350
3	20	29,65	1,4825	2350
4	20	29,5	1,475	2350
5	20	29,61	1,4805	2350
6	20	29,4	1,47	2350
7	20	29,53	1,4765	2350
8	20	29,58	1,479	2350
9	20	29,43	1,4715	2350
10	20	29,59	1,4795	2350
11	25	36,99	1,4796	2350
12	25	36,78	1,4712	2350
13	25	36,85	1,474	2350
14	25	36,9	1,476	2350
15	25	36,95	1,478	2350
16	25	36,98	1,4792	2350
17	30	44,38	1,4793333	2350
18	30	44,27	1,4756667	2350
19	30	44,35	1,4783333	2350
20	30	44,3	1,4766667	2350
21	30	44,32	1,4773333	2350
wartości średnie	23,80952	35,16476	1,4768968	2350

3.ANALIZA BŁĘDU;

Zostanie przeprowadzona metodą Gaussa, dlatego aby wyznaczyć błąd pomiaru okresu drgań własnych T_o obliczamy; --> [Author:A.K.]

• Średnią arytmetyczną wyników pomiaru

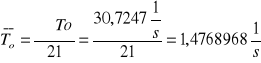
• Błędy pozorne (residua) dla poszczególnych pomiarów (wszystkie wyniki pomiarów umieszczamy w tabeli)

• Kwadraty błędów pozornych i ich sumy r_To² oraz ∑ r_To²

• Średni błąd kwadratowy pojedynczego pomiaru (odchylenie standardowe)

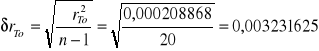
• Średni błąd kwadratowy średniej arytmetycznej, który w przypadku pomiarów jest całkowitym błędem pomiaru danej wielkości;

T0	rto	rto^2	Σ rto^2
1,4795	0,002593651	6,72702E-06	0,000208868
1,4755	-0,001406349	1,97782E-06	0,000208868
1,4825	0,005593651	3,12889E-05	0,000208868
1,475	-0,001906349	3,63417E-06	0,000208868
1,4805	0,003593651	1,29143E-05	0,000208868
1,47	-0,006906349	4,76977E-05	0,000208868
1,4765	-0,000406349	1,6512E-07	0,000208868
1,479	0,002093651	4,38337E-06	0,000208868
1,4715	-0,005406349	2,92286E-05	0,000208868
1,4795	0,002593651	6,72702E-06	0,000208868
1,4796	0,002693651	7,25575E-06	0,000208868
1,4712	-0,005706349	3,25624E-05	0,000208868
1,4742	-0,002706349	7,32433E-06	0,000208868
1,476	-0,000906349	8,21469E-07	0,000208868
1,478	0,001093651	1,19607E-06	0,000208868
1,4792	0,002293651	5,26083E-06	0,000208868
1,4793333	0,002426984	5,89025E-06	0,000208868
1,4756667	-0,001239683	1,53681E-06	0,000208868
1,4783333	0,001426984	2,03628E-06	0,000208868
1,4766667	-0,000239683	5,74477E-08	0,000208868
1,4773333	0,000426984	1,82315E-07	0,000208868
1,4769063

Zestawienie analizy błędów pomiarów w tabeli:

Wynik pomiaru zapisujemy w postaci zapisu błędu za pomocą kryterium jednosigmowego;

Stąd wniosek, że otrzymaną wartość okresu drgań możemy zapisać za pomocą przedziału w następujący sposób;

Oznacza to, że w tym przedziale można z dużym prawdopodobieństwem oczekiwać wartości rzeczywistej.

Stąd możemy obliczyć procentową wartość błędu;

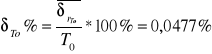
4. WNIOSKI;

Doświadczenie miało na celu wykazanie drgań własnych galwanometru. Pomiar wykazał wynik pomiaru na poziomie 1,4769063 wahnięć na sekundę. Pamiętać jednak musimy, że pomiar jest obarczony jest błędem, analiza błędu wykazała odchylenie pomiaru rzędu 0,0477%. Błąd na tym poziomie można by uznać za niewielki, niemniej jednak musimy zwrócić uwagę na wielkość mierzoną, w tym przypadku sekundę. --> [Author:A.K.] W przypadku, gdy mielibyśmy wielkość większą, błąd tego rzędu okazałby się znaczącym.

Odchylenie równe 0,0477% można wytłumaczyć liczbą pomiarów, gdyż wraz ze wzrostem tej liczby maleje błąd pomiaru, co wynika z odpowiednich reguł statystycznych.

Przy wykonaniu tego ćwiczenie nie możemy zapominać o możliwości zwiększenia dokładności pomiaru. Zastosowanie większej liczby pomiarów pozwoliłoby na uzyskanie bardziej optymalnego wyniku okresu drgań własnych galwanometru.

1

G

R₂

R

R₁

V

We DN Wy

---