7. Podstawowe właściwości przekształcenia Fouriera.

- twierdzenie o przesunięciu w dziedzinie częstotliwości (tw. o modulacji)

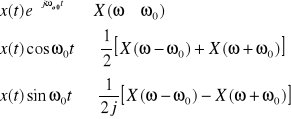
- twierdzenie o podobieństwie (o zmianie skali)

- twierdzenie o splocie w dziedzinie czasu

- twierdzenie o splocie w dziedzinie częstotliwości

- twierdzenie o energii (Parsevala)

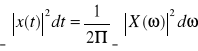
- twierdzenie o różniczkowaniu w dziedzinie czasu

- twierdzenie o funkcji korelacji wzajemnej

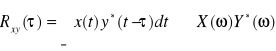
19. Stacjonarność sygnałów stochastycznych

Sygnały losowe stacjonarne:

- stacjonarne całkowicie (w ścisłym, węższym sensie)

- stacjonarne rzędu n

- słabo stacjonarne (w szerokim sensie)

• Sygnał losowy jest stacjonarny całkowicie jeśli dowolna łączna n-wymiarowa łączna funkcja gęstości prawdopodobieństwa jest niezmienna względem przesunięcia τ' w czasie

łączna n-wymiarowa funkcja gęstości prawdopodobieństwa w przekrojach
jest taka sama jak w przekrojach
, dla każdej liczby naturalnej n i dla każdej liczby rzeczywistej τ'

• Sygnał losowy jest stacjonarny rzędu n jeśli łączna n-wymiarowa łączna funkcja gęstości prawdopodobieństwa jest niezmienna względem przesunięcia τ' w czasie

(nie wymaga spełnienia warunku dla każdego n)

jeżeli sygnał jest stacjonarny rzędu n, to jest również stacjonarny rzędu k, dla każdego

• Sygnał losowy
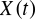
  jest słabo stacjonarny jeśli jego wartość średnia i wariancja nie zależą od czasu a funkcja autokorelacji (autokowariancji) zależy tylko od odstępu między przekrojami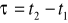
  :

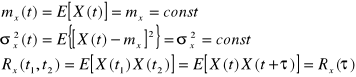
1

---