Wykłady z ekonometrii

rok akademicki 2002/2003

2. Klasyczny model regresji liniowej.

Regresja w statystyce jest terminem oznaczającym metody modelowania związków między zmiennymi. Termin regresja został wprowadzony pod koniec dziewiętnastego wieku przez Francisa Galtona. W jednej ze swoich prac ogłosił on wyniki badań związku między wzrostem ojców i ich synów. Do par punktów reprezentujących wzrost syna i ojca dopasował linię prostą. Odnalazł on własność, którą nazwał "powracaniem do przeciętności" (regression to mediocrity): wzrost synów wykazywał odchylenia od wzrostu ojców w kierunku wzrostu przeciętnego.

W pierwszej części wykładu ograniczymy się w zasadzie do rozważania tzw. klasycznego modelu regresji liniowej.

Szukamy związku pomiędzy zmienną y, a zbiorem k zmiennych
. Terminologia: y - zmienna objaśniana (regresant),
- zmienne objaśniające (regresory). Klasyczny model regresji liniowej otrzymujemy, gdy przyjmiemy następujące założenia:

Założenie 1. Model jest liniowy względem parametrów, tzn. zmiana wartości danej zmiennej objaśniającej powoduje proporcjonalną zmianę zmiennej objaśnianej:

,

gdzie

• 
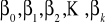
  są parametrami modelu (nieznanymi na ogół liczbami rzeczywistymi),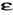

• 
  jest składnikiem losowym (błędem).

Przeprowadzamy n obserwacji zmiennej objaśnianej y. Można je zapisać w postaci

,

,

..................................................................

,

gdzie

• 
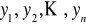
  są obserwacjami zmiennej objaśnianej y

• 
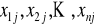
  są wartościami zmiennej objaśniającej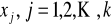
  .

Powyższy układ równań nazywamy modelem liniowej regresji wielu zmiennych lub modelem regresji wielorakiej ( wielokrotnej).

Założenie 2. Dla każdej obserwacji składnik (błąd) losowy ma rozkład normalny o średniej równej zeru i nieznanym odchyleniu standardowym
oraz jest niezależny od składników losowych pozostałych obserwacji. Oznacza to, że
są niezależnymi zmiennymi losowymi o jednakowym rozkładzie normalnym
.

Założenie 3. Wartości
,
, są ustalane (nielosowe). Jedynym źródłem losowości zmiennej objaśnianej y jest składnik losowy
.

W powyższej sytuacji wygodnie jest wykorzystywać zapis macierzowy. Pozwoli to istotnie uprościć wzory występujące w teorii regresji. Pojęcie i własności macierzy są podstawowym elementem wstępnych wykładów z algebry. Wprowadźmy oznaczenia:

• macierz wymiaru
  

,

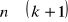
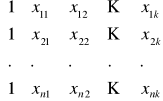
• wektory kolumnowe

,

,

.

Model regresji liniowej zapisujemy krótko

.

Podamy dwa przykłady danych do opracowania których wykorzystamy klasyczny model regresji liniowej

Przykład 2.1 (Inflacja 2000). Dane dotyczące inflacji w Polsce w pierwszych dziewięciu miesiącach przedstawiały się następująco:

Miesiąc	1	2	3	4	5	6	7	8	9
Inflacja (w %) y	1,8	2,7	3,6	4,0	4,7	5,5	6,2	5,9	6,9

W tym przypadku

,

,

,

.

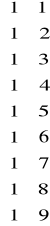
Przykład 2.2 (Reklama). Pewna firma nasiliła kampanię promocji swoich wyrobów. Oprócz reklam radiowych i telewizyjnych zorganizowała pokazy działania swoich produktów w sklepach. W ciągu 10 tygodni śledzono wydatki na reklamę telewizyjną i radiową (
), wydatki na pokazy w sklepach (
) oraz wielkość tygodniowej sprzedaży (
). Poniżej w tabeli przedstawione są obserwacje (dane w tys. $).

72	12	5
76	11	8
78	15	6
70	10	5
68	11	3
80	16	9
82	14	12
65	8	4
62	8	3
90	18	10

Zauważmy, że teraz

,

,

,

.

1

4

---