a) obliczenie współczynnika jeziorności
JEZ = ![]()
b) obliczenie współczynnika zabagnienia
B=![]()
c) obliczenie współczynnika redukcji jeziornej
δj = ![]()
d) oblicznie współczynnika redukcji bagiennej
δB = ![]()
Jeżeli B<0,20 to δB = 1
e) przepływ jednoprocentowy
![]()
[m3/s]
f) przepływ miarodajny Qm = Q1% * λp ![]()
g) promień hydrauliczny Rh=A/U
h) moduł przepływu K=A*1/n*Rh^2/3
ŚWIATŁO MOSTU
![]()
![]()
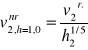
odczytujemy z tablic grunt I lambde
![]()
![]()
MODEL PRZEPŁYWU WOLNOZMIENNEGO
Wykonując te obliczenia sprawdzono prawdziwą rzędną zwierciadła wody, gdyż przepływ rzeki jest w rzeczywistości wolnozmienny, a nie jednostajny jak do tej pory założono w poszczególnych obliczeniach.
If - spadek linii energii
hc - strata linii energii całkowitej
I - spadek zwierciadła wody
![]()
- wysokość prędkości dla danego przekroju
![]()
- współczynnik Saint-Venanta dla danego przekroju
Równanie energetyczne - wysokość energii całkowitej dla danego przekroju:
![]()
![]()
![]()
![]()
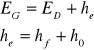
Gdzie:
hf - straty energii wynikające z tarcia strumienia o ściany i dno koryta
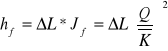
![]()
- odległość między przekrojami A i B
h0 - straty energii wynikające z deformacji strumienia przy przepływie przez przeszkody (straty lokalne)
Ce - współczynnik strat wynikających z deformacji strumienia
Ce = 0,5 - dla rozszerzenia strumienia za mostem
Ce = 0 - dla odcinka pod mostem
Ce = 0,3 - dla zwężenia strumienia przed mostem
![]()
![]()
- szukany poziom zwierciadła wody dla danego przekroju
Dla pierwszego przybliżenia zakładamy, że:
a) ![]()
b) KG = KD
c) h0 = 0
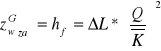
Obliczenia przeprowadza metodą iteracyjną (kolejnych przybliżeń) dotąd, aż zostaną spełnione warunki:
![]()
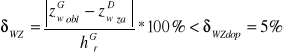
ROZMYCIE POD FILAREM
![]()
6.2.1. Współczynnik kształtu filaru K1, wg tabeli 4.6 [4]
Prędkość w przekroju ![]()
6.2.4. Współczynnik szorstkości zastępczej
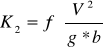
Współczynnik K3 ![]()
h - wysokość wody przy filarze
b - szerokość zastępcza filara
rozkładu prędkości dla głębokości przybrzeżnych
α = 1,0 - filar usytuowany na terenie zalewowym
Współczynnik charakteryzujący podłoże
c = 30*d90
Równanie Maninga:
![]()
v - średnia v
n - współczynnik szorstkości wg. Maninga
i - spadek hydrauliczny równy spadkowi dna kanału
Przepływ jednostajny - przepływ, którego parametry nie zmieniają się w czasie, w przekroju strumienia cieczy i jego przekroje też się nie zmieniają. Istnieje swobodna powierzchnia cieczy, na którą wywierane jest ciśnienie atmosferyczne. Odbywa się w kanałach o przekroju otwartym (kanały o przekroju prostokątnym lub trapezowym) lub zmkniętym (kanały o przekroju kołowym lub gruszkowym)
Przepływ miarodajny - przepływ maksymalny prawdopodobny o określonym prawdopodobieństwie p.
- przepływ, który średnio statystycznie będzie osiągnięty lub przekroczony raz na T lat
- przepływ równy maksymalnemu przepływowi rocznemu o prawdopodobieństwie przekroczenia równym p
Przepływ zmienny - przepływ, którego parametry zmieniają się w czasie i jego przekroje też się zmieniają. Jeżeli warunki przepływu zmieniają się nieznacznie, przepływ nosi nazwę przepływu wolnozmiennego.
Ruch wolnozmienny - ustalony przepływ w korycie pryzmatycznym, w którym zwierciadło cieczy nie jest równoległe do dna koryta. Ruch ten występuje najczęściej w korycie naturalnym lub zabudowanym (np. zapora). Jeżeli różnice głębokości cieczy na pewnym odcinku są nieznaczne, ruch ten nazywamy wolnozmiennym. Cząsteczki cieczy poruszają się prawie po liniach prostych, a przekroje poprzeczne strumienia zmieniają się tak wolno, że wektory prędkości można przyjmować jako prostopadłe do przekroju.
Ruch szybkozmienny - charakteryzuje się znacznymi różnicami głębokości w położonych blisko siebie przekrojach. Nie są spełnione założenia dotyczące modelu przepływu jednowymiarowego.
Ruch krytyczny - ruch, w którym dla danego natężenia przepływu energia strumienia jest minimalna. Ruch krytyczny stanowi granicę między przepływami spokojnymi i rwącymi.
Ruch rwący (podkrytyczny) - ruch, w którym prędkość i spadek są większe od krytycznego, a głębokość średnia mniejsza od głębokości krytycznej.
Ruch spokojny (nadkrytyczny) - ruch, w którym prędkość i spadek są większe od krytycznych, a głębokość większa od krytycznej.
Głębokość krytyczna - hkr - strumienia cieczy jest to głębokość
przy, której osiąga on minimum energii całkowitej.
Równanie Bernoulliego - bilans energetyczny cieczy doskonałej. Suma trzech wartości - wysokości prędkości, ciśnienia piezometrycznego, położenia środka ciężkości pola przekroju poprzecznego strugi.
![]()
y1 - wysokość środka ciężkości
p1/γ - wartość ciśnienia piezometrycznego
v2/2g - wysokość prędkości
Światło mostu zależy od prędkości nierozmywalnej.
Prędkość nierozmywalna zależy od rodzaju gruntu.
Obliczenia hydrologiczne - do ustalania poziomu wód, prędkości oraz objętości przepływu miarodajnej wielkiej wody.
Obliczenia hydrauliczne - służą do wyznaczania wielkości pozwalających na zaprojektowanie przeprawy mostowej o odpowiednich wymiarach, które zagwarantują efektywny przepływ wody, nie zagrażający obiektowi ani przyległym terenom, dającej możliwość efektywnej eksploatacji przestrzeni podmostowej.
Metody wyznaczania przepływu maksymalnego prawdopodobnego Qp
a) metody bezpośrednie - bazują na analizie statystycznej wyników pomiarów hydrometrycznych przepływów maksymalnych rocznych.
b) metody pośrednie - w przypadku braku danych hydrometrycznych
- metody genetyczne - bazują na równaniach opisujących proces fizyczny, proces transformacji opadów w odpływ
*genetyczna formuła opadowa - stosowana do zlewnie mniejszych od 50km2. Możliwość stosowania dla całej Polski.
*metoda roztopowa - opisuje transformacje roztopu śniegu w odpływ. Zalecane dla zlewni większych od 50km2. Polska środkowa i północna.
![]()
Wyszukiwarka
Podobne podstrony:
386 387
387%20mensile
387
387
387
387
387-1
29 387 402 HSS Produced by Conventional Casting, Spray Forming and PM
387 392 id 36434 Nieznany
387 Manuskrypt przetrwania
387
383 387
387
387
387
387
387
więcej podobnych podstron