W życiu codziennym drgania występują bardzo często. Najłatwiej

jest badać i opisywać drgania wahadła lub ciała zawieszonego na sprężynie - w poziomie lub pionie (ruch drgający). Graficznie ruch drgający przedstawiamy w układzie współrzędnych. Obrazem tego ruchu jest sinusoida (zależność wychylenia od czasu trwania ruchu).

Podstawowe pojęcia niezbędne do opisu ruchu drgającego:

Położenie równowagi - położenie ciała przed wprowadzeniem go w ruch drgający.

Wychylenie -odległość ciała od położenia równowagi w pewnej chwili,

symbol - x, jednostka [1 m].

Amplituda - maksymalne wychylenie od stanu równowagi, symbol - A, jednostka [1 m].

Okres drgań - czas jednego, pełnego drgania, jednostka - T, symbol [1s].

Częstotliwość drgań - liczba drgań w jednej sekundzie, symbol - ν, jednostka [1/s].

Ruch harmoniczny - ruch drgający, w którym pomijamy opory. Amplituda drgań jest stała.

Cechy ruchu harmonicznego:

• ruch powtarzający się, czyli okresowy;

• prędkość ciała drgającego ulega zmianie (zmienia się również wartość i zwrot prędkości);

• w położeniach maksymalnego wychylenia prędkość ciała wynosi zero;

• przy przechodzeniu przez położenie równowagi ciało ma maksymalną szybkość;

• ciało porusza się ruchem przyspieszonym gdy zbliża się do położenia równowagi;

• ciało porusza się ruchem opóźnionym gdy oddala się od położenia równowagi;

• ruch ciała jest ruchem niejednostajnie zmiennym.

Oscylator harmoniczny - jest to ciało, wykonujące drgania harmoniczne.

Okres drgań własnych - okres drgań wahadła wychylonego o bardzo mały kąt, ciało wykonuje drgania o nie zmieniającym się okresie.

Częstotliwość drgań własnych - odwrotność okresu drgań własnych.

Drgania wymuszone - drgania ciała wywołane przez zewnętrzną siłę, której wartość zmienia się okresowo. Mają taka samą częstotliwość jak siła zewnętrzna wymuszająca te drgania.

Rezonans - wzbudzenie do drgań ciała przez inne drgające ciało.

Częstotliwość rezonansowa - jest to częstotliwość wymuszająca drgania rezonansowe.

Wahadło matematyczne - kulka o małych rozmiarach zawieszona na nieważkiej i nierozciągliwej nici.

PODSTAWOWE WZORY DOTYCZĄCE RUCHU DRGAJĄCEGO

1. F_s= kx

F_s - siła sprężystości;

k - współczynnik proporcjonalności charakteryzujący własności sprężyste danej sprężyny

x - wychylenie

2. T = 2π
   

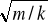
T - okres drgań oscylatora harmonicznego;

m - masa drgającego ciała;

3. W_z = ΔE_p = ½ kx²

W_z - praca siły zewnętrznej, która wprawia ciało w ruch drgający;

ΔE_p - przyrost energii potencjalnej

4. E_c = ½ kA²

Gdy wychylenie jest równe amplitudzie całkowita energia układu jest równa energii potencjalnej.

E_c - energia całkowita;

A - amplituda.

5. E_p = ½ kx²

E_p - energia potencjalna ciała drgającego wychylonego o x;

6. F = mg sinα lub F =
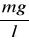
   x

F - siła wypadkowa działająca na wahadło matematyczne;

m - masa ciała zawieszonego na nici;

g - przyspieszenie ziemskie;

α - kąt wychylenia; dla małych katów sinα = x/l, gdzie l oznacza długość wahadła;

7. k =
   

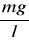
k - współczynnik proporcjonalności wahadła matematycznego;

8. T = 2π

Przykłady ciał drgających:

α Wahadło matematyczne

Na rysunku zaznaczono kąt wychylenia między

położeniem równowagi wahadła i wychyleniem

1. 2.

Przykłady oscylatorów harmonicznych

Rys. 1. Pionowe linie wyznaczają skrajne wychylenia ciała

Rys. 2. Poziome linie wyznaczają skrajne wychylenia ciała

x [m]

T t [s]

T

Obraz drgań ciała z pominięciem oporu (amplituda stała),

ruch harmoniczny.

Zadanie domowe

1. Co nazywamy izochronizmem? http://www.onet.pl/23b?q=izochronizm&k=ew

2. Praca z komputerem (dla chętnych): program 09 - wahadło matematyczne: http://www.zamkor.pl/

---