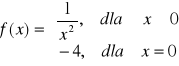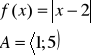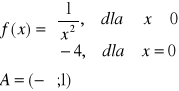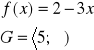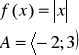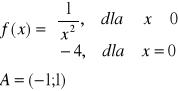Zadania MDC3 semestr zimowy 2010/2011

Zadanie 1. W zbiorze X * Y dana jest relacja R. Wyznaczyć wszystkie pary należące do tej relacji.

a) X = {Paryż. Monachium, Berlin}, Y = {Polska, Niemcy, Austria, Francja},
R = {(x, y): miasto x leży w państwie y}

b) X = {1,2,3}, Y = {6,7,8}, R = {(x, y) : x|y}

c) X=Y=N, R = {(x, y) : x² + y² ≤ 10}

d) X = {2,5,8,12}, Y = {3,4,10}, R = {(x, y): liczba x ma z liczbą y tylko jeden wspólny dzielnik!

Zadanie 2. W zbiorze X dana jest relacja R. Zbadać, czy ta relacja jest: 1) zwrotna, 2) symetryczna, 3) przechodnia. 4) relacją równoważności. Jeżeli dana relacja jest relacją równoważności, to wyznaczyć klasy abstrakcji tej relacji.

a) X - zbiór punktów na płaszczyźnie Oxy,

R = {(X, y): odległość punktu x od początku układu jest równa odległości punktu y od początku układu }

b) X - zbiór mieszkańców Polski.

R = {(x, y): x jest ojcem y)

c) X - zbiór mieszkańców Polski,

R = {(x, y): x jest przodkiem y}

d) X - zbiór miast w Polsce.

R = {(x, y): miasto x leży w tym samym województwie co miasto y}

e) X - zbiór wszystkich podzbiorów ustalonej płaszczyzny,

R = {(x, y) : x * y}

Zadanie 3. W zbiorze X dana jest relacja R. Zbadać, czy ta relacja jest: 1) zwrotna, 2) symetryczna, 3) przechodnia. 4) relacją równoważności. Jeżeli dana relacja jest relacją równoważności, to wyznaczyć klasy abstrakcji tej relacji.

a) X = R, R = {(x, y) : x < y) b) X = R, R = {(x, y) : x ≤ y} c) X = R, R = {(x, y) : |x| = |y|}

d) X = R, R = {(x, y) : xy > 0} e) X = R, R = {(x, y) : xy ≥ 0} f) X = R\{0}, R = {(x, y) : xy>0}

Zadanie 4. W zbiorze X ={a, b, c, d} dana jest relacja R. Sprawdzić, czy ta relacja jest: 1) zwrotna. 2) symetryczna. 3) przechodnia, 4) relacją równoważności.

Jeżeli dana relacja jest relacją równoważności, to wyznaczyć klasy abstrakcji tej relacji.

a) R= {(a, a), (b, b), (c, c), (d, d), (a, b), (b, a), (c, d), (d, c)}

b) R = {(a, a), (a, b), (b, a), (b, c), (c, b), (a, c), (c, a)},

c) R = {(a, a), (b, b), (c, c), (d, d)}

d) R = {(a, a), (b, b)}

e) R = {(a, a), (b, b), (c, c), (d, d), (a, b), (b, c)}

f) R = {(a, b), (a, c), (b, c), (b, d), (c, d), (d, d)}

Zadanie 5. W zbiorze X dana jest relacja R. Zbadać, czy ta relacja jest: 1) relacją porządku, 2) relacją liniowego porządku, 3) relacją dobrego porządku.

W przypadku gdy jest to relacja porządku, wyznaczyć elementy: maksymalny, minimalny, największy i najmniejszy (o ile takie istnieją).

a) X - zbiór przedziałów postaci (-a; a), gdzie a ∈ R₊ (zbiór liczb rzeczywistych dodatnich), R = {(x, y) : x * y}

b) X = Z, R = {{x, y) : |x| ≤ |y|}

c) X = R, R = {(x, y) : |x| < |y|}

d) X = N, R = {(x, y) : x|y ∨ x ≤ y}

e) X = N\{1}, R = {{x, y): x|y ∨ x ≤ y}

i) X - zbiór liczb postaci
gdzie n ∈ N , R = {(x, y): x ≤ y}.

Zadanie 6. Dany jest schemat relacji porządku. Wymienić elementy: maksymalny, minimalny, największy i najmniejszy (o ile takie istnieją). Wskazać wszystkie łańcuchy trójelementowe.

a) a → b → c ↓ ↓ d → e	b) a → b → c ↓ d → e → f	c) a → b → c → d e → f → g
d) a → b → c ↓ d → e → f	e) a → b → c ↓ ↑ d → e → f	e) a → b e → f ↓ ↑ c → d

Zadanie 7. W zbiorze X dana jest relacja porządku R = {(x, y) : x|y}. Narysować schemat tej relacji. Wymienić elementy: maksymalny, minimalny, największy i najmniejszy (o ile takie istnieją).

a) X = {2,3,5,6} b) X = {2,3,6,8} c) X = {2,3,6,12}

d) X = {2,6,10,12} e) X = {2,3,4,8,9,27} f) X = {2,3,4,9,36}

Zadanie 8. Przyjmujemy, że dziedziną każdej z podanych poniżej funkcji jest zbiór tych liczb rzeczywistych, dla których wzór określający tę funkcję ma sens. Wyznaczyć tę dziedzinę.

a)	b)	c)
d)	e)	f)

Zadanie 9. Dana jest funkcja f: R → R . Wyznaczyć przeciwdziedzinę (czyli zbiór wartości) tej funkcji.

a)

b)

c)

Zadanie 10. Dana jest funkcja f: R → R i zbiór A * R. Wyznaczyć obraz zbioru A w przekształceniu f.

a)

b)

c)

Zadanie 11. Wyznaczyć przeciwobrazobraz zbioru G w przekształceniu f: R → R określonym poniżej

a)

b)

c)

Zadanie 12. Sprawdzić czy dana funkcja jest: 1) różnowartościowa, 2) wzajemnie jednoznaczna.

a) f: N → N ∪ {0}, f(x) = x-1 b) f: Z → Z. f(x) = -x

c) f: <0;*) → <0;*), f(x) = x^2 k) f: R\{0} → R\{0}, f(x) =

Zadanie 13. Sprawdzić że funkcja g jest funkcją odwrotną do funkcji f.

a) f: R\{0} → R\{0}, f(x) = g: R\{0} → R\{0}, g(x) =

b) f: <0;*) → <0;*), f(x) = x^2 g: <0;*) → <0;*), g(x) =

Zadanie 14. Wyznaczyć funkcję złożoną g°f gdy

a) f: R\{0} → R\{0}, f(x) = g: R\{0} → R\{0}, g(x) =

b) f: R → R, f(x) = 2x+3, g: R → R, g(x) = 5

Zadanie 15. Podaj wzór funkcji booleowskiej odpowiadającej sieci logicznej pokazanej na rysunku

Zadanie 16. Naszkicuj sieci logiczne równoważne z sieciami pokazanymi na rysunku, ale składające się wyłącznie z bramek NAND.

---